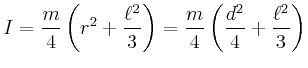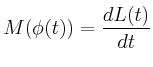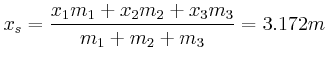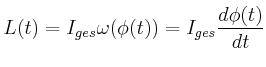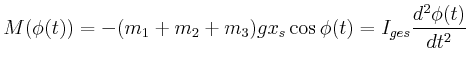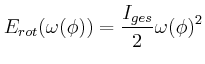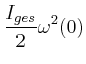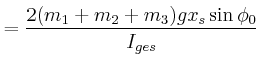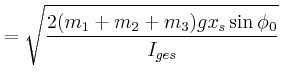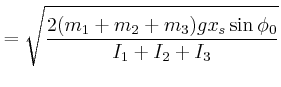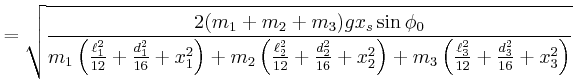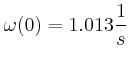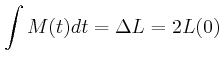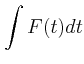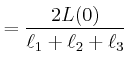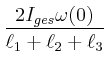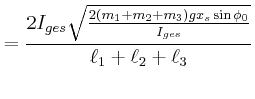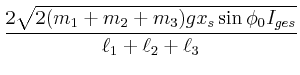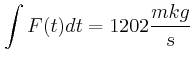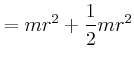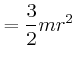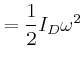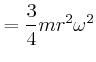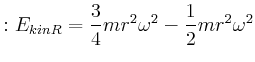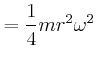![$\displaystyle =\left( \begin{array}[c]{c} a\ 0\ c \end{array} \right)$](img3.gif) |
![$\displaystyle \left( \begin{array}[c]{c} -a\ 0\ -c \end{array} \right)$](img5.gif) |
Die Winkelgeschwindigkeit sei | ![$\displaystyle =\left( \begin{array}[c]{c} 0\ 0\ \omega_{z} \end{array} \right)$](img7.gif) |
Berechnen Sie a)
![]() , b)
, b) ![]() und c)
und c)
![]() .
.
![\includegraphics[width=0.3\textwidth]{ue12-2008-01}](img12.gif)
Der Abstand zwischen ![]() und
und ![]() sei
sei
![]() . Der Durchmesser von
. Der Durchmesser von ![]() sei
sei
![]() , der von
, der von
![]() sei
sei
![]() . Die Atomkerne werden als homogene Kugel angenommen, wobei die Masse von
einem Proton oder einem Neutron etwa
. Die Atomkerne werden als homogene Kugel angenommen, wobei die Masse von
einem Proton oder einem Neutron etwa
![]() ist.
ist.
Berechnen Sie
- das Trägheitsmoment für eine Drehachse durch den Schwerpunkt
(Symmetrie) senkrecht zur Molekülachse,
- das Trägheitsmoment für eine Drehachse parallel zur
Molekülachse durch
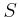 .
.
- Jede dieser Rotationsbewegungen habe eine Energie von
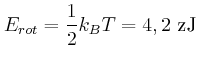
Wie gross ist für die beiden möglichen Rotationsrichtungen
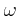 ?
?
Bemerkung: Diese klassische Überlegung kann höchstens ein Anhaltspunkt, aber keine physikalisch korrekte Beschreibung bieten.
![\includegraphics[width=0.25\textwidth]{radarantenne}](img26.gif)
- Berechnen Sie das Trägheitsmoment der Kugel bezüglich der Drehachse.
- Berechnen Sie das Trägheitsmoment der gesamten Anordnung.
- Zur Zeit
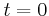 sei die ganze Anordnung in Ruhe. Für
sei die ganze Anordnung in Ruhe. Für 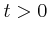 wirke ein konstantes Drehmoment
wirke ein konstantes Drehmoment 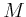 ,
das die Radarantenne in Drehung versetzt. Geben Sie die Winkelgeschwindigkeit
,
das die Radarantenne in Drehung versetzt. Geben Sie die Winkelgeschwindigkeit
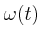 und den zurückgelegten Winkel
und den zurückgelegten Winkel 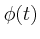 als Funktion der Zeit an.
als Funktion der Zeit an.
- Wo entlang der Verbindungsstange
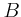 müsste die Drehachse befestigt werden, damit das
Trägheitsmoment minimal wäre?
müsste die Drehachse befestigt werden, damit das
Trägheitsmoment minimal wäre?
- Beschreiben Sie die Bewegung mathematisch.
- Wie gross ist die Winkelbeschleunigung am Anfang?
- Wie gross ist die Winkelgeschwindigkeit, wenn der Schlagbaum die Horizontale erreicht?
- Wie gross ist der Kraftstoss auf das Gegenlager?
- Berechnen Sie mit dem Satz von Steiner das Trägheitsmoment für Drehungen um die momentane Drehachse.
- Berechnen Sie für die Drehung um die momentane Drehachse die gesamte kinetische Energie.
- Wir betrachten das Problem von der Achse des Rades aus. Berechnen Sie hier die gesamte kinetische Energie mit allen Translations- und Rotationskomponenten.
- Der Drehimpuls und die Rotationsenergie sind gleich.
- Der Drehimpuls hat zugenommen, die Rotationsenergie ist gleich.
- Der Drehimpuls hat abgenommen, die Rotationsenergie ist gleich.
- Der Drehimpuls bleibt gleich, die Rotationsenergie hat zugenommen.
- Der Drehimpuls bleibt gleich, die Rotationsenergie hat abgenommen.
- Der Drehimpuls hat zugenommen, die Rotationsenergie hat zugenommen.
- Der Drehimpuls hat zugenommen, die Rotationsenergie hat abgenommen.
- Der Drehimpuls hat abgenommen, die Rotationsenergie hat zugenommen.
- Der Drehimpuls hat abgenommen, die Rotationsenergie hat abgenommen.
![$\displaystyle =m \left[\left( \begin{array}[c]{c} a\\ 0\\ c \end{array} \right)...
...\times\left( \begin{array}[c]{c} -a\\ 0\\ -c \end{array} \right)\right\}\right]$](img55.gif)
![$\displaystyle =m \left[\left( \begin{array}[c]{c} a\\ 0\\ c \end{array} \right)...
...imes\left( \begin{array}[c]{c} 0\\ -a \omega_{z}\\ 0 \end{array} \right)\right]$](img56.gif)
![$\displaystyle =m \left[\left( \begin{array}[c]{c} - a c \omega_{z}\\ 0\\ a^2 \o...
...t( \begin{array}[c]{c} -a c \omega_{z}\\ 0\\ a^2 \omega_{z} \end{array} \right)$](img57.gif)
![$\displaystyle E_{kin} = \frac{1}{2}\left(
\begin{array}[c]{c}
0\\
0\\
\omeg...
...a c \omega_{z}\\
0\\
a^2 \omega_{z}
\end{array}\right)=m a^2 \omega_{z}^{2}$](img59.gif)
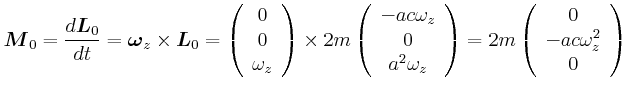
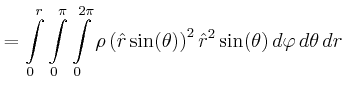
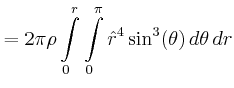
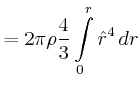
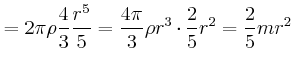
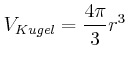
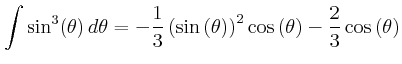
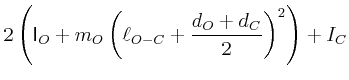
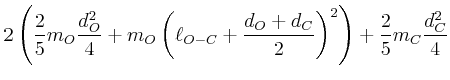
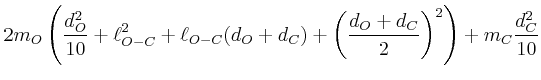
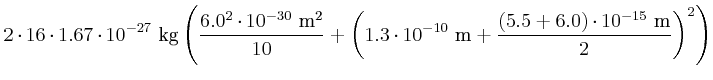
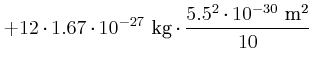
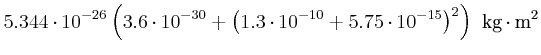
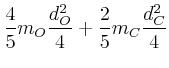
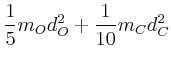
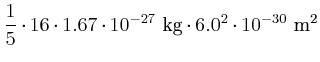
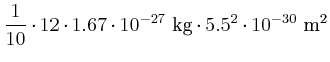
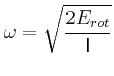
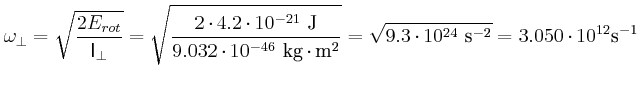
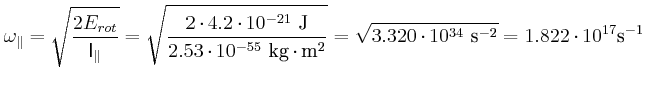
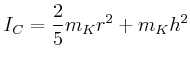
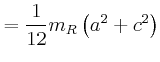
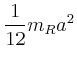
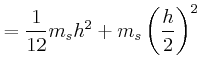
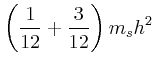
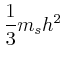
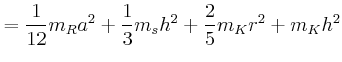
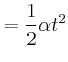
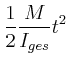
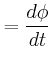
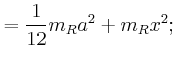
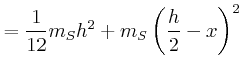
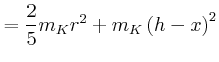
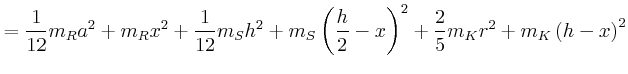
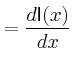
![$\displaystyle =\frac{d}{dx}\left[\frac{1}{12}m_{R} a^2 + m_{R} x^2 +\frac{1}{12...
...eft(\frac{h}{2}-x\right)^2+\frac{2}{5}m_{K}r^2+ m_{K} \left(h-x\right)^2\right]$](img142.gif)
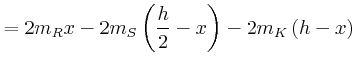
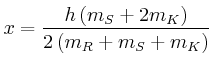
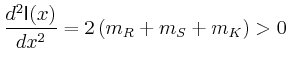
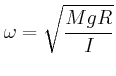
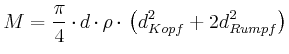
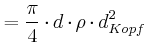
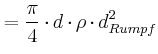
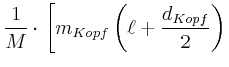
![$\displaystyle +\left.m_{Rumpf}\left( \ell+d_{Kopf}+\frac{d_{Rumpf}}{2}\right) +m_{Rumpf}\left( \ell+d_{Kopf}+\frac{3}{2}d_{Rumpf}\right) \right]$](img160.gif)
![$\displaystyle \mathsf{I}=\left[
\begin{array}[c]{c} \frac{1}{2}m_{Kopf}\left( \...
...Rumpf}\left( \ell+d_{Kopf}+\frac{3}{2}d_{Rumpf}\right) ^{2}
\end{array}\right]
$](img161.gif)