![$\textstyle \parbox{5.7134cm}{\begin{center}\includegraphics[
height=3.0247cm,
width=5.7134cm
]%%
{2003-11-03.eps}%%
\\
RC-Schaltung als Beispiel
\end{center}}$](img1.gif)
Als Beispiel zur z-Transformation betrachten wir eine
RC-Schaltung, die mit einer Einheitsstufenfunktion angesteuert wird.
![$\textstyle \parbox{5.7134cm}{\begin{center}\includegraphics[
height=3.0247cm,
width=5.7134cm
]%%
{2003-11-03.eps}%%
\\
RC-Schaltung als Beispiel
\end{center}}$](img1.gif)
Gleichungen:
| (1) |
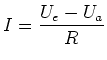 |
(2) |
Also erhalten wir
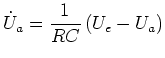 |
(3) |
| Folge: |
(4) | |
| Folge: |
||
Folge: 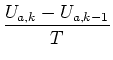 |
Also haben wir
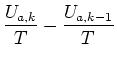 |
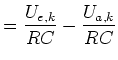 |
(5) |
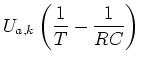 |
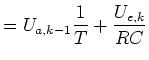 |
(6) |
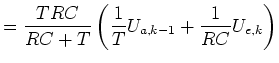 |
(7) | |
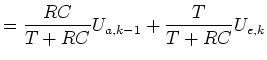 |
||
mit
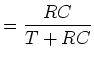 |
||
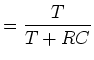 |
Hier können wir die Differenzengleichung lösen
Wir setzen ![]() und erhalten
und erhalten
![]() und
und
![]() . Also ist
. Also ist
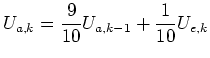 |
(8) |
Das Eingangssignal sei die Folge
| (9) |
und
![]() . Weiter sei
. Weiter sei ![]() Wir vergleichen die Lösung
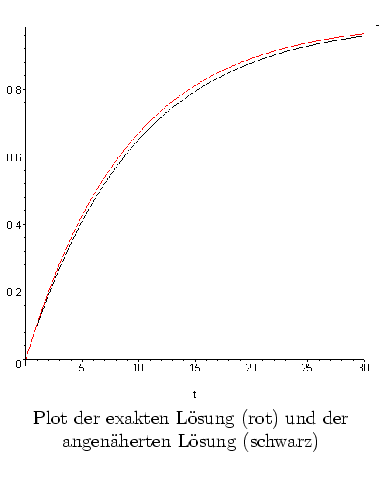
mit der exakten Lösung
Wir vergleichen die Lösung
mit der exakten Lösung
![]() .
(Tabellen im Anhang)
.
(Tabellen im Anhang)
Wir berechnen nun das Resultat mit der z-Transformation und definieren die Namen.
![\begin{displaymath}\begin{array}[c]{ccc} Z\left( U_{a,k}\right) & = & U_{a}^{\as...
...t( U_{e,k}\right) & = & U_{e}^{\ast}\left( z\right) \end{array}\end{displaymath}](img33.gif) |
(10) |
wobei für das mittlere Resultat der Verschiebungssatz verwendet wurde.
Also haben wir
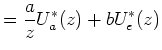 |
(11) | |
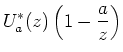 |
||
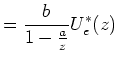 |
||
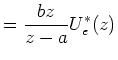 |
Die Eingangsfunktion besteht formal aus einer Reihe von ![]() Eingangspulsen. Die Laplace-Trafo eines verschobenen
Eingangspulsen. Die Laplace-Trafo eines verschobenen ![]() Pulses ist
Pulses ist
![]() . Wir setzen
. Wir setzen ![]() .
.
Also ist die Eingangsfunktion
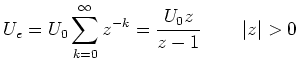 |
(12) |
Wir bekommen
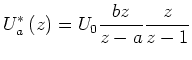 |
(13) |
und nun
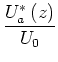 |
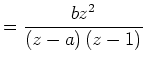 |
(14) |
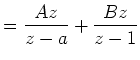 |
||
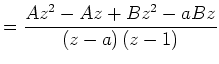 |
Die Partialbruchzerlegung ergibt
| (15) | ||
daraus folgt
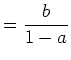 |
(16) | |
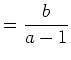 |
Wir lösen die Gleichung
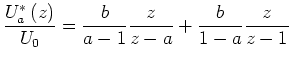 |
(17) |
![\begin{displaymath}\begin{array}[c]{ccc} \frac{z}{z-a} & & a^{k} \frac{z}{z-1} & & \left\{ 1,1,1,\ldots\right\} \end{array}\end{displaymath}](img58.gif) |
(18) |
Also ist
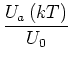 |
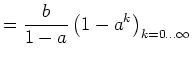 |
(19) |
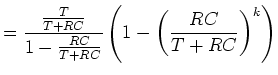 |
||
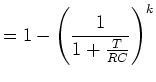 |
Mit unseren Testwerten bekommen wir
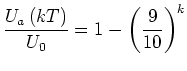 |
(20) |