

Up: Physik 1 für Ingenieure
Übungsblatt 1
Physik für Ingenieure 1
Othmar Marti, (othmar.marti@physik.uni-ulm.de)
16. 10. 2001
Einleitung, Kinematik,
PDF-Datei
- Gegeben seien die Vektoren
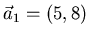 ,
,
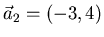 ,
,
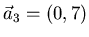 ,
,
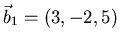 ,
,
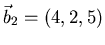 und
und
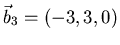 . Berechnen und
konstruieren (mit Massstab und Bleistift) Sie
. Berechnen und
konstruieren (mit Massstab und Bleistift) Sie
-
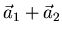 ,
,
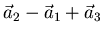
- Suchen sie
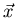 , so dass
, so dass
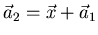
Berechnen Sie
-
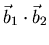 ,
,
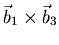 , Winkel zwischen
, Winkel zwischen 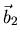 und
und 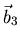
- Welcher kleinster ganzzahliger Vektor
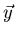 steht senkrecht auf
steht senkrecht auf 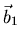 und
und 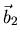 ?
?
- Wie gross ist der Druck in der Tiefe
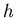 ? Überlegen Sie, welche Grössen relevant sein könnten.
Leiten Sie mit Hilfe der
Einheiten eine Formel her. Stimmt diese Formel nach Ihren Erinnerungen an Ihre Gymnasialzeit?
? Überlegen Sie, welche Grössen relevant sein könnten.
Leiten Sie mit Hilfe der
Einheiten eine Formel her. Stimmt diese Formel nach Ihren Erinnerungen an Ihre Gymnasialzeit?
- Leiten sie ein Gesetz her, das den Druckabfall
![$[\delta p]=\frac{N}{m^2}$](img18.gif) als Funktion der Viskosität
als Funktion der Viskosität
![$[\eta] = Pa \cdot s$](img19.gif) , des in der Zeiteinheit durchfliessenden Volumens
, des in der Zeiteinheit durchfliessenden Volumens
![$[\dot V] = \frac{m^3}{s}$](img20.gif) der Rohrlänge
der Rohrlänge
![$[\ell] = m$](img21.gif) und des Rohrdurchmessers
und des Rohrdurchmessers ![$[d] = m$](img22.gif) . Der Druckabfall ist (warum?) proportional zur Länge
. Der Druckabfall ist (warum?) proportional zur Länge 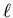 .
.
- Die Gleichung aus der vorherigen Aufgabe 3 soll verifiziert werden. Verwenden sie das Gauss'sche
Fehlerfortpflanzungsgesetz um den Fehler von
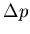 zu berechnen.
zu berechnen.
- Rechnen Sie das Fehlerfortpflanzungsgesetz für relative Fehler aus.
- Die relativen Messfehler sind:
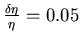 ,
,
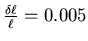 ,
,
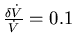 und
und
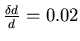 .
.
- Berechnen Sie die konstante Beschleunigung
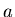 und den zurückgelegten Weg, wenn ein Auto in
und den zurückgelegten Weg, wenn ein Auto in 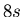 von 0 auf
von 0 auf 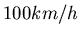 beschleunigt. Was ist die konstante Beschleunigung, wenn auf einer Länge von
beschleunigt. Was ist die konstante Beschleunigung, wenn auf einer Länge von 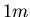 von
von 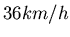 auf 0 beschleunigt wird?
auf 0 beschleunigt wird?
- Ein Zug fahre in einem Bahnhof mit einer konstanten Beschleunigung von
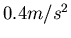 an. Eine Reisende
erreiche einen bestimmten Punkt des Bahnsteiges 6s, nachdem das Ende des Zuges diesen Punkt verliess.
Mit welcher Geschwindigkeit muss sie mindestens laufen, um den Zug noch zu erreichen? Lösen Sie die Gleichung
und skizzieren Sie die Bewegung des Zuges und der Reisenden als Funktion der Zeit (Aufgabe 25, Seite 41,
Tipler, Physik).
an. Eine Reisende
erreiche einen bestimmten Punkt des Bahnsteiges 6s, nachdem das Ende des Zuges diesen Punkt verliess.
Mit welcher Geschwindigkeit muss sie mindestens laufen, um den Zug noch zu erreichen? Lösen Sie die Gleichung
und skizzieren Sie die Bewegung des Zuges und der Reisenden als Funktion der Zeit (Aufgabe 25, Seite 41,
Tipler, Physik).
- Freiwillig: Lösen Sie die Aufgaben 24 und 29 (und weitere), Tipler Seite 41.
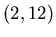 ,
, 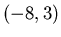
![\includegraphics[width=0.5\textwidth]{Ue1-2.eps}](img37.gif)
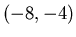
![\includegraphics[width=0.3\textwidth]{Ue1-3.eps}](img39.gif)
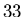 ,
, 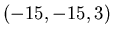 ,
, 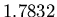
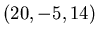
-
![$[p] = kg s^{-2} m^{-1}$](img44.gif) ,
,
![$[\rho] = kg m^{-3}$](img45.gif) ,
,
![$[g] = m s^{-2}$](img46.gif) . Es ist
. Es ist
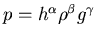 also ist auch
also ist auch
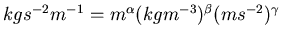 . Der Exponentenvergleich liefert
. Der Exponentenvergleich liefert
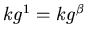 ,
,
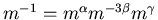 und
und
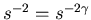 . Aus der dritten
Relation folgt
. Aus der dritten
Relation folgt 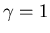 , aus der ersten
, aus der ersten 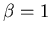 und also
und also
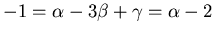 oder
oder
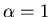 . Also ist (bis auf Vorfaktoren)
. Also ist (bis auf Vorfaktoren) 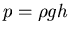 .
.
- Setze
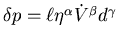 . Daraufhin wird die Einheitengleichung aufgestellt.
Die Einheitengleichung wird nach
. Daraufhin wird die Einheitengleichung aufgestellt.
Die Einheitengleichung wird nach 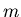 ,
, 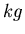 und
und 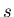 aufgelöst. Man erhält
aufgelöst. Man erhält
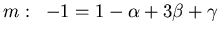
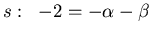
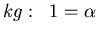
Mit der letzten Gleichung wird die Gleichung ''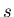 '':
'': 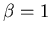 . Daraus wird
. Daraus wird 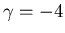 . Das Resultat ist
. Das Resultat ist
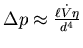 , bis auf einen Vorfaktor die korrekte Gleichung von
Hagen-Poiseuille.
, bis auf einen Vorfaktor die korrekte Gleichung von
Hagen-Poiseuille.
-
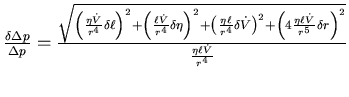
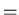
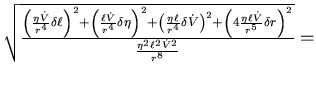
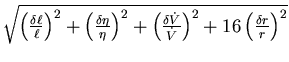
-
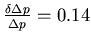 . (auf zwei Stellen)
. (auf zwei Stellen)
-
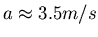 ,
,
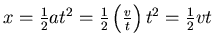 ,
also ist
,
also ist
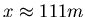 . Beim Bremsen (negative Beschleunigung) ist mit
. Beim Bremsen (negative Beschleunigung) ist mit 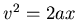
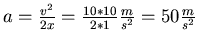 . Zeit:
. Zeit:
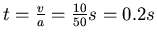 .
.
- Gleichung:
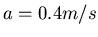 ,
, 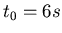 . Es ist
. Es ist
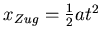 ,
,
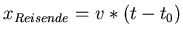 .
Es muss eine Zeit geben, für die
.
Es muss eine Zeit geben, für die
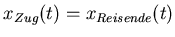 . Damit ist
. Damit ist
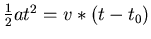 oder
oder
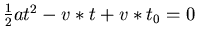
Lösung
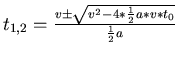 . Es gibt nur eine Lösung,
wenn
. Es gibt nur eine Lösung,
wenn
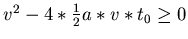 ist. Umgeformt:
ist. Umgeformt:
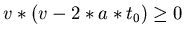 . Also muss
. Also muss
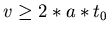 sein. Mit den Zahlen:
sein. Mit den Zahlen:
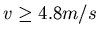 .
.
Zeichnung
![\includegraphics[width=0.7\textwidth]{Ue1-1.eps}](img89.gif)
- Freiwillig: Lösen Sie die Aufgaben 24 und 29 (und weitere), Tipler Seite 41.
Übungsblatt 1
Physik für Ingenieure 1
This document was generated using the
LaTeX2HTML translator Version 99.2beta8 (1.46)
Copyright © 1993, 1994, 1995, 1996,
Nikos Drakos,
Computer Based Learning Unit, University of Leeds.
Copyright © 1997, 1998, 1999,
Ross Moore,
Mathematics Department, Macquarie University, Sydney.
The command line arguments were:
latex2html D:_Ing_111
The translation was initiated by marti on 2001-12-03


Up: Physik 1 für Ingenieure
Othmar Marti
Experimentelle Physik
Universiät Ulm
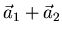 ,
,
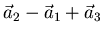
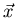 , so dass
, so dass
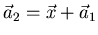
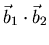 ,
,
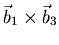 , Winkel zwischen
, Winkel zwischen 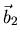 und
und 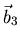
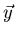 steht senkrecht auf
steht senkrecht auf 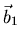 und
und 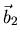 ?
?
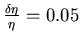 ,
,
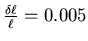 ,
,
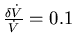 und
und
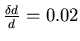 .
.
![\includegraphics[width=0.5\textwidth]{Ue1-2.eps}](img37.gif)
![\includegraphics[width=0.3\textwidth]{Ue1-3.eps}](img39.gif)
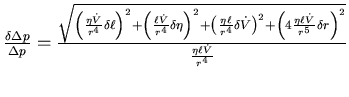
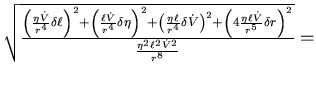
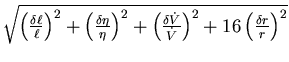
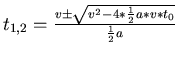 . Es gibt nur eine Lösung,
wenn
. Es gibt nur eine Lösung,
wenn
![\includegraphics[width=0.7\textwidth]{Ue1-1.eps}](img89.gif)