

Up: Physik 1 für Ingenieure
Übungsblatt 10
Physik für Ingenieure 1
Othmar Marti, (othmar.marti@physik.uni-ulm.de)
18. 12. 2001
Spezielle Relativitätstheorie
-
![\includegraphics[width=0.5\textwidth]{aufg1.eps}](img1.gif)
Schliesse
einen 6 m langen Stab in einer 3 m tiefen Garage ein (Fig. 8.9). Dabei verstehen wir
unter Einschliessen des Stabes: Das Stabende E soll unbeschadet das Garagetor passieren.
Die Längenangaben in der Abbildung beziehen sich auf die Längen in den Ruhesystemen der
jeweiligen Objekte.
- Ein Raumschiff verlasse die Erde in Richtung
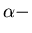 Centauri, der 4 Lichtjahre
entfernt ist. Die Geschwindigkeit des Raumschiffs betrage
Centauri, der 4 Lichtjahre
entfernt ist. Die Geschwindigkeit des Raumschiffs betrage 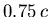 . Wie lange braucht
es für diese Entfernung im Ruhesystem der Erde und im Ruhesystem eines Astronauten.
. Wie lange braucht
es für diese Entfernung im Ruhesystem der Erde und im Ruhesystem eines Astronauten.
- Zwei Ereignisse auf der y-Achse finden in einem Inertialsystem
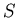 im Abstand
im Abstand
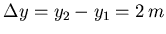 und mit einer Zeitdifferenz
und mit einer Zeitdifferenz
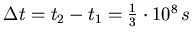 statt.
statt.
- Bestimme die minimale Geschwindigkeit
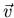 (Richtung und Betrag), die ein
Inertialsystem
(Richtung und Betrag), die ein
Inertialsystem  haben muss, damit die beiden Ereignisse in
haben muss, damit die beiden Ereignisse in 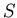 gleichzeitig sind.
gleichzeitig sind.
- Wie gross darf die Zeitdifferenz
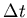 maximal sein, damit in einem in
maximal sein, damit in einem in 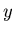 -Richtung
bewegten Inertialsystem
-Richtung
bewegten Inertialsystem 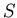 die beiden Ereignisse gleichzeitig sind?
die beiden Ereignisse gleichzeitig sind?
- Der Weihnachtsmann besucht einen Viertel aller Familien in der Weihnachtsnacht.
Dabei kreist er mit unverminderter Geschwindigkeit während
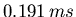 über jeder
Familie.
über jeder
Familie.
- Wie lange ist, von Süden gesehen, die Kufe des Schlittens, wenn der
Weihnachtsmann von Westen nach Osten fliegt?
- Wie lange arbeitet der Weihnachtsmann?
- Welche Farbe hat sein Gewand, wenn er auf einen zukommt?
- Welche Farbe hat sein Gewand, wenn er sich wegbewegt?
- Würden Sie zustimmen, dass noch niemand den Weihnachtsmann gesehen hat,
weil er, von vorne betrachtet, wie ein Jäger aussieht und weil er, von hinten
betrachtet nicht sichtbar ist?
Benutzen Sie die folgenden Zahlen:
- Der Erdradius ist
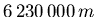 .
.
- Die Erde ist mit
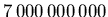 Einwohnern besiedelt.
Einwohnern besiedelt.
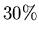 der Erdoberfläche ist besiedelt.
der Erdoberfläche ist besiedelt.
- Jede Familie hat 4 Mitglieder.
- Alle Familien wohnen gleichabständig auf einem Quadratgitter
- Der Weihnachtsmann fährt mit seinem Schlitten entlang einer Mäanderbahn
(Wie im Fernsehapparat).
- Der Schlitten des Weihnachtsmannes hat Kufen von 10 m Länge.
- Das Gewand des Weihnachtsmannes ist leuchtend rot, dies entspricht
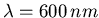 Wellenlänge.
Wellenlänge.
- Der Weihnachtsmann arbeitet 24 h.
- Ruhesystem der Garage: Es muss
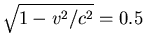 sein, also
sein, also
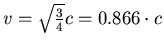 .
.
- Sobald das hintere Ende die Garagentür passiert hat, wird diese geschlossen.
- Darauf wird der Stab von der Hinterseite der Garage gebremst, der Stab nimmt nun
im Ruhesystem der Garage seine ursprüngliche Länge an. Es ist nicht klar, ob die
Garage, ihre Rückwand, das Tor oder der Stab einzeln oder alle zusammen kaputt gehen.
- Wir betrachten das Problem aus der Sicht des Stabes.
- Die Garage rast mit
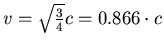 auf den Stab zu
und ist deshalb noch
auf den Stab zu
und ist deshalb noch 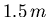 lang!
lang!
- Die Zeit
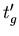 , diue die Garagentüre braucht, um das Stabende
, diue die Garagentüre braucht, um das Stabende 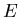 zu erreichen,
nachdem der Stabanfang
zu erreichen,
nachdem der Stabanfang 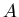 die Garagenrückwand berührt hat, ist
die Garagenrückwand berührt hat, ist
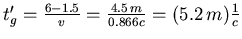
- Die Zeit
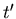 wird benötigt, um die vom Aufprall von
wird benötigt, um die vom Aufprall von  herrührende Störung nach
herrührende Störung nach
 zu übermitteln ist
zu übermitteln ist
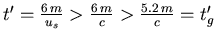 , da
, da 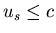 sein muss.
sein muss.
- Das Stabende ist an der Garagentüre vorbei, bevor es vom Unglück des Anfangs
erfahren kann.
- Im Ruhesystem der Erde ist
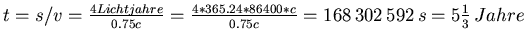
- Im Raumschiff vergeht die Zeit
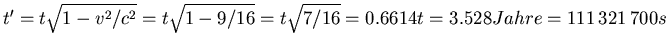
- Alternativ sagt man, die Distanz zu
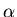 -Centauri ist
-Centauri ist
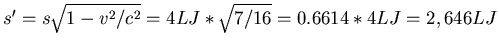 . Die Flugzeit ist
. Die Flugzeit ist
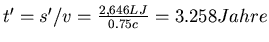 , konsistent mit der obigen Überlegung.
, konsistent mit der obigen Überlegung.
-
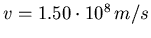 in die y-Richtung
in die y-Richtung
- Die obige Abbuldung zeigt die Lage der beiden Ereignisse.
- Die Zeitdilatation oder die Längenkontraktion ist dann maximal, wenn die
Geschwindigkeit in Richtung der y-Achse liegt.
- Wenn die beiden Ereignisse gleichzeitig sein sollen, muss B's jetzt, seine
'r'-Achse durch die beiden Ereignisse gehen.
- Der Winkel
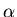 gibt die Geschwindigkeit an:
gibt die Geschwindigkeit an:
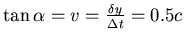 .
.
-
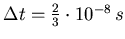
- Wenn die Steigung von B's jetzt, seiner 'r'-Achse
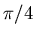 ist, wenn er sich also
mit
ist, wenn er sich also
mit 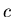 fortbewegt, ist dadurch die maximal mögliche Zeitdifferenz gegeben.
fortbewegt, ist dadurch die maximal mögliche Zeitdifferenz gegeben.
- Also muss
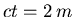 sein.
sein.
- Damit folgt das obige Resultat.
- Erdoberfläche
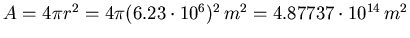
- Besiedelte Oberfläche:
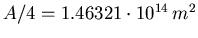
- Anzahl Familien
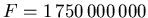
- Fläche pro Familie
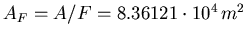
- Abstand zwischen zwei Familien
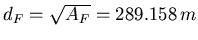
- Flugweg zwischen den Familien
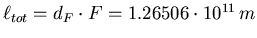
- Entladezeit pro Familie
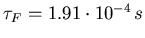
- Totale Entladezeit
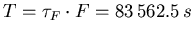
- 24 Stunden sind
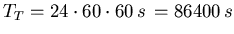
- Die Flugzeit ist
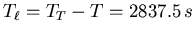
- Die Geschwindigkeit des Weihnachtsmannes ist
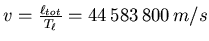
- oder
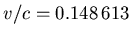
- Es ist
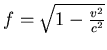
- Die sichtbare Länge ist
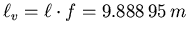
- Die Zeit läuft langsamer ab, also wird nur
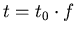 gearbeitet,
gearbeitet,
- Arbeitszeit
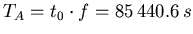
- Dopplereffekt:
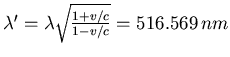 . Dies ist die grüne Farbe.
. Dies ist die grüne Farbe.
- Dopplereffekt:
 . Dies ist eine infrarote Farbe, also nicht mehr sichtbar.
. Dies ist eine infrarote Farbe, also nicht mehr sichtbar.
- Haben Sie eine bessere Erklärung?
Gibt es den
Weihnachtsmann?
Keine bekannte
Spezies der Gattung Rentier kann fliegen. ABER es gibt 300.000 Spezies von
lebenden Organismen, die noch klassifiziert werden müssen, und obwohl es sich dabei
hauptsächlich um Insekten und Bakterien handelt, schließt dies nicht mit letzter
Sicherheit fliegende Rentiere aus, die nur der Weihnachtsmann bisher gesehen hat.
Es gibt 2 Milliarden Kinder (Menschen unter 18) auf der Welt. ABER da der Weihnachtsmann (scheinbar) keine Moslems, Hindu, Juden und Buddhisten beliefert, reduziert sich seine Arbeit auf etwa 15Der Weihnachtsmann hat einen 31-Stunden-Weihnachtstag, bedingt durch die verschiedenen
Zeitzonen, wenn er von Osten nach Westen reist (was logisch erscheint). Damit ergeben
sich 822,6 Besuche pro Sekunde. Somit hat der Weihnachtsmann für jeden christlichen
Haushalt mit braven Kindern rund 1 Millisekunde Zeit für seine Arbeit: Parken, aus dem
Schlitten springen, den Schornstein runterklettern, die Socken füllen, die übrigen
Geschenke unter dem Weihnachtsbaum verteilen, alle übriggebliebenen Reste des
Weihnachtsessens vertilgen, den Schornstein wieder raufklettern und zum nächsten Haus
fliegen. Angenommen, daß jeder dieser 91,8 Millionen Stops gleichmäßig auf die ganze Erde
verteilt sind (was natürlich, wie wir wissen, nicht stimmt, aber als Berechnungsgrundlage
akzeptieren wir dies), erhalten wir nunmehr 1,3 km Entfernung von Haushalt zu Haushalt,
eine Gesamtentfernung von 120,8 Millionen km, nicht mitgerechnet die Unterbrechungen für
das, was jeder von uns mindestens einmal in 31 Stunden tun muß, plus Essen usw. Das
bedeutet, daß der Schlitten des Weihnachtsmannes mit 1040 km pro Sekunde fliegt, also der
3.000-fachen Schallgeschwindigkeit. Zum Vergleich: das schnellste von Menschen gebaute
Fahrzeug, der Ulysses Space Probe, fährt mit lächerlichen 43,8 km pro Sekunde. Ein
gewöhnliches Rentier schafft höchstens 24 km pro Stunde.
Die Ladung des Schlittens führt zu einem weiteren interessanten Effekt. Angenommen, jedes
Kind bekommt nicht mehr als ein mittelgroßes Lego-Set (etwa 1 kg), dann hat der Schlitten
ein Gewicht von 378.000 Tonnen geladen, nicht gerechnet den Weihnachtsmann, der
übereinstimmend als übergewichtig beschrieben wird. Ein gewöhnliches Rentier kann nicht
mehr als 175 kg ziehen. Selbst bei der Annahme, daß ein fliegendes Rentier das
10-fache normale Gewicht ziehen kann, braucht man für den Schlitten nicht acht oder
vielleicht neun Rentiere. Man braucht 216.000 Rentiere. Das erhöht das Gewicht - den
Schlitten selbst noch nicht einmal eingerechnet - auf 410.400 Tonnen. Nochmals zum
Vergleich: das ist mehr als das vierfache Gewicht der Queen Elizabeth.
410.400 Tonnen bei einer Geschwindigkeit von 1040 km/s erzeugt einen ungeheuren
Luftwiderstand - dadurch werden die Rentiere aufgeheizt, genauso wie ein Raumschiff, das
wieder in die Erdatmosphäre eintritt. Das vorderste Paar Rentiere muß dadurch pro Sekunde
16,6 Trillionen Joule Energie absorbieren. Jedes. Anders ausgedrückt: sie werden
praktisch augenblicklich in Flammen aufgehen, das nächste Paar Rentiere wird dem
Luftwiderstand preisgegeben, und es wird ein ohrenbetäubender Knall erzeugt. Das gesamte
Team von Rentieren wird innerhalb von 5 Millisekunden vaporisiert. Der Weihnachtsmann
wird währenddessen einer Beschleunigung von der Größe der 17.500-fachen Erdbeschleunigung
ausgesetzt. Ein 120 kg schwerer Weihnachtsmann (was der Beschreibung nach lächerlich
wenig sein muß) würde an das Ende seines Schlittens genagelt - mit einer Kraft von 20,6
Meganewton. Damit kommen wir zu dem Schluß: Wenn der Weihnachtsmann irgendwann einmal die
Geschenke gebracht hat, ist er heute tot.
Übungsblatt 10
Physik für Ingenieure 1
This document was generated using the
LaTeX2HTML translator Version 99.2beta8 (1.46)
Copyright © 1993, 1994, 1995, 1996,
Nikos Drakos,
Computer Based Learning Unit, University of Leeds.
Copyright © 1997, 1998, 1999,
Ross Moore,
Mathematics Department, Macquarie University, Sydney.
The command line arguments were:
latex2html D:_Ing_11010
The translation was initiated by marti on 2002-01-08


Up: Physik 1 für Ingenieure
Othmar Marti
Experimentelle Physik
Universiät Ulm
![\includegraphics[width=0.5\textwidth]{aufg1.eps}](img1.gif)
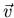 (Richtung und Betrag), die ein
Inertialsystem
(Richtung und Betrag), die ein
Inertialsystem  haben muss, damit die beiden Ereignisse in
haben muss, damit die beiden Ereignisse in  gleichzeitig sind.
gleichzeitig sind.
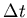 maximal sein, damit in einem in
maximal sein, damit in einem in 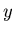 -Richtung
bewegten Inertialsystem
-Richtung
bewegten Inertialsystem 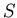 die beiden Ereignisse gleichzeitig sind?
die beiden Ereignisse gleichzeitig sind?
![\includegraphics[width=0.35\textwidth]{weihnachtsmann3.eps}](img11.gif)
![\includegraphics[width=0.2\textwidth]{weihnachtsmann.eps}](img12.gif)
![\includegraphics[width=0.35\textwidth]{wmann.eps}](img13.gif)
![\includegraphics[width=0.5\textwidth]{aufg3.eps}](img35.gif)
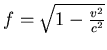
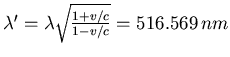 . Dies ist die grüne Farbe.
. Dies ist die grüne Farbe.
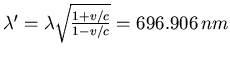 . Dies ist eine infrarote Farbe, also nicht mehr sichtbar.
. Dies ist eine infrarote Farbe, also nicht mehr sichtbar.