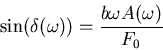

Up: Physik 1 für Ingenieure
Übungsblatt 13
Physik für Ingenieure 1
Othmar Marti, (othmar.marti@physik.uni-ulm.de)
22. 1. 2002
Schwingungen
Zuerst nachdenken, dann in Ihrer Vorlesungsmitschrift nachschauen und erst dann
wild lostrechnen!
-
Ein kleines Teilchen der Masse
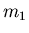 gleite reibungsfrei in einer kugelförmigen
Schale mit dem Radius
gleite reibungsfrei in einer kugelförmigen
Schale mit dem Radius 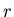 .
.
- Zeigen Sie, dass die Bewegung die gleiche wäre, wenn das Teilchen an einem
Faden der Länge
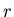 aufgehängt wäre.
aufgehängt wäre.
- Die Abbildung zeigt ein Teilchen, das nur ein wenig (
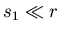 ) vom
tiefsten Punkt ausgelenkt ist. Ein zweites Teilchen der Masse
) vom
tiefsten Punkt ausgelenkt ist. Ein zweites Teilchen der Masse 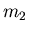 ist an der
anderen Seite um
ist an der
anderen Seite um
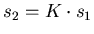 (
(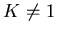 ,
, 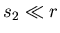 ) ausgelenkt. Wo treffen
sich die Teilchen, wenn sie gleichzeitig losgelassen werden? Warum?
) ausgelenkt. Wo treffen
sich die Teilchen, wenn sie gleichzeitig losgelassen werden? Warum?
- Wo treffen sich die Teilchen, wenn sie gleichzeitig losgelassen werden,
aber nun perfekt rollen und nicht gleiten?
- Ein Kind auf einer Schaukel schwinge mit einer Periode von
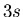 .
Zusammen mit der Schaukel habe es ein Gewicht von
.
Zusammen mit der Schaukel habe es ein Gewicht von 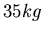 . Das Kind werde von einem
geduldigen Vater so angeschaukelt, dass die Amplitude konstant bleibt. Am tiefsten
Punkt betrage die Geschwindigkeit des Kindes
. Das Kind werde von einem
geduldigen Vater so angeschaukelt, dass die Amplitude konstant bleibt. Am tiefsten
Punkt betrage die Geschwindigkeit des Kindes 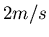 .
.
- Wie gross ist die Gesamtenergie von Schaukel und Kind?
- Wie gross wäre die Periodendauer, wenn der Vater
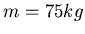 anstelle des
Kindes auf der Schaukel sässe?
anstelle des
Kindes auf der Schaukel sässe?
- Wieviel Energie geht der Schaukel pro Periode verloren, wenn der Q-Faktor
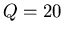 ist?
ist?
- Wieviel Leistung muss der Vater beisteuern?
Beachten Sie: Eine Schaukel wird gewöhnlich nicht sinusförmig angestossen.
Jedoch muss bei konstanter Amplitude der Energieverlust der Schaukel durch eine
äussere Quelle ersetzt werden muss. Diese Energie kann durch die Schaukelbewegungen
des Kindes (was an der Schaukel wird verändert?) oder durch jemanden, der anstösst,
aufgebracht werden.
-
Ein physikalisches Pendel bestehe aus einer Kugel mit dem Radius
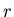 und der Masse
und der Masse
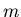 , die an einem Faden aufgehängt sei (siehe Abbildung). Der Abstand vom
Schwerpunkt zum Aufhängungspunkt sei
, die an einem Faden aufgehängt sei (siehe Abbildung). Der Abstand vom
Schwerpunkt zum Aufhängungspunkt sei 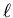 . Wenn
. Wenn 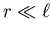 ist, wird dieses
Pendel oft als mathematisches Pendel behandelt.
ist, wird dieses
Pendel oft als mathematisches Pendel behandelt.
- Zeigen sie, dass die Schwingungsdauer für kleine Auslenkungen durch
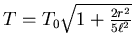 gegeben ist, wobei
gegeben ist, wobei
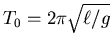 die Schwingungsdauer des mathematischen Pendels der Länge
die Schwingungsdauer des mathematischen Pendels der Länge 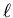 ist.
ist.
- Zeigen Sie, dass für
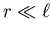 die Schwingungsdauer durch
die Schwingungsdauer durch
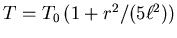 angenähert werden kann.
angenähert werden kann.
- Bestimmen Sie den Fehler in der Schwingungsdauer, der durch diese Näherung
entsteht, für den Fall
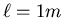 und
und 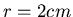 .
.
- Wie gross muss der Radius der Kugel sein, damit der Fehler 1 % beträgt?
- Leiten sie einen Ausdruck für die durch eine antreibende Kraft zugeführte
durchschnittliche Leistung her. (Siehe den Abschnitt ,,Erzwungene (gedämpfte) Schwingung und
Resonanz'' vom 16.1. 2002).
- Zeigen sie, dass die momentan zugeführte Leistung einer treibenden Kraft
durch
gegeben ist.
- Verwenden Sie das Additionstheorem, um sie auf die Form
zu
bringen.
- Zeigen Sie, dass der zeitliche Mittelwert des zweiten Summanden aus
4b verschwindet und deshalb folgt:
.
- Nach Gleichung (8.67) (
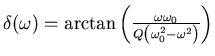 )
für
)
für 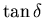 lässt sich ein rechtwinkliges Dreieck konstruieren, bei dem
die dem Winkel
lässt sich ein rechtwinkliges Dreieck konstruieren, bei dem
die dem Winkel 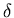 gegenüberliegende Seite
gegenüberliegende Seite 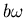 und die anliegende
Seite
und die anliegende
Seite
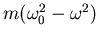 entspricht. zeigen Sie anhand dieses Dreieckes,
dass
entspricht. zeigen Sie anhand dieses Dreieckes,
dass
ist.
- Ersetzen sie
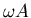 mit Hilfe der Ergebnisse von 4c und 4d und
zeigen sie, dass die durchschnittliche Leistungsaufnahme in der Form
mit Hilfe der Ergebnisse von 4c und 4d und
zeigen sie, dass die durchschnittliche Leistungsaufnahme in der Form
geschrieben werden kann.
- Berechnen Sie Näherungslösungen für
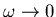 und
und
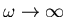 . Welche Leistung wird bei
. Welche Leistung wird bei
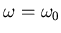 verbraucht.
verbraucht.
- Da der Abstand der Bahn zum Krümmungsmittelpunkt konstant ist, kann man
ohne die Bewegung zu stören vom Krümmungsmittelpunkt zum Teilchen einen Faden spannen.
Wenn die Unterlage entfernt wird, folgt das Teilchen immer noch der gleichen Bahn. Da
keine zusätzlichen Kräfte senkrecht zur Fadenlinie (tangential) ausgeübt werden da die
radialen Zwangskräfte gleich sind, ist die Bewegung gleich.
- Da die Periodendauer bei einem Pendel mit kleiner Auslenkung
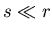 unabhängig von der Auslenkung ist, ist die Zeit die ein Teilchen vom Maximum bis
zu tiefsten Punkt braucht, nämlich
unabhängig von der Auslenkung ist, ist die Zeit die ein Teilchen vom Maximum bis
zu tiefsten Punkt braucht, nämlich 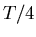 , gleich. Die beiden Teilchen treffen sich
am tiefsten Punkt (wenn man annimmt, dass die Ausdehnung der Teilchen klein gegen
die Auslenkung ist).
, gleich. Die beiden Teilchen treffen sich
am tiefsten Punkt (wenn man annimmt, dass die Ausdehnung der Teilchen klein gegen
die Auslenkung ist).
- Bei der gleitenden Bewegung wird potentielle Energie in kinetische Energie
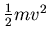 umgewandelt. Wenn eine rollende Bewegung vorhanden ist, wird die
potentielle Energie in Translationsenergie
umgewandelt. Wenn eine rollende Bewegung vorhanden ist, wird die
potentielle Energie in Translationsenergie
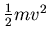 und in
Rotationsenergie
und in
Rotationsenergie
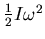 aufgeteilt. Nun ist
aufgeteilt. Nun ist
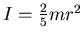 und die Zwangsbedingung ist, dass
und die Zwangsbedingung ist, dass 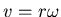 . Also ist die Rotationsenergie
. Also ist die Rotationsenergie
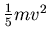 und damit die Gesamtenergie
und damit die Gesamtenergie
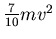 . Die
Periodendauer des Pendels wird grösser, ist aber immer noch unabhängig von der
Auslenkung: die Kugeln treffen sich in der Mitte.
. Die
Periodendauer des Pendels wird grösser, ist aber immer noch unabhängig von der
Auslenkung: die Kugeln treffen sich in der Mitte.
- Am tiefsten Punkt ist die gesamte Energie kinetische Energie. Also ist
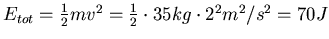
- Die Periodendauer eines Pendels ist unabhängig von der Masse, also ist sie beim
Vater gleich wie beim Kind.
- Die Definition des Q-Faktors ist
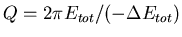 .
.
Also
ist
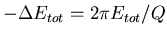 oder
oder
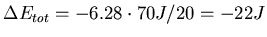
- Die Periodendauer ist
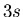 , also ist die Leistung des Vaters
, also ist die Leistung des Vaters
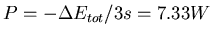 .
.
- Die Schwingungsdauer des physikalischen Pendels ist
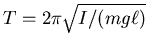 . Das Trägheitsmoment einer Kugel ist
. Das Trägheitsmoment einer Kugel ist
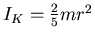 .
Nun dreht sich die Kugel um den Aufhängepunkt. Nach dem Satz von Steiner ist
.
Nun dreht sich die Kugel um den Aufhängepunkt. Nach dem Satz von Steiner ist
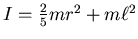 . Die Schwingungsdauer ist dann
. Die Schwingungsdauer ist dann
- Für
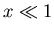 ist
ist
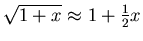 . Die Bedingung in
unserem Falle heisst
. Die Bedingung in
unserem Falle heisst
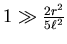 oder
oder
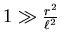 oder
oder 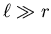 . Dann ist
. Dann ist
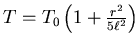 .
.
- Wir setzen ein und erhalten
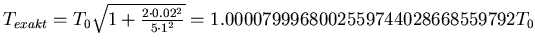
sowie
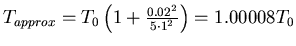 .
.
Der Fehler ist
also
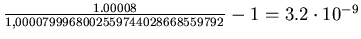 .
.
- Wir setzen
Wir erhalten
Wir setzen
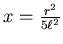
Wir setzen
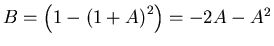 und erhalten
und erhalten
oder 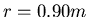
- Die Anregung ist definitionsgemäss
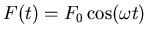 . Die Lösung
der Bewegungsgleichung ist
. Die Lösung
der Bewegungsgleichung ist
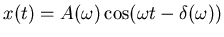 . Dann
ist
. Dann
ist
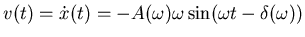 . Die
Leistung ist also
. Die
Leistung ist also
- Es ist
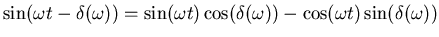 . Wir setzen ein und sortieren nach den
Winkelfunktionen
. Wir setzen ein und sortieren nach den
Winkelfunktionen
- Es ist
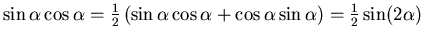 . Der Mittelwert
. Der Mittelwert
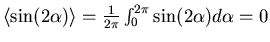 . Da das Mittel über eine Schwingungsperiode
dem Mittel über
. Da das Mittel über eine Schwingungsperiode
dem Mittel über  entspricht, ist auch
entspricht, ist auch
Der Mittelwert von
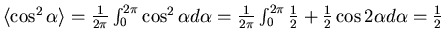 , da der zweite Summand im Integral null ergibt.
Damit ist
, da der zweite Summand im Integral null ergibt.
Damit ist
.
- Wir haben
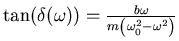 und interpretieren dies im
Sinne der Aufgabenstellung [
und interpretieren dies im
Sinne der Aufgabenstellung [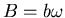 und
und
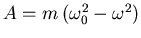 ].
Dann ist die Hypothenuse
].
Dann ist die Hypothenuse
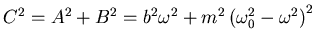 . Nun ist
. Nun ist
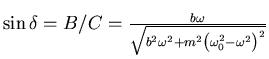
Setzen wir
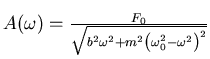 ein, so bekommen wir
ein, so bekommen wir
- Wir setzen
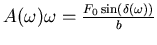 und setzen ein.
und setzen ein.
Die Elimination von
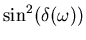 liefert schliesslich
liefert schliesslich
Für kleine Frequenzen ist
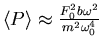 . Für grosse Frequenzen ist
. Für grosse Frequenzen ist
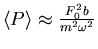 . Für
. Für
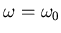 ist
ist
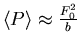 .
.
Übungsblatt 13
Physik für Ingenieure 1
This document was generated using the
LaTeX2HTML translator Version 99.2beta8 (1.46)
Copyright © 1993, 1994, 1995, 1996,
Nikos Drakos,
Computer Based Learning Unit, University of Leeds.
Copyright © 1997, 1998, 1999,
Ross Moore,
Mathematics Department, Macquarie University, Sydney.
The command line arguments were:
latex2html D:_Ing_11313
The translation was initiated by marti on 2002-01-29


Up: Physik 1 für Ingenieure
Othmar Marti
Experimentelle Physik
Universiät Ulm
![\includegraphics[width=0.5\textwidth]{ue13-1.eps}](img1.gif)
 aufgehängt wäre.
aufgehängt wäre.
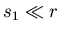 ) vom
tiefsten Punkt ausgelenkt ist. Ein zweites Teilchen der Masse
) vom
tiefsten Punkt ausgelenkt ist. Ein zweites Teilchen der Masse 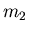 ist an der
anderen Seite um
ist an der
anderen Seite um
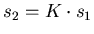 (
(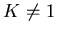 ,
, 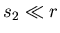 ) ausgelenkt. Wo treffen
sich die Teilchen, wenn sie gleichzeitig losgelassen werden? Warum?
) ausgelenkt. Wo treffen
sich die Teilchen, wenn sie gleichzeitig losgelassen werden? Warum?
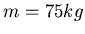 anstelle des
Kindes auf der Schaukel sässe?
anstelle des
Kindes auf der Schaukel sässe?
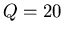 ist?
ist?
![\includegraphics[width=0.4\textwidth]{ue13-3.eps}](img14.gif)
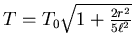 gegeben ist, wobei
gegeben ist, wobei
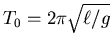 die Schwingungsdauer des mathematischen Pendels der Länge
die Schwingungsdauer des mathematischen Pendels der Länge 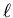 ist.
ist.
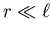 die Schwingungsdauer durch
die Schwingungsdauer durch
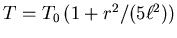 angenähert werden kann.
angenähert werden kann.
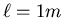 und
und 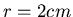 .
.
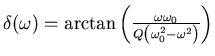 )
für
)
für 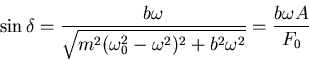
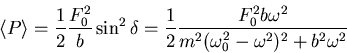
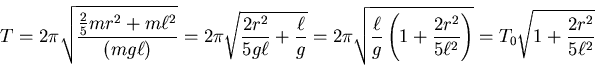
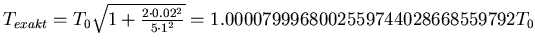
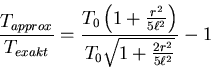
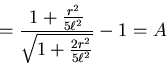
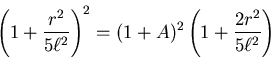
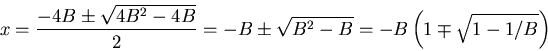
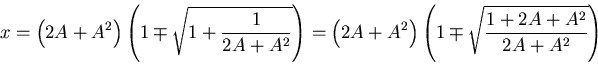
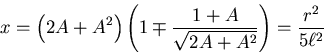
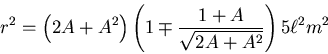
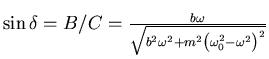
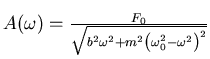 ein, so bekommen wir
ein, so bekommen wir