

Up: Physik 1 für Ingenieure
Übungsblatt 14
Physik für Ingenieure 1
Othmar Marti, (othmar.marti@physik.uni-ulm.de)
29. 1. 2002
Schwingungen
Zuerst nachdenken, dann in Ihrer Vorlesungsmitschrift nachschauen und erst dann
wild losrechnen!
- Mit Hilfe transversaler harmonischer Wellen soll Leistung auf einer Saite übertragen
werden.Die Ausbreitungsgeschwindigkeit der Wellen betrage
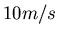 bei einer
Massebelegung des Drahtes von
bei einer
Massebelegung des Drahtes von 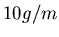 . Die Energiequelle schwinge mit einer
Amplitude von
. Die Energiequelle schwinge mit einer
Amplitude von 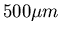 .
.
- Wie gross ist die Durchschnittsleistung, die bei 400 Hz über den Draht
übertragen wird?
- Die Übertragungsleistung kann erhöht werden, wenn die Spannung im Draht, die
Frequenz der Quelle oder die Amplitude der Wellen erhöht wird. Wie müsste sich
jede einzelne dieser Grössen ändern, damit die Übertragungsleistung auf das
100-fache ansteigt.
- Welche dieser Grössen lässt sich am leichtesten ändern?
- Zwei Drähte unterschiedlicher Massenbelegung werden zusammengebunden und mit
einer Kraft
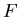 gespannt. Die Ausbreitungsgeschwindigkeit sei im ersten Draht doppelt
so gross wie im zweiten. Eine harmonische Welle, die den ersten Draht entlangwandert,
wird an der Verbindungsstelle der beiden Drähte teilweise reflektiert, teilweise geht
sie auf den zweiten Draht über und wandert dort weiter (Transmission). Die Amplitude
der reflektierten Welle sei halb so gross wie die der transmittierten Welle.
gespannt. Die Ausbreitungsgeschwindigkeit sei im ersten Draht doppelt
so gross wie im zweiten. Eine harmonische Welle, die den ersten Draht entlangwandert,
wird an der Verbindungsstelle der beiden Drähte teilweise reflektiert, teilweise geht
sie auf den zweiten Draht über und wandert dort weiter (Transmission). Die Amplitude
der reflektierten Welle sei halb so gross wie die der transmittierten Welle.
- Wie gross ist der Energieanteil der Wellen, die an der Verbindungsstelle
reflektiert und transmittiert werden (bezogen auf die ursprüngliche Energie?).
- Wie gross sind die Amplituden, wenn die ursprüngliche Welle die Amplitude
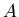 besass.
besass.
- Für die Massenbelegung zweier verbundener Saiten gelte
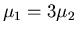 bei
gleicher Saitenspannung. Bei einer Frequenz von
bei
gleicher Saitenspannung. Bei einer Frequenz von 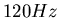 wandern Wellen der
Wellenlänge
wandern Wellen der
Wellenlänge 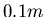 die erste Saite mit der Massenbelegung
die erste Saite mit der Massenbelegung 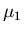 entlang.
entlang.
- Wie gross ist die Ausbreitungsgeschwindigkeit auf der ersten Saite?
- Wie gross ist die Ausbreitungsgeschwindigkeit auf der zweiten Saite?
- Welche Wellenlänge haben die Wellen auf der zweiten Saite?
- Berechnen sie mit einem Ansatz analog zur Vorlesung die Eigenschwingungen von drei
identischen, mit masselosen gleichen Federn gekoppelten Pendeln, die auf einer Linie angeordnet sind.
- Berechnen sie mit einem Ansatz analog zur Vorlesung die Eigenschwingungen von drei
identischen, mit masselosen gleichen Federn gekoppelten Pendeln, die auf einem Kreis angeordnet
sind.
Vernachlässigen Sie für die Rechnung jegliche Effekte der Krümmung. Die Anordnung
''auf dem Kreis'' bedeutet, dass das dritte Pendel mit einer Feder an das erste
gekoppelt ist. Wenn das zweite Pendel rechts vom ersten ist, dann ist das 3. Pendel
rechts vom 2. und, formal, das 1. Pendel rechts vom 3.
- Die Leistung einer Welle ist
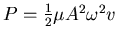 . Eingesetzt
erhalten wir
. Eingesetzt
erhalten wir
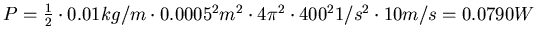
- Die Amplitude müsste 10 mal grösser sein
Die Frequenz müsste 10 mal grösser sein
Die Geschwindigkeit ist
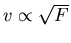 Um die Leistung hundert mal
grösser zu machen, muss die Geschwindigkeit hundert mal und die Spannung
10000 mal höher sein.
Um die Leistung hundert mal
grösser zu machen, muss die Geschwindigkeit hundert mal und die Spannung
10000 mal höher sein.
- Die Erhöhung der Geschwindigkeit ist nicht machbar. Die Frequenzerhöhung
könnte an der Bandbreite des Leistungstreibers für die Bewegung scheitern. Am
einfachsten scheint mir die Erhöhung der Amplitude.
- Wenn
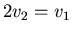 ist, dann ist auch
ist, dann ist auch
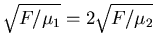 und damit
und damit
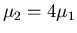 .
.
- Die Leistung
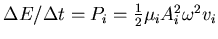
-
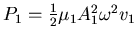
-
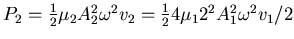
- Wir teilen die beiden Gleichungen und erhalten
-
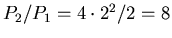
-
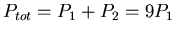
- reflektiert: 1/9
- transmittiert 8/9
- Die ursprüngliche Amplitude wird aus
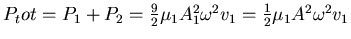 . Wir lösen nach
. Wir lösen nach 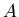 auf:
auf:
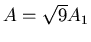
- reflektiert:
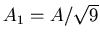
- transmittiert
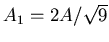
- In der Zeit
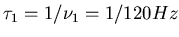 wandert die Störung auf der Saite um
wandert die Störung auf der Saite um
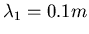 .
Die Geschwindigkeit ist
.
Die Geschwindigkeit ist
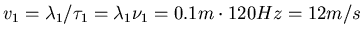
- Die Frequenz ist die gleiche.
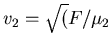 . Es ist auch
. Es ist auch
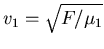 oder umgestellt
oder umgestellt
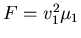 . Wir setzen ein und erhalten
. Wir setzen ein und erhalten
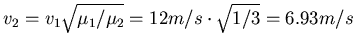
- Wellenlänge
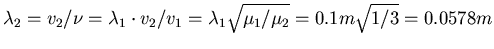
Wir lösen zuerst das zweite Problem, setzen aber für die Kopplung zwischen dem dritten
und dem ersten Pendel eine eigene Federkonstante 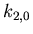 an.
an.
- Wir setzen
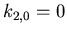 und bekommen die Lösungen
und bekommen die Lösungen
| No. |
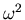 |
Anzahl |
Eigenvektor |
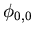 |
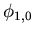 |
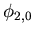 |
|---|
| 1 |
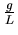 |
1 |
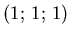 |
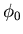 |
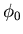 |
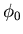 |
| 2 |
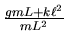 |
1 |
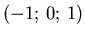 |
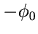 |
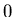 |
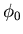 |
| 3 |
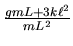 |
1 |
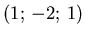 |
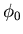 |
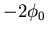 |
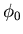 |
- Wir setzen
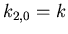 und bekommen die Lösungen
und bekommen die Lösungen
| No. |
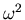 |
Anzahl |
Eigenvektor |
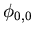 |
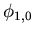 |
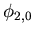 |
|---|
| 1 |
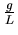 |
1 |
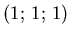 |
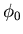 |
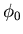 |
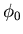 |
| 2 |
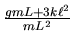 |
2 |
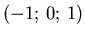
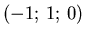 |
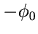 |
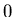 |
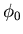 |
Hier ist die zweite Lösung entartet, da das Problem (die Anordnung der Pendel) eine
hohe Symmetrie aufweist. Eine Störung der Symmetrie hebt die Entartung auf und gibt
wieder drei Eigenfrequenzen.
- redwith(linalg):
Warning, new definition for norm
Warning, new definition for trace
- redMA :=
matrix(3,3,[A+B2+B,-B,-B2,-B,A+2*B,-B,-B2,-B,A+B+B2]);
- redeigenvalues(MA);
- redv := [eigenvectors(MA)];
- redA := g/L;
- redB:= (k*ell
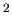 )/(m*L
)/(m*L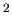 );
);
- redB2:= (k20*ell
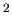 )/(m*L
)/(m*L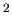 );
);
- redMB := matrix(3,3,[A+B2+B,-B,-B2,-B,A+2*B,-B,-B2,-B,A+B+B2]);
- redeigenvalues(MB);
- redvb := [eigenvectors(MB)];
- redB0_4:= (k*ell
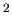 )/(m*L
)/(m*L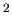 );
);
- redB1_4 := B0_4;
- redB2_4 := 0;
- redMB_4 := matrix(3,3,[A+B2_4+B0_4,-B0_4,-B2_4,-B0_4,A+B0_4+B1_4,-B1_4,-B2_4,-B1_4,A+B1_4+B2_4]);
- redeigenvalues(MB_4);
- redvb_4 := [eigenvectors(MB_4)];
- redB0_5:= (k*ell
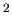 )/(m*L
)/(m*L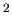 );
);
- redB1_5 := B0_5;
- redB2_5 := B0_5;
- redMB_5 :=
matrix(3,3,[A+B2_5+B0_5,-B0_5,-B2_5,-B0_5,A+B0_5+B1_5,-B1_5,-B2_5,-B1_5,A+B1_5+B2_5]);
- redeigenvalues(MB_5);
- redvb_5 := [eigenvectors(MB_5)];
Übungsblatt 14
Physik für Ingenieure 1
This document was generated using the
LaTeX2HTML translator Version 99.2beta8 (1.46)
Copyright © 1993, 1994, 1995, 1996,
Nikos Drakos,
Computer Based Learning Unit, University of Leeds.
Copyright © 1997, 1998, 1999,
Ross Moore,
Mathematics Department, Macquarie University, Sydney.
The command line arguments were:
latex2html D:_Ing_11414
The translation was initiated by marti on 2002-02-04


Up: Physik 1 für Ingenieure
Othmar Marti
Experimentelle Physik
Universiät Ulm
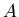 besass.
besass.
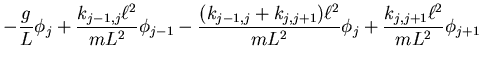
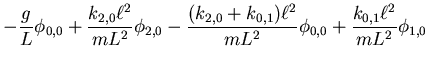
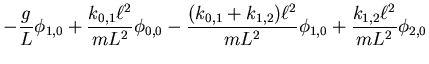
![\begin{displaymath}
\mathit{MA} := \left[ {\begin{array}{ccc} A + \mathit{B2} +...
...mathit{B2} & - B & A + \mathit{B2} + B
\end{array}}
\right]
\end{displaymath}](img81.gif)
![\begin{displaymath}
\mathit{MB} := \left[ {\begin{array}{ccc} {\displaystyle \f...
...rac {k\,
\mathit{ell}^{2}}{m\,L^{2}}}
\end{array}}
\right]
\end{displaymath}](img88.gif)
![\begin{eqnarray*}
\lefteqn{\mathit{vb} := [[{\displaystyle \frac {g\,m\,L + 2\,...
...m\,
L^{2}}} , \,1, \,\{[1, \,-2, \,1]\}]]\mbox{\hspace{134pt}}
\end{eqnarray*}](img90.gif)
![\begin{displaymath}
\mathit{MB\_4} := \left[ {\begin{array}{ccc} {\displaystyle...
...frac {k\,\mathit{ ell}^{2}}{m\,L^{2}}}
\end{array}}
\right]
\end{displaymath}](img94.gif)
![\begin{eqnarray*}
\lefteqn{\mathit{vb\_4} := [[{\displaystyle \frac {g}{L}} , \...
...m\,L^{
2}}} , \,1, \,\{[-1, \,0, \,1]\}]]\mbox{\hspace{106pt}}
\end{eqnarray*}](img96.gif)
![\begin{displaymath}
\mathit{MB\_5} := \left[ {\begin{array}{ccc} {\displaystyle...
...frac {k\, \mathit{ell}^{2}}{m\,L^{2}}}
\end{array}}
\right]
\end{displaymath}](img100.gif)