

Up: Physik 1 für Ingenieure
Übungsblatt 2
Physik für Ingenieure 1
Othmar Marti, (othmar.marti@physik.uni-ulm.de)
23. 10. 2001
Kinematik
- Ein Massepunkt bewegt sich nach der Gleichung
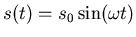 . Konstruieren sie und berechnen sie die
momentane Geschwindigkeit und die momentane Beschleunigung für die Zeiten
. Konstruieren sie und berechnen sie die
momentane Geschwindigkeit und die momentane Beschleunigung für die Zeiten
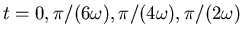 .
.
- Eine gerade Bahnstrecke geht in einen Kreisbogen mit
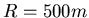 über. Stellen Sie den Ort, die Geschwindigkeit
und die Beschleunigung graphisch und qualitativ dar, wenn der Zug mit einer
konstanten Geschwindigkeit von
über. Stellen Sie den Ort, die Geschwindigkeit
und die Beschleunigung graphisch und qualitativ dar, wenn der Zug mit einer
konstanten Geschwindigkeit von 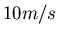 fährt. Betrachten Sie die
fährt. Betrachten Sie die 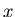 - und
- und 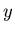 -Komponenten des Ortes, der
Geschwindigkeit und der Beschleunigung kurz vor und kurz nach dem Übergang von einer linearen Bewegung in eine
Kreisbewegung.
Was schliessen Sie aus Ihrer Darstellung über den Fahrkomfort?
-Komponenten des Ortes, der
Geschwindigkeit und der Beschleunigung kurz vor und kurz nach dem Übergang von einer linearen Bewegung in eine
Kreisbewegung.
Was schliessen Sie aus Ihrer Darstellung über den Fahrkomfort?
- Wenn Sie die Luftreibung vernachlässigen können und wenn Sie einem Körper eine Maximalgeschwindigkeit
von 10 m/s geben können, was ist der optimale Wurfwinkel und die Wurfweite?
Wie lautet die Formel für die Weite, wenn Sie
berücksichtigen, dass Sie 2 m gross sind, und dass deshalb Ihre Hand diese Höhe über Boden hat?
Verwenden Sie für
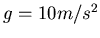 .
.
- Ein Flugzeug soll auf einem Kurs Richtung Norden fliegen. Seine Geschwindigkeit gegenüber der Luft ist
200 m/s. In welche Richtung muss die Nase des Flugzeuges zeigen, wenn die Luft mit 25 m/s sich von Westen gegen
Osten bewegt. Was ist die Geschwindigkeit über Grund?
- Ein Schwimmwettbewerb zwischen zwei auf die zehntausendstel Sekunde über 100 m gleich schnellen Schwimmerinnen
(Zeit für 100 m: 50 s) soll auf der Donau ausgetragen werden. Die eine Schwimmstrecke ist parallel zum Ufer
und 100 m lang, die andere ist senkrecht zum Ufer und auch 100 m lang. Gemessen wird die Zeit um die jeweilige
Strecke in beide Richtungen zu durchschwimmen. Wer erreicht das Ziel zuerst, wenn die Donau mit
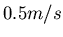 gleichmässig auf der ganzen Breite fliesst?
gleichmässig auf der ganzen Breite fliesst?
- Freiwillig: Lösen sie eine oder mehrere Aufgaben aus dem Tipler, Seiten 66-70.
-
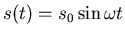
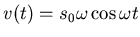
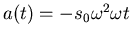
![\includegraphics[width=0.6\textwidth]{Bilder/aufg1a.eps}](img24.gif)
![\includegraphics[width=0.6\textwidth]{Bilder/aufg1b.eps}](img25.gif)
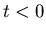
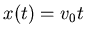 ,
, 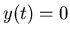
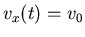 ,
, 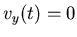
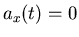 ,
, 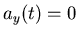
Im Kreisbogen
Winkel:
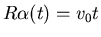 , also
, also
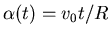
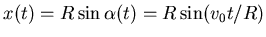 ,
,
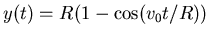
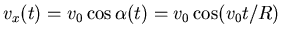 ,
,
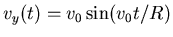
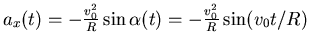 ,
,
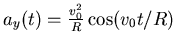
Zahlenwerte der Vorfaktoren: 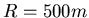 ,
, 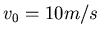 ,
,
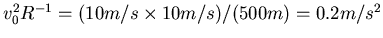
![\includegraphics[width=0.6\textwidth]{Bilder/aufg2a.eps}](img43.gif)
![\includegraphics[width=0.6\textwidth]{Bilder/aufg2b.eps}](img44.gif)
![\includegraphics[width=0.6\textwidth]{Bilder/aufg2c.eps}](img45.gif)
-
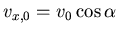
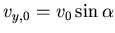
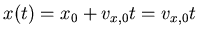
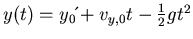
Landung, wenn 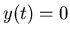 , löse
, löse
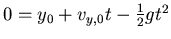
Erster Teil, setze 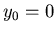 . Dann ist:
. Dann ist:
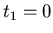 ,
,
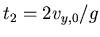
Einsetzen in 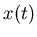
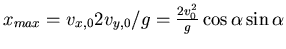
Mit
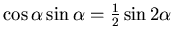 wird
wird
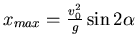
Man erhält die maximale Reichweite für
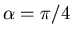
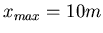
Teil 2: nun 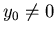 .
.
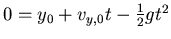
Also
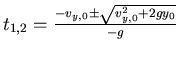
Wir erhalten die maximale Flugdauer für das ''-'' - Zeichen
![$t_{max} = \frac{v_{y,0}}{g} + \sqrt{\left(\frac{v_{y,0}}{g}\right)^2+2 \frac{y_0}{g}}=
\frac{v_{y,0}}{g}\left[1+\sqrt{1+2\frac{y_0 g}{v_{y,0}^2}}\right]$](img62.gif)
Einsetzten in 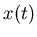 ergibt:
ergibt:
![$x_{max} = \frac{v_{x,0} v_{y,0}}{g}\left[1+\sqrt{1+2\frac{y_0 g}{v_{y,0}^2}}\right]\approx
\frac{v_{x,0} v_{y,0}}{g}\left[2+\frac{y_0 g}{v_{y,0}^2}\right]$](img63.gif)
Wir rechnen nun noch den Winkel aus:
![$x_{max} = \frac{v_0^2 \cos\alpha\sin\alpha}{g}\left[1+\sqrt{1+2\frac{y_0 g}{v_0...
...rac{v_0^2\cos\alpha\sin\alpha}{g}\left[2+\frac{y_0 g}{v_y^2\sin^2\alpha}\right]$](img64.gif)
Nun müsste das Maximum dieser Funktion gesucht werden. Da der Vorfaktor von 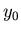 grösser
null ist, ist die Reichweite in jedem Falle grösser bei einem flacheren Abwurfwinkel.
grösser
null ist, ist die Reichweite in jedem Falle grösser bei einem flacheren Abwurfwinkel.
Grafische Darstellung:
![\includegraphics[width=0.6\textwidth]{Bilder/reichweite.eps}](img66.gif)
Excel-Datei für Rechnung: (wurf.xls [Excel 97/2000])
- Es gilt:
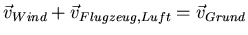
Dies ist ein rechtwinkliges Dreieck, also
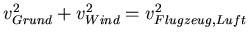
Mit den Zahlenwerten bekommt man
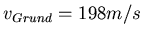
Winkel:
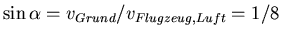 , also
, also
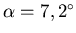
- Die Lösung der Aufgabe 4 ist auch die Lösung des Teils 2, die Donau zweimal überqueren.
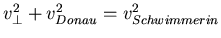
Gesamtzeit (s: Strecke):
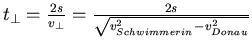
Parallel zur Donau wird einmal mi und einmal gegen den Strom geschwommen.
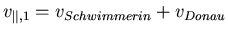 ,
,
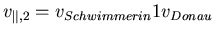
 ,
,

Also:
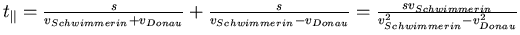
Eingesetzt:
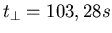 ,
,
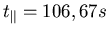
PS: Diese Überlegung wird zur Herleitung der Lorentz-Kontraktion in der speziellen Relativitätstheorie
verwendet.
Übungsblatt 2
Physik für Ingenieure 1
This document was generated using the
LaTeX2HTML translator Version 99.2beta8 (1.46)
Copyright © 1993, 1994, 1995, 1996,
Nikos Drakos,
Computer Based Learning Unit, University of Leeds.
Copyright © 1997, 1998, 1999,
Ross Moore,
Mathematics Department, Macquarie University, Sydney.
The command line arguments were:
latex2html D:_Ing_122
The translation was initiated by marti on 2001-12-03


Up: Physik 1 für Ingenieure
Othmar Marti
Experimentelle Physik
Universiät Ulm
![\includegraphics[width=0.6\textwidth]{Bilder/aufg1a.eps}](img24.gif)
![\includegraphics[width=0.6\textwidth]{Bilder/aufg1b.eps}](img25.gif)
![\includegraphics[width=0.6\textwidth]{Bilder/aufg2a.eps}](img43.gif)
![\includegraphics[width=0.6\textwidth]{Bilder/aufg2b.eps}](img44.gif)
![\includegraphics[width=0.6\textwidth]{Bilder/aufg2c.eps}](img45.gif)
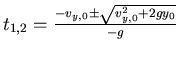
![$t_{max} = \frac{v_{y,0}}{g} + \sqrt{\left(\frac{v_{y,0}}{g}\right)^2+2 \frac{y_0}{g}}=
\frac{v_{y,0}}{g}\left[1+\sqrt{1+2\frac{y_0 g}{v_{y,0}^2}}\right]$](img62.gif)
![$x_{max} = \frac{v_{x,0} v_{y,0}}{g}\left[1+\sqrt{1+2\frac{y_0 g}{v_{y,0}^2}}\right]\approx
\frac{v_{x,0} v_{y,0}}{g}\left[2+\frac{y_0 g}{v_{y,0}^2}\right]$](img63.gif)
![$x_{max} = \frac{v_0^2 \cos\alpha\sin\alpha}{g}\left[1+\sqrt{1+2\frac{y_0 g}{v_0...
...rac{v_0^2\cos\alpha\sin\alpha}{g}\left[2+\frac{y_0 g}{v_y^2\sin^2\alpha}\right]$](img64.gif)
![\includegraphics[width=0.6\textwidth]{Bilder/reichweite.eps}](img66.gif)