

Up: Physik 1 für Ingenieure
Übungsblatt 3
Physik für Ingenieure 1
Othmar Marti, (othmar.marti@physik.uni-ulm.de)
3. Dezember 2001
Kinematik
Dynamik
- Elektronen und andere geladene Teilchen bewegen sich auf Spiralbahnen durch Magnetfelder. Die Bahnkurve ist durch
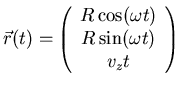 . Berechnen Sie
die Geschwindigkeit und die Beschleunigung.
. Berechnen Sie
die Geschwindigkeit und die Beschleunigung.
- Bei einer Kirmes-Bahn sei der Ort als Funktion der Zeit durch
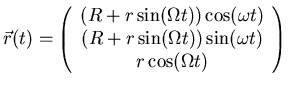 . Berechnen Sie wieder Geschwindigkeit
und Beschleunigung.
. Berechnen Sie wieder Geschwindigkeit
und Beschleunigung.
- Drehen Sie den Vektor
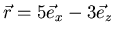 zuerst um
zuerst um 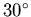 um die y-Achse und
dann um
um die y-Achse und
dann um 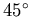 um die z-Achse.
um die z-Achse.
- Auf ein Förderband (Geschwindigkeit: 1 m/s) fallen pro Sekunde 10 kg Schotter. Berechne die Kraft,
die benötigt wird, um eine konstante Geschwindigkeit aufrecht zu erhalten.
- Sie fahren mit der Geschwindigkeit
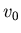 senkrecht auf ein unendlich ausgedehntes Hindernis zu.
Die maximale Kraft, die über die
Räder auf den Boden übertragen werden kann, ist
senkrecht auf ein unendlich ausgedehntes Hindernis zu.
Die maximale Kraft, die über die
Räder auf den Boden übertragen werden kann, ist 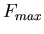 . Ihr Auto hat die Masse
. Ihr Auto hat die Masse 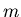 . Berechnen Sie den
kürzesten Bremsweg
. Berechnen Sie den
kürzesten Bremsweg 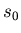 (Die Trägheitskraft ist
(Die Trägheitskraft ist 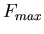 ) und den minimal nötigen Radius
) und den minimal nötigen Radius 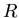 um eine Kurve zu
fahren (wieder soll die Zentripetalkraft gleich
um eine Kurve zu
fahren (wieder soll die Zentripetalkraft gleich 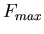 sein).
sein).
Was wäre das Resultat, wenn das Hindernis die Ausdehnung 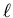 von ihrer ursprünglichen Fahrachse hätte?
von ihrer ursprünglichen Fahrachse hätte?
Was folgt für ihre Fahrpraxis aus den Resultaten?
- Ort:
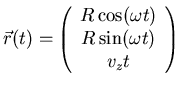
Geschwindigkeit:
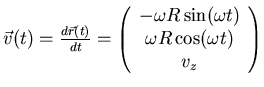
Beschleunigung:
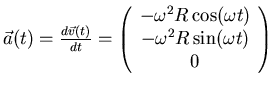
- Ort:
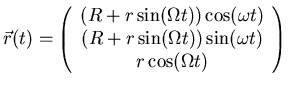 .
.
Geschwindigkeit:
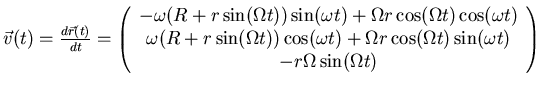
Beschleunigung:
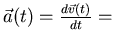
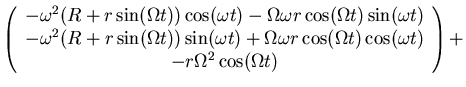
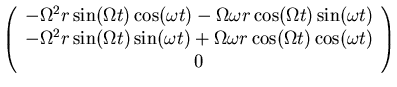 =
=
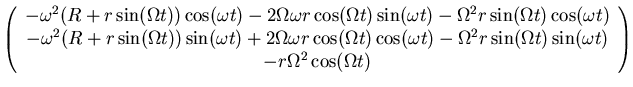
-
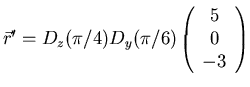
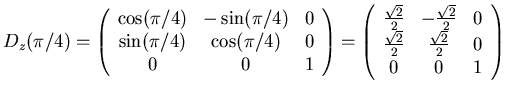
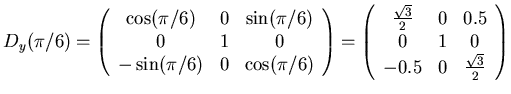
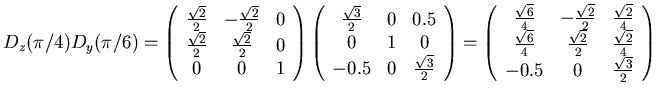
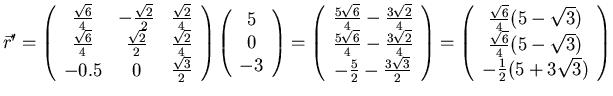
- 2. Newtonsches Axiom:
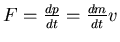 (da v= const).
(da v= const).
Einsetzen:
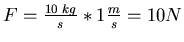
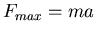 oder
oder
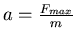 . Einsetzen in die Gleichung
. Einsetzen in die Gleichung 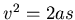 ergibt
ergibt
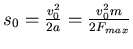
Wir verwenden
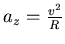 und erhalten
und erhalten
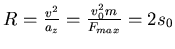
Wir betrachten die Trajektorie des Autos:
![\includegraphics[width=0.6\textwidth]{Bremse.eps}](img32.gif)
Es gilt:
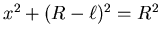 . Aufgelöst nach x:
. Aufgelöst nach x:
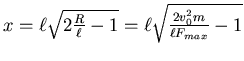 .
.
Wenn der Abstand 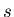 zum Hindernis grösser als
zum Hindernis grösser als 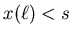 ist, kann das Hindernis umfahren werden.
ist, kann das Hindernis umfahren werden.
Übungsblatt 3
Physik für Ingenieure 1
This document was generated using the
LaTeX2HTML translator Version 99.2beta8 (1.46)
Copyright © 1993, 1994, 1995, 1996,
Nikos Drakos,
Computer Based Learning Unit, University of Leeds.
Copyright © 1997, 1998, 1999,
Ross Moore,
Mathematics Department, Macquarie University, Sydney.
The command line arguments were:
latex2html D:_Ing_133
The translation was initiated by marti on 2001-12-03


Up: Physik 1 für Ingenieure
Othmar Marti
Experimentelle Physik
Universiät Ulm
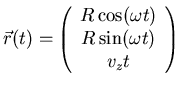 . Berechnen Sie
die Geschwindigkeit und die Beschleunigung.
. Berechnen Sie
die Geschwindigkeit und die Beschleunigung.
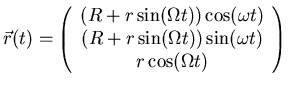 . Berechnen Sie wieder Geschwindigkeit
und Beschleunigung.
. Berechnen Sie wieder Geschwindigkeit
und Beschleunigung.
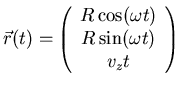 . Berechnen Sie
die Geschwindigkeit und die Beschleunigung.
. Berechnen Sie
die Geschwindigkeit und die Beschleunigung.
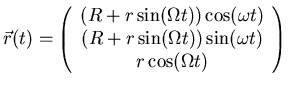 . Berechnen Sie wieder Geschwindigkeit
und Beschleunigung.
. Berechnen Sie wieder Geschwindigkeit
und Beschleunigung.
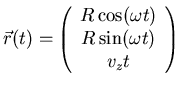
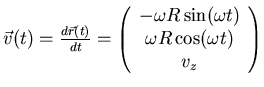
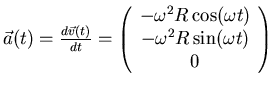
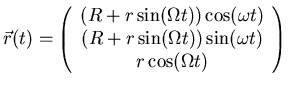 .
.
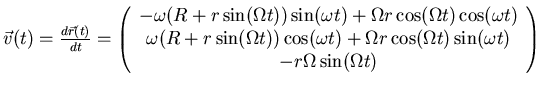
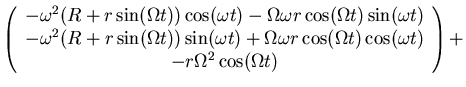
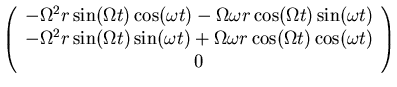 =
=
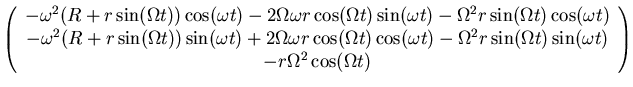
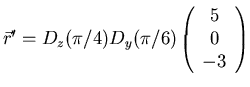
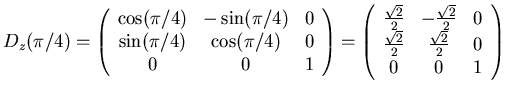
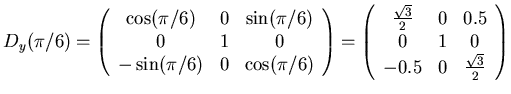
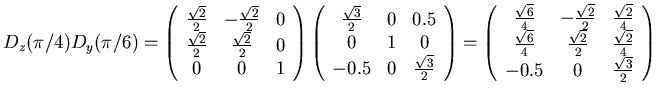
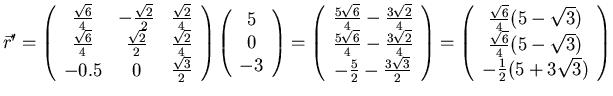
![\includegraphics[width=0.6\textwidth]{Bremse.eps}](img32.gif)
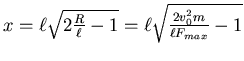 .
.