

Up: Physik 1 für Ingenieure
Übungsblatt 9
Physik für Ingenieure 1
Othmar Marti, (othmar.marti@physik.uni-ulm.de)
11. 12. 2001
![\framebox[0.8\textwidth]{\begin{minipage}{0.75\textwidth} \textbf{Mitteilung} ...
...in einer noch anzugebenden Weise bekannt
gemacht.)
\end{itemize}\end{minipage}}](img1.gif)
Gravitation, Elastizitätslehre,
Spezielle Relativitätstheorie,
PDF-Datei
- Betrachten Sie einen Würfel der Kantenlänge
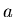 mit der Dichte
mit der Dichte
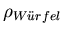 ,
der an der Erdoberfläche in ein fluides Medium der Dichte
,
der an der Erdoberfläche in ein fluides Medium der Dichte 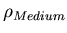 eingebettet ist.
eingebettet ist.
- Berechnen Sie die Kräfte auf den Würfel.
- Bedingung für statisches Gleichgewicht, sinken und steigen.
- Um wie viel nimmt sein Volumen ab?
- Aus einem Federdraht mit dem Durchmesser
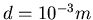 ,
,
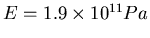 ,
,
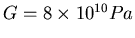 ,
,
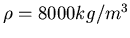 wird eine Spiralfeder mit dem
Durchmesser von
wird eine Spiralfeder mit dem
Durchmesser von 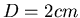 gewickelt. Die Windungen liegen, ohne Vorspannung, dicht
aneinander. Die Länge der Schraubenfeder sei
gewickelt. Die Windungen liegen, ohne Vorspannung, dicht
aneinander. Die Länge der Schraubenfeder sei 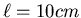 . An den Enden wird der
Federdraht zur Mitte der Feder gebracht und die Kraft dort angewandt. Berechnen
Sie die Federkonstante des Drahtes.
. An den Enden wird der
Federdraht zur Mitte der Feder gebracht und die Kraft dort angewandt. Berechnen
Sie die Federkonstante des Drahtes.
- Die E-Saite einer Violine stehe unter einer Zugkraft von
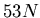 . Ihr
Durchmesser betrage
. Ihr
Durchmesser betrage 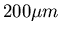 , ihre Länge sei
, ihre Länge sei 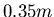 und
und 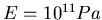 . Bestimmen Sie
. Bestimmen Sie
- die Länge der Saite ohne Spannung
- die zur Spannung der Saite nötige Arbeit
- Bei der Gravitationswaage wurde eine Auslenkung des Lichtstrahls von 5 cm
im Abstand von 10 m gemessen. Die kleinen Massen (
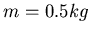 ) seien an einem Draht der Dicke
) seien an einem Draht der Dicke 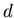 und der Länge
und der Länge 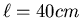 im Abstand
im Abstand 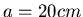 aufgehängt, der Spiegel befinde sich in der Mitte des
Drahtes. Die grossen Massen (
aufgehängt, der Spiegel befinde sich in der Mitte des
Drahtes. Die grossen Massen (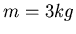 seien zuerst im Abstand von jeweils
seien zuerst im Abstand von jeweils 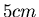 von
den kleinen Massen und werden, um den beobachteten Ausschlag zu erzeugen, entfernt.
Schlagen sie eine Drahtdicke für einen Eisendraht vor!
von
den kleinen Massen und werden, um den beobachteten Ausschlag zu erzeugen, entfernt.
Schlagen sie eine Drahtdicke für einen Eisendraht vor!
- Wir zerlegen die Flüssigkeit in Schichten der Dicke
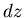 . Jedes Volumenelement in dieser Schicht
wird von der Erde mit
. Jedes Volumenelement in dieser Schicht
wird von der Erde mit
 angezogen.
angezogen.
- Das nach unten folgende Volumenelement muss zusätzlich noch die Last des über
ihm liegenden Volumenelements tragen: Integration.
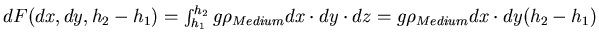 . Wenn über dem Würfel mit der Seitenfläche
. Wenn über dem Würfel mit der Seitenfläche 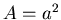 das
Medium die Höhe
das
Medium die Höhe 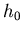 hat, ist die Kraft von oben auf den Würfel:
hat, ist die Kraft von oben auf den Würfel:
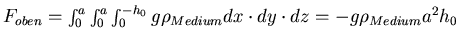 . Von unten wirkt die Kraft
. Von unten wirkt die Kraft
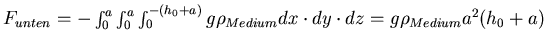 . Netto ist die Auftriebskraft
. Netto ist die Auftriebskraft
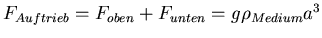 . Die seitlichen
Kräfte heben sich auf, da der hydrostatische Druck nur von der Tiefe
. Die seitlichen
Kräfte heben sich auf, da der hydrostatische Druck nur von der Tiefe
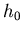 abhängt.
abhängt.
- Der Würfel selber wird mit
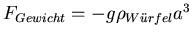 von der Erde angezogen. Die
Summe aller äusseren Kräfte ist
von der Erde angezogen. Die
Summe aller äusseren Kräfte ist
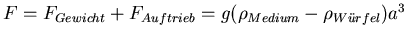 . Wenn
. Wenn
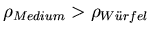 ist, steigt der Würfel an die
Oberfläche des Mediums, bei
ist, steigt der Würfel an die
Oberfläche des Mediums, bei
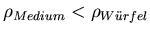 sinkt er
und bei
sinkt er
und bei
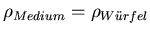 ist er im indifferenten
Gleichgewicht.
ist er im indifferenten
Gleichgewicht.
- Auf eine zur Oberfläche des Mediums parallele Schicht des Würfels der
Dicke
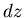 wirkt der Druck
wirkt der Druck
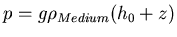 . Das Volumen der
Schicht ist
. Das Volumen der
Schicht ist 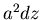 . Es wird um
. Es wird um
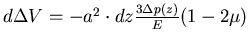 komprimiert.
Insgesamt ist
komprimiert.
Insgesamt ist
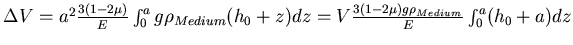
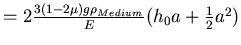
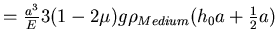 .
.
- Die Spiralfeder hat
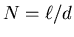 Windungen. Die Drahtlänge für eine Umdrehung ist
Windungen. Die Drahtlänge für eine Umdrehung ist
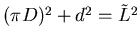 . Die Drahtlänge ist
. Die Drahtlänge ist
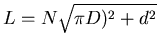 ,
auf dieser Länge wird der Draht durch das Drehmoment
,
auf dieser Länge wird der Draht durch das Drehmoment 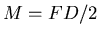 verdrillt. Wir
verwenden
verdrillt. Wir
verwenden
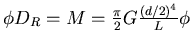 Der Winkel
Der Winkel 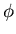 ist durch die folgende Überlegung gegeben: Der gesamte Drehwinkel des Drahtes ist
ist durch die folgende Überlegung gegeben: Der gesamte Drehwinkel des Drahtes ist
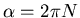 . Wird die Feder um
. Wird die Feder um 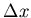 verlängert, wird dieses
verlängert, wird dieses 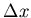 auf jede Windung aufgeteilt. Also ist
auf jede Windung aufgeteilt. Also ist
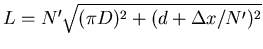 und damit
und damit
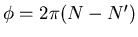 . Mit
. Mit
![$N'^2[(\pi D)^2 + (d+\Delta x/N')^2] = N^2[(\pi D)^2 +
d^2]$](img50.gif) . Damit ist auch
. Damit ist auch
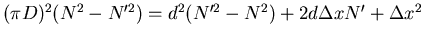 . Diese Gleichung wird nach
. Diese Gleichung wird nach 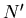 aufgelöst. Man löst die quadratische
Gleichung und linearisiert die kleinen Terme mit
aufgelöst. Man löst die quadratische
Gleichung und linearisiert die kleinen Terme mit 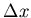 und erhält:
und erhält:
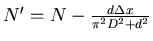 und damit
und damit
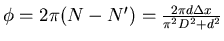
Es ist also
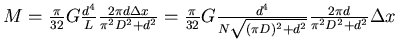
![$= \frac{\pi^2}{16}G d^5 N^{-1} [(\pi D)^2 + d^2]^{-3/2}\Delta
x$](img56.gif) .
.
Nun ist aber auch 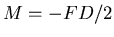 und damit
und damit
![$ \Delta -F D/2 = \frac{\pi^2}{16}G d^5 N^{-1} [(\pi D)^2 + d^2]^{-3/2}\Delta
x$](img58.gif) und somit
und somit
![$ \Delta F = -\frac{\pi^2}{8}G d^5 D^{-1} N^{-1} [(\pi D)^2 + d^2]^{-3/2}\Delta
x$](img59.gif) .
.
Mit
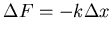 ist
ist
![$ k = \frac{\pi^2}{8}G d^5 D^{-1} N^{-1} [(\pi D)^2 + d^2]^{-3/2}$](img61.gif) die Federkonstante
des Spiralfeder.
die Federkonstante
des Spiralfeder.
- Es ist
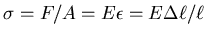 .
Also ist
.
Also ist
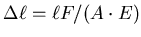 .
Bekannt ist
.
Bekannt ist
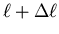 und
gesucht ist
und
gesucht ist 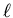 .
Es ist
.
Es ist
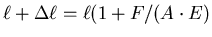
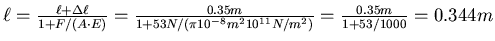
- Die Federkonstante dieser Saite ist
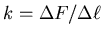
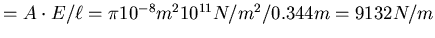 .
Die Spannarbeit ist
.
Die Spannarbeit ist
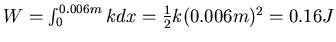 .
.
- Die Winkelauslenkung
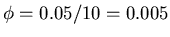 . Der Draht wird insgesamt um
. Der Draht wird insgesamt um
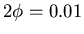 verdrillt. Das Richtmoment des Drahtes ist
verdrillt. Das Richtmoment des Drahtes ist
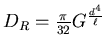 . Wir haben
. Wir haben
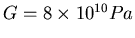 und eine Drahtlänge
von
und eine Drahtlänge
von 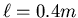 . Die Gravitationskraft einer Kugel auf die zweite ist
. Die Gravitationskraft einer Kugel auf die zweite ist
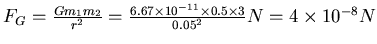 Die gesamte Kraftänderung ist vier mal so gross (je 2 Kugeln und
diese auf zwei gegenüberliegenden Seiten)
Die gesamte Kraftänderung ist vier mal so gross (je 2 Kugeln und
diese auf zwei gegenüberliegenden Seiten)
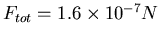 . Das durch
die Gravitation ausgeübte Drehmoment ist
. Das durch
die Gravitation ausgeübte Drehmoment ist
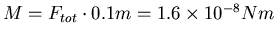
Wir haben auch 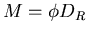 und damit
und damit
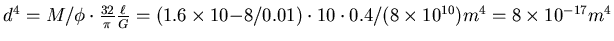 und damit
und damit 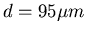 .
.
Die Zugkraft an dem Draht ist 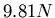 und die Spannung damit
und die Spannung damit
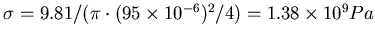 , ein Wert der nur unwesentlich
unter der Fliessgrenze für Federstahl (
, ein Wert der nur unwesentlich
unter der Fliessgrenze für Federstahl (
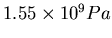 ) ist.
) ist.
Die Gravitationswaage ist ein Gerät, das an der Grenze des technisch machbaren liegt.
Übungsblatt 9
Physik für Ingenieure 1
This document was generated using the
LaTeX2HTML translator Version 99.2beta8 (1.46)
Copyright © 1993, 1994, 1995, 1996,
Nikos Drakos,
Computer Based Learning Unit, University of Leeds.
Copyright © 1997, 1998, 1999,
Ross Moore,
Mathematics Department, Macquarie University, Sydney.
The command line arguments were:
latex2html D:_Ing_199
The translation was initiated by marti on 2001-12-18


Up: Physik 1 für Ingenieure
Othmar Marti
Experimentelle Physik
Universiät Ulm
![\framebox[0.8\textwidth]{\begin{minipage}{0.75\textwidth} \textbf{Mitteilung} ...
...in einer noch anzugebenden Weise bekannt
gemacht.)
\end{itemize}\end{minipage}}](img1.gif)
![\framebox[0.8\textwidth]{\begin{minipage}{0.75\textwidth} \textbf{Mitteilung} ...
...in einer noch anzugebenden Weise bekannt
gemacht.)
\end{itemize}\end{minipage}}](img1.gif)
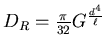 . Wir haben
. Wir haben