
Die klassische Definition eines Wärmereservoirs lautet:
Die statistische Betrachtung geht so: Wir haben zwei Systeme A und A′ im Kontakt. Das System A′ ist ein Wärmebad oder Wärmereservoir, wenn T′ sich kaum ändert bei der Wärmezufuhr Q. Die kann in einer Gleichung so geschrieben werden:
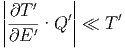 | (2.2) |
Daraus folgt
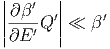 | (2.3) |
dann sollte auch
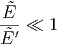 |
sein.
Sei nun Ω′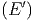 die Anzahl der zugänglichen Zustände von
A′ im Energieintervall von E bis E + δE. Das System
A′ absorbiere die Energie ΔE′ = Q′. Dann lautet die
Taylor-Entwicklung
die Anzahl der zugänglichen Zustände von
A′ im Energieintervall von E bis E + δE. Das System
A′ absorbiere die Energie ΔE′ = Q′. Dann lautet die
Taylor-Entwicklung
ln Ω′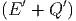 - ln Ω′ - ln Ω′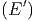 | = 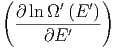 Q′ + Q′ + 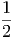 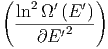 Q′2 + O Q′2 + O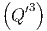 | ||
= β′Q′ + 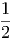 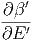 Q′2 + O Q′2 + O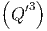 | (2.4) |
Die Terme 2. und höherer Ordnung können vernachlässigt werden, da mit Gleichung (2.3) gilt
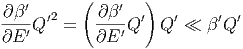 |
Damit bekommen wir
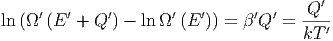 | (2.5) |
oder
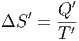 | (2.6) |
wenn die Wärmemenge Q′ mit einem Wärmebad ausgetauscht wird.
Eine analoge Rechnung gilt auch für infinitesimale Wärmemengen δQ.
Sei δQ « E. Dann haben wir
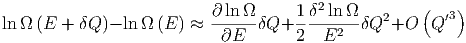 | (2.7) |
und wieder
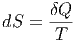 | (2.8) |
Diese Gleichung hatten wir schon bei der nichtstatistischen Betrachtung der Entropie verwendet. Es ist doch beruhigend, dass die statistische Betrachtung auf die gleichen Gesetze wie die klassische Betrachtung führt.
 Lizenzinformationen
Lizenzinformationen