__________________________________________________________________________
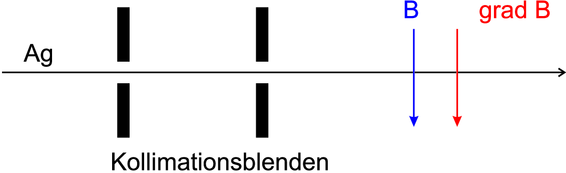
Versuchsaufbau Stern-Gerlach-Versuch
_____________________________________________________________________

Wenn Atome magnetische Momente haben, werden sie in einem Magnetfeldgradienten abgelenkt. In einem homogenen Magnetfeld jedoch gibt es keine Ablenkung. Im Experiment von Stern und Gerlach wurden neutrale Silberatome durch ein inhomogenes Magnetfeld geschickt.
__________________________________________________________________________

Versuchsaufbau Stern-Gerlach-Versuch
_____________________________________________________________________
Abbildung 6.4.1 zeigt den symbolischen Aufbau. In einem
homogenen Magnetfeld wirkt auf ein magnetisches Moment
keine Kraft. Wenn das magnetische Moment 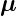 nicht
parallel zur magnetischen Induktion
nicht
parallel zur magnetischen Induktion 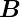 ist, präzediert das
magnetische Moment
ist, präzediert das
magnetische Moment 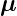 =
= 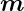 A = I·A·
A = I·A·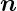 wegen dem
Drehmoment
wegen dem
Drehmoment 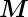 =
= 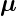 ×
×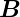 . Die magnetische Lageenergie
ist
. Die magnetische Lageenergie
ist
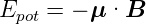 | (6.1) |
Die Kraft auf einen Dipol im Gradientenfeld ist
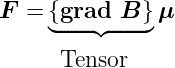
Bei einem üblichen thermodynamischen System erwartet
man, dass die magnetischen Momente 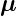 beliebig zu
beliebig zu 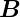 orientiert sind.
orientiert sind.
__________________________________________________________________________
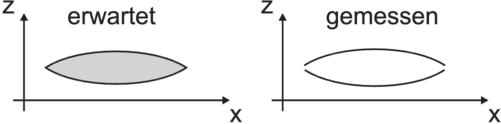
Skizze: Erwartete (links) und gemessene Verteilung der Elektronen beim Stern-Gerlach-Versuch.
_____________________________________________________________________
Abbildung 6.4.1 zeigt eine Skizze der erwarteten und, rechts, der gemessenen Verteilung. Die Ergebnisse zeigen, dass die z-Komponente des magnetischen Momentes der Silberatome im Magnetfeld quantisiert ist.
Um zu einem Ausdruck für den Drehimpulsoperator zu kommen, betrachten wir den Strom in einem Atom.
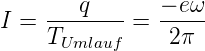 | (6.2) |
Der Drehimpuls ist
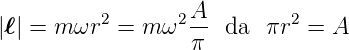 | (6.3) |
Der Drehimpuls ist also proportional zu der Fläche A des Kreisstromes. Das magnetische Moment ist
Das Minuszeichen rührt von der negativen Elementarladung her. Setzt man den Betrag des Drehimpulses gleich dem reduzierten Planckschen Wirkungsquantum,
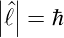
erhält man das Bohrsche Magneton
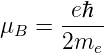 | (6.6) |
__________________________________________________________________________
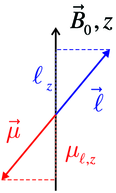
Zusammenhang zwischen Drehimpuls und magnetischem Moment
_____________________________________________________________________
Das magnetische Moment des Elektrons ist (siehe Abbildung 6.4.1.1)
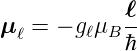 | (6.7) |
Die Grösse gℓ ist der sogenannte g-Faktor. Beim magnetischen Moment eines Kreisstromes ist g = 1. Die Eigenwerte des magnetischen Momentes sind:
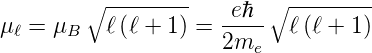 | (6.8) |
Die Drehimpulsänderung bei der Präzession ist
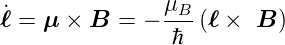 | (6.9) |
Die Frequenz dieser Präzession ist die Larmor-Frequenz
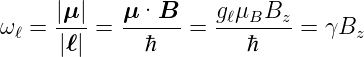 | (6.10) |
Hier ist γ das gyromagnetische Verhältnis.
 Lizenzinformationen
Lizenzinformationen