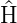 hat die Form
hat die Form
Wenn die potentielle Energie V (x) eine quadratisch von
x abhängt ist die Bewegung des Teilchens beschränkt und
analog zum Fall eines klassischen harmonischen Oszillators.
Der Operator 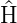 hat die Form
hat die Form
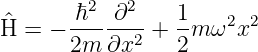 | (5.1) |
mit der potentiellen Energie
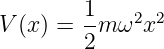 | (5.2) |
Die Lösungen der Schrödingergleichung sind stationär und haben, dem Separationsansatz entsprechend, die Form
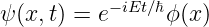 | (5.3) |
Damit können wir die zeitunabhängige Schrödingergleichung verwenden
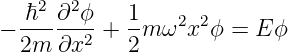 | (5.4) |
__________________________________________________________________________
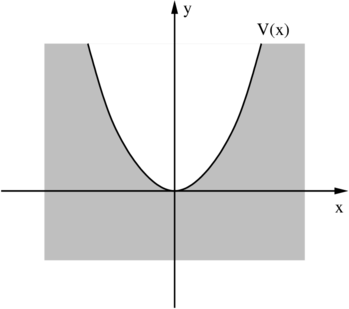
Mögliche Energiefunktion eines harmonischen Oszillators.
_____________________________________________________________________
Wir definieren drei Parameter und ersetzen die Variable x durch u
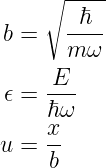 | (5.5) |
Die Gleichung 5.4 lautet dann (siehe auch [CH67, p. 280, Kap. 5, §10])
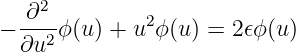 | (5.6) |
Um die Eigenfunktionen ϕn und die Eigenwerte 𝜖n (oder En) zu finden, definieren wir die folgenden Operatoren:
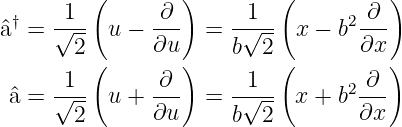 | (5.7) |
Die Operatoren 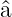 † und
† und 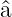 sind nicht hermitisch (also nicht
selbstadjungiert). Sie sind aber adjungiert zueinander.
Deshalb kann man mit
sind nicht hermitisch (also nicht
selbstadjungiert). Sie sind aber adjungiert zueinander.
Deshalb kann man mit
formal schreiben
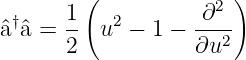 | (5.9) |
und mit Gleichung (5.6)
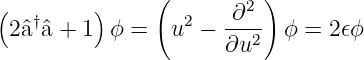 | (5.10) |
und
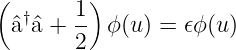 | (5.11) |
Wir definieren einen neuen Hamiltonoperator (Faktor 2
Unterschied zum Original) mit den Operatoren 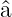 und
und
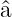 †
†
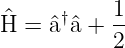 | (5.12) |
Weiter haben wir
Der Kommutator der Operatoren 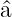 und
und 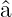 † hat den Wert
(Gleichungen (5.8) und (5.13))
† hat den Wert
(Gleichungen (5.8) und (5.13))
![[ †] † †
^a,^a = ^a^a − ^a ^a = 1](ap-2019573x.png) | (5.14) |
Die Eigenschaften des Kommutators zeigen, dass
![[^a,^a ] = 0](ap-2019574x.png) | (5.15) |
und
![[ ]
^a †,^a † = 0](ap-2019575x.png) | (5.16) |
Wir wollen nun untersuchen, wie die Gleichung (5.11) sich
ändert, wenn wir sie von links mit 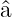 oder
oder 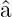 † multiplizieren.
Wir schreiben Gleichung (5.11) um
† multiplizieren.
Wir schreiben Gleichung (5.11) um
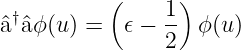 | (5.17) |
Multiplizieren wir Gleichung (5.17) von links mit 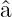 und
verwenden Gleichung (5.14) erhalten wir
und
verwenden Gleichung (5.14) erhalten wir
Wenn ϕ(u) eine Lösung der Gleichung (5.17)
mit dem Eigenwert (𝜖 − 1∕2) ist, ist 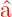 ϕ(u) eine
Lösung der gleichen Gleichung (5.17), aber mit dem
Eigenwert ϕ(u) eine
Lösung der gleichen Gleichung (5.17), aber mit dem
Eigenwert 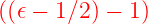 . Der Operator . Der Operator 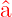 erniedrigt
den Eigenwert um 1. Er wird Absteigeoperator oder
Vernichtungsoperator genannt. erniedrigt
den Eigenwert um 1. Er wird Absteigeoperator oder
Vernichtungsoperator genannt. |
Multiplizieren wir Gleichung (5.17) von links mit 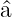 † und
verwenden Gleichung (5.14) erhalten wir
† und
verwenden Gleichung (5.14) erhalten wir
Wenn ϕ(u) eine Lösung der Gleichung (5.17)
mit dem Eigenwert (𝜖 − 1∕2) ist, ist 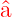 †ϕ(u) eine
Lösung der gleichen Gleichung (5.17), aber mit dem
Eigenwert †ϕ(u) eine
Lösung der gleichen Gleichung (5.17), aber mit dem
Eigenwert 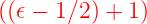 . Der Operator . Der Operator 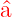 † erhöht den
Eigenwert um 1. Er wird Aufsteigeoperator oder
Erzeugungsoperator genannt. † erhöht den
Eigenwert um 1. Er wird Aufsteigeoperator oder
Erzeugungsoperator genannt. |
Wenn wir eine endliche Energieskala haben, muss es eine
kleinste Energie und damit auch einen kleinsten Eigenwert
geben. Das heisst, es muss eine Ortswellenfunktion ϕ0(u)
geben, auf die angewandt der Vernichtungsoperator 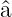 eine
Nullfunktion ergibt.
eine
Nullfunktion ergibt.
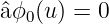 | (5.20) |
Wir verwenden die Definition von 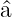 und erhalten
und erhalten
Die Konstante C ergibt sich aus der Normalisierungsbedingung
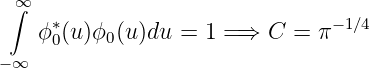 |
Die normierte Wellenfunktion des Grundzustandes des harmonischen Oszillators in den Koordinaten u und x ist
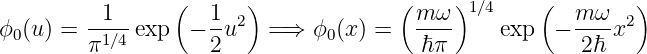 | (5.22) |
Ausgehend von ϕ0(u) können wir nun durch die wiederholte
Anwendung von 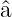 † auf ϕ
0(u) alle Lösungen generieren.
† auf ϕ
0(u) alle Lösungen generieren.
Die ersten nicht normierten Funktionen sind
Mit der Normalisierungsbedingung, dass das Integral über der Wahrscheinlichkeitsdichte gleich eins sein soll, bekommen wir
Aus 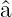 ϕ0(u) = 0 und Gleichung (5.17) folgt, dass
ϕ0(u) = 0 und Gleichung (5.17) folgt, dass
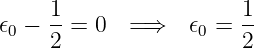 | (5.25) |
Allgemein ist also
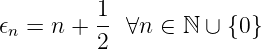 | (5.26) |
Wir erinnern uns an die Substitutionen in Gleichung (5.5). Deshalb sind die
Energieeigenwerte des harmonischen Oszillators
|
Die gleichabständigen Energieeigenwerte des harmonischen Oszillators sind für diesen charakteristisch. Der kleinste Energieeigenwert E0 hat den Wert ℏω∕2. Es ist nicht möglich, einen harmonischen Oszillator in Ruhe zu haben. Die minimale Energie E0 ist die Nullpunktsenergie. Sie bewirkt, dass harmonische Oszillatoren immer Energie enthalten, egal wie tief die Temperatur sinkt. Das heisst, die Boltzmannverteilung aus der klassischen Thermodynamik gilt nicht mehr.
Die Lösungen von Gleichung (5.17) können mit Hermite-Polynomen ausgedrückt werden.[CH67, p. 77, Kap. 2, §9, 4.]
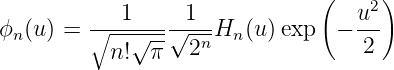 | (5.28) |
mit
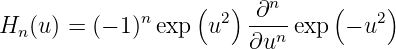 | (5.29) |
Die ersten (nicht normierbaren) Hermite-Polynome sind
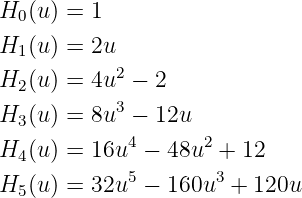 | (5.30) |
Die Normierungsbedingung ist erfüllt, da
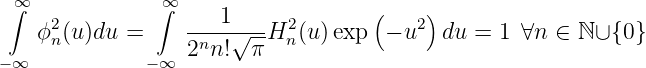 |
ist. Hermite-Polynome haben die folgenden Eigenschaften
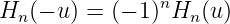 | (5.31) |
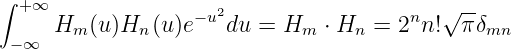 | (5.32) |
__________________________________________________________________________
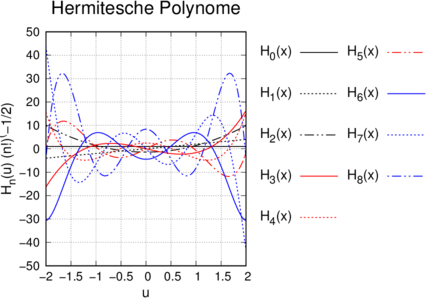
Die ersten acht Hermite-Polynome.
_____________________________________________________________________
Wenn wir die Substitutionen aus Gleichung (5.5) rückgängig machen, erhalten wir aus Gleichung (5.24)
Die Normierungsbedingung ist
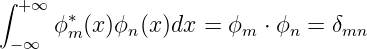 | (5.35) |
__________________________________________________________________________
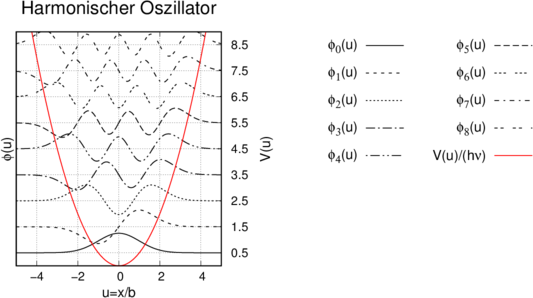
Wellenfunktionen des harmonischen Oszillators
_____________________________________________________________________
_____________________________________________________________________
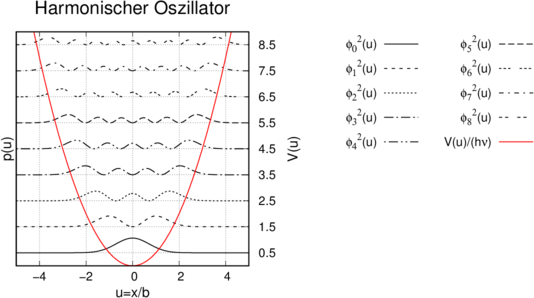
Wahrscheinlichkeitsdichte der Wellenfunktionen des harmonischen Oszillators
_____________________________________________________________________
In diesem Abschnitt soll der quantenmechanische harmonische Oszillator mit dem klassischen Grenzfall verglichen werden. Zuerst soll die Aufenthaltswahrscheinlichkeit als Funktion des Ortes x für einen klassischen Oszillator
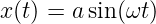 | (5.36) |
und der Amplitude a verglichen werden. Je schneller sich der Oszillator bewegt, desto weniger wahrscheinlich ist sein Aufenthalt am Orte x. Die Geschwindigkeit ist dann
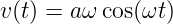 | (5.37) |
Mit der obigen Argumentation ist die Aufenthaltswahrscheinlichkeit proportional zum Kehrwert der Geschwindigkeit, also
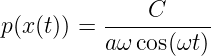 | (5.38) |
Aus dem Ort bekommen wir die Zeit
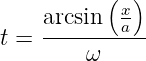 | (5.39) |
Eingesetzt in Gleichung (5.38) bekommen wir
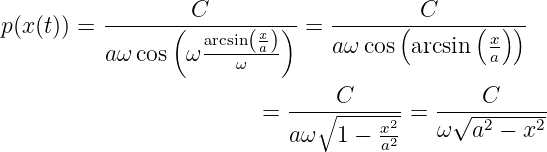 | (5.40) |
Die Konstante C ergibt sich aus der Normierierungsbedingung
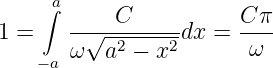 | (5.41) |
Damit ist die klassische Wahrscheinlichkeitsdichte des klassischen harmonischen Oszillators
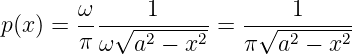 | (5.42) |
Die klassische Wahscheinlichkeitsdichte divergiert an den Grenzen ±a. Dies ist ein Hinweis, dass die klassische Physik vielleicht doch nicht der Weisheit letzter Schluss ist.
Wir vergleichen nun die klassische Wahrscheinlichkeitsdichte mit der quantenmechanischen Wahrscheinlichkeitsdichte.
__________________________________________________________________________
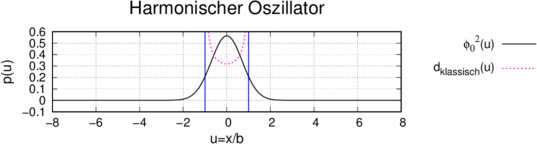
Wahrscheinlichkeitsdichten. Die durchgezogene Linie ist
die Aufenthaltswahrscheinlichkeitsdichte des
harmonischen Oszillators für 𝜖0 = 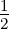 oder E0 =
oder E0 = 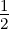 ℏω.
ℏω.
_____________________________________________________________________
Bei Abbildung 5.10.3 ist klar ersichtlich, dass die klassische Wahrscheinlichkeitsdichteverteilung und die quantenmechanische nicht übereinstimmen. Die beiden blauen Linien markieren die Grenze des klassischen harmonischen Oszillators bei dem Energieeigenwert der Wellenfunktion.
__________________________________________________________________________
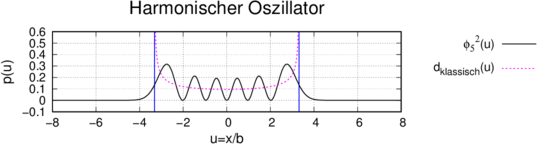
Wahrscheinlichkeitsdichten. Die durchgezogene Linie ist
die Aufenthaltswahrscheinlichkeitsdichte des
harmonischen Oszillators für 𝜖5 = 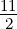 oder E5 =
oder E5 = 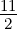 ℏω.
ℏω.
_____________________________________________________________________
Bei Abbildung 5.10.3 ist schon andeutungsweise zu sehen, dass die Aufenthaltswahrscheinlichkeit am Rande des Klassischen harmonischen Oszillators steigt.
__________________________________________________________________________
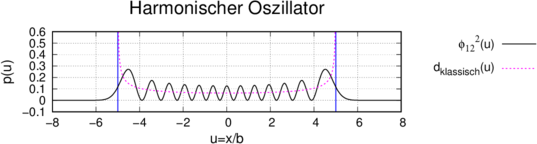
Wahrscheinlichkeitsdichten. Die durchgezogene Linie ist
die Aufenthaltswahrscheinlichkeitsdichte des
harmonischen Oszillators für 𝜖12 = 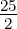 oder E12 =
oder E12 = 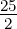 ℏω.
ℏω.
_____________________________________________________________________
Bei den Abbildungen 5.10.3 und 5.10.3 wird mit zunehmender Quantenzahl oder zunehmendem Energiniveau die Ähnlichkeit mit der klassischen Wahrscheinlichkeitsdichteverteilung immer grösser.
__________________________________________________________________________

Wahrscheinlichkeitsdichten. Die durchgezogene Linie ist
die Aufenthaltswahrscheinlichkeitsdichte des
harmonischen Oszillators für 𝜖25 = 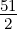 oder E12 =
oder E12 = 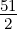 ℏω.
ℏω.
_____________________________________________________________________
Die quantenmechanische Wahrscheinlichkeitsdichte liegt periodisch über und unter der klassischen Dischte. Je grösser n wird, desto mehr Oszillationen gibt es und desto besser würde eine räumliche Mittelung der quantenmechanischen Wahrscheinlichkeitsdichte die klassische Wahrscheinlichkeitsdichte approximieren. Aber egal wie hoch die Quantenzahl n ist, der exponentielle Abfall wird immer da sein. Seine Breite wird mit zunehmender Quantenzahl n relativ kleiner. Ein verwandtes Phänomen ist das Gibbs’sche Phänomen (Überschwingen) bei Rechteckpulsen. Da die reale Fourierreihe immer endlich ist, bleibt das überschwingen.
| Je höher bei quantenmechanischen Systemen die Energiequantenzahl n ist, desto besser wird das klassische System approximiert. |
Ein bekanntes Beispiel für quasi-klassisches Verhalten sind die Rydbergzustände in Atomen.