Weiter: Elektromagnetische Wellen im Doppelleitersystem Oben: Elektromagnetische Wellen Zurück: Elektromagnetische Wellen Skript: PDF-Datei Übungen: Blätter
Im Vakuum gibt es keine Teilchen, also auch keine geladenen Teilchen. Wir können also setzen:
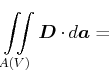 |
(6.512) | ||
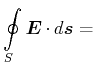 |
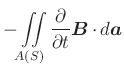 |
||
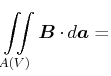 |
|||
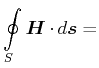 |
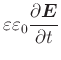 |
| (6.513) | |||
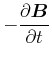 |
|||
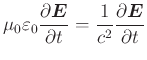 und erhalten also
und erhalten also
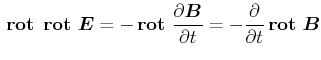 |
(6.515) |
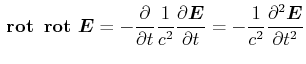 |
(6.516) |
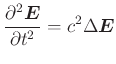 |
(6.517) |
sowie nach einer analogen Ableitung für ![]()
Die nicht-trivialen Lösungen der Wellengleichungen heissen elektromagnetische
Wellen. Dieses Phänomen ist implizit in den Maxwellgleichungen enthalten, die aus makroskopischen Experimenten
abgeleitet wurden. Die Wellengleichung beschreibt alle Wellenphänomene aus der Kommunikationstechnik, der
Optik und der Wechselwirkung von Atomen und Molekülen untereinander, für Abstände von ![]() oder mehr.
Die Maxwellgleichungen sind invariant unter der Lorentz-Transformation, nicht aber unter der
Galilei-Transformation. In jedem Inertialsystem im Vakuum ist die Ausbreitungsgeschwindigkeit
oder mehr.
Die Maxwellgleichungen sind invariant unter der Lorentz-Transformation, nicht aber unter der
Galilei-Transformation. In jedem Inertialsystem im Vakuum ist die Ausbreitungsgeschwindigkeit
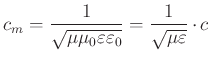 |
(6.520) |
In Medien ist die Ausbreitungsgeschwindigkeit entsprechend
| (6.521) |
Othmar Marti