Weiter: Übungsblätter, Testfragen, Folien und Oben: Berechnung elektrischer Felder Zurück: Innerhalb und ausserhalb einer Skript: PDF-Datei Übungen: Blätter
Nach Abschnitt D.3 ist
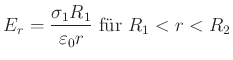 wenn die Ladungsdichte
wenn die Ladungsdichte ![]() auf der
Zylinderschale mit
auf der
Zylinderschale mit ![]() aufgebracht ist. Wir betrachten zwei konzentrische Zylinder mit den Radien
aufgebracht ist. Wir betrachten zwei konzentrische Zylinder mit den Radien ![]() und deren Oberflächenladungsdichten
und deren Oberflächenladungsdichten ![]() und
und ![]() . Für
. Für ![]() gilt
gilt
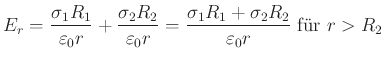

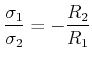
![\includegraphics[width=0.8\textwidth]{koaxladung}](img2258.gif)
Elektrische Felder bei einem Koaxialkabel, wobei einmal (dünne Linie) die Oberflächenladungsdichten
|
Othmar Marti