Weiter: Magnetische Eigenschaften der Materie Oben: Zeitlich veränderliche Magnetfelder Zurück: Das Faradaysche Induktionsgesetz Skript: PDF-Datei Übungen: Blätter
![\includegraphics[width=0.6\textwidth]{magnetismus-018}](img1395.gif)
Berechnung der Energie im Magnetfeld
|
Wir betrachten eine mit einer Wechselstromquelle
![]() verbundene reale Spule. Diese Spule
wird modelliert durch einen Widerstand
verbundene reale Spule. Diese Spule
wird modelliert durch einen Widerstand ![]() und eine ideale Spule
und eine ideale Spule ![]() . Die Differentialgleichung dieses Kreises
lautet
. Die Differentialgleichung dieses Kreises
lautet
| (4.434) |
| (4.435) |
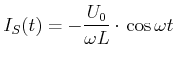 |
(4.436) |
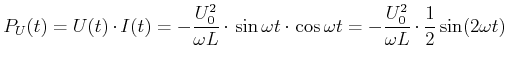 |
(4.437) |
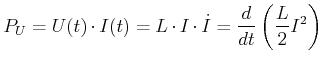 |
(4.438) |
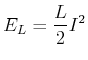 |
(4.439) |
| (4.440) |
| (4.441) |
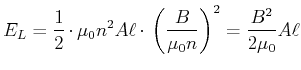 |
(4.442) |
Othmar Marti