Poynting-Vektor und Energiefluss

Berechnung des Poynting-Vektors

Wir hatten gesehen, dass das elektrische wie das magnetische Feld eine Energiedichte haben. Da sich bei Wellen diese Felder mit der Geschwindigkeit $c$ ausbreiten, muss es einen Energiefluss geben. Wir betrachten einen Rechteckpuls auf einem Zweileitersystem. Der Energiefluss durch eine raumfeste Fläche $A=b\cdot d$ bezeichnen wir mit $S_z$, dem Energiefluss pro Flächen- und Zeiteinheit. Die in der Zeit $dt$ transportierte Energie ist

$$S_z\cdot A\cdot dt = \left(\frac{\varepsilon_0}{2}E_x^2+\frac{1}{2\mu_0}B_y^2\right)\cdot A \cdot dt \cdot c$$ (6.547)

Für beliebige fortlaufende Wellen im Vakuum gilt

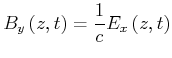$$B_y\left(z\text{,} t\right) = \frac{1}{c}E_x\left(z\text{,} t\right)$$ (6.548)

Wir können damit die Gleichung (6.30) symmetrisch schreiben

$$S_z = \left(\frac{\varepsilon_0 \cdot c}{2}E_x\cdot B_y +\frac{1}{2\mu_0\cdot c}E_x\cdot B_y\right)\cdot c$$

$$= \frac{1}{2\mu_0} E_x \cdot B_y+\frac{1}{2\mu_0} E_x \cdot B_y$$

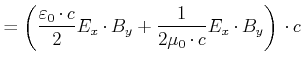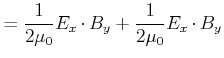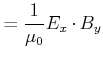$$=\frac{1}{\mu_0} E_x \cdot B_y$$ (6.549)

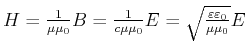Mit $H = \frac{1}{\mu\mu_0}B= \frac{1}{c\mu\mu_0}E=\sqrt{\frac{\varepsilon\varepsilon_0}{\mu\mu_0}}E$ bekommen wir

$$S = \sqrt{\frac{\varepsilon\varepsilon_0}{\mu\mu_0}} E^2$$ (6.550)

Damit ist auch klar, dass das $\vec{E}$-Feld und das $\vec{B}$-Feld je zur Hälfte zum Energiefluss beitragen.

Die allgemeine Form des Energieflusses im Vakuum ist

$$\vec{S}\left(\vec{r}\text{,} t\right) = \frac{1}{\mu_0} \vec{E}\left(\vec{r}\text{,} t\right)\times \vec{B}\left(\vec{r}\text{,} t\right)$$ (6.551)

In Medien muss der Energiefluss wie

$$\vec{S}\left(\vec{r}\text{,} t\right) = \vec{E}\left(\vec{r}\text{,} t\right)\times \vec{H}\left(\vec{r}\text{,} t\right)$$ (6.552)

geschrieben werden. $\left\vert\vec{S}\right\vert$ gibt die in Richtung $\vec{S}$ fliessende Energie pro Flächeneinheit und Zeit wieder. Die Einheit von $S$ ist $J/(m^2\cdot s)$. Da $\vec{H}$ und $\vec{B}$ über einen Tensor verbunden sein können, muss der Energiefluss nicht unbedingt in die Richtung des Wellenvektors zeigen. Dieses Verhalten ist die Grundlage von optisch doppelbrechenden Materialien.