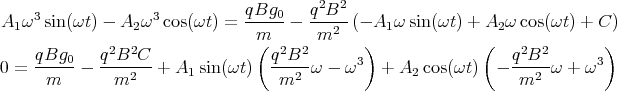1 Punkt
Die neue Kapazität ist
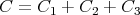
1 Punkt
Also ist
U = 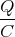 | = 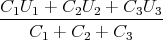 | ||
= 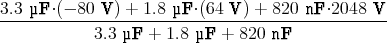 = 258.5 V = 258.5 V |
∑ 3 Punkte
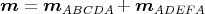
1 Punkt
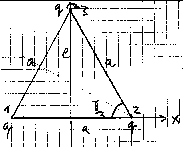
Wir setzen a = BC = 50 mm, b = AB = 18 mm und c = AF = 15 mm. Wir bekommen

1 Punkt
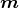 liegt in der yz-Ebene.
liegt in der yz-Ebene. 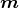 ABCDA zeigt in die -z-Richtung,
ABCDA zeigt in die -z-Richtung, 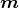 ADEFA in die +y-Richtung.
ADEFA in die +y-Richtung.
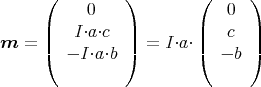
1 Punkt
Eingesetzt bekommt man
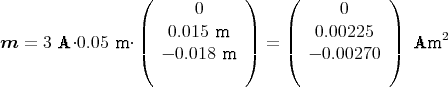
1 Punkt
∑ 4 Punkte
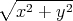 und lassen den Strom I entlang der z-Achse fliessen. Wir wollen
zeigen, dass
und lassen den Strom I entlang der z-Achse fliessen. Wir wollen
zeigen, dass
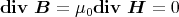
ist. Das Magnetfeld ist tangential, der Einheitsvektor, der in Richtung des Magnetfeldes zeigt, sei
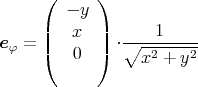
1 Punkt
div 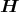 | = div 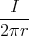  φ φ | |||||||||
= div 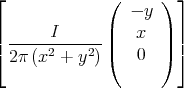 | 1 Punkt | |||||||||
= 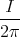 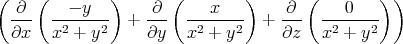 | 1 Punkt | |||||||||
= 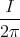 ![[ ( - y⋅2x ) ( x⋅2y ) ]
- ---------2 + - ---------2
(x2 + y2) (x2 + y2)](klausur-el-2009454x.png) | 1 Punkt | |||||||||
= 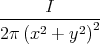 ![[2yx - 2xy ]](klausur-el-2009456x.png) | = | 0 | 1 Punkt | |||||||
∑ 5 Punkte
- Alle drei Ladungen sind äquivalent. Die Ladungen 1 und 2 erzeugen eine Kraft auf
die Ladung drei in Richtung der +z-Achse.
Mit den gegebenen Werten:
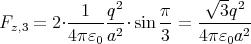
1 Punkt
da der Abstand von 1 und 3 vektoriell geschrieben
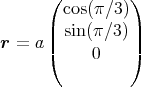
ist.
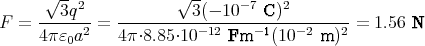
1 Punkt
F zeigt weg von der Mitte des Dreiecks.
1 Punkt
- Die Mitte des gleichseitigen Dreiecks teilt die Winkelhalbierende im Verhältnis
1:2.
Länge der Winkelhalbierenden: ℓw =
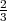 ℓ =
ℓ = 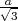 .
.
Kräftefrei heisst:
F + F0 = 0 F0 = 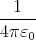
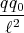
= - 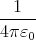
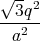
1 Punkt 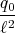
= - 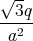
q0 = - 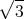 q
q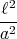
= - 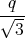
1 Punkt q0 = - 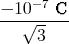
= 57.735 nC 1 Punkt
∑ 6 Punkte
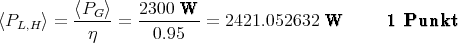
erforderlich. Der Strom durch die Leitung ist
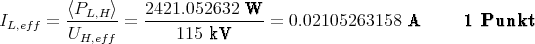
Der Widerstand einer Leitung ist
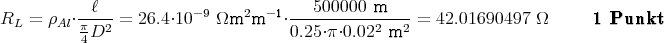
Der Gesamtwiderstand ist 2RL. Dies führt zu einem Spannungsabfall in der Leitung von
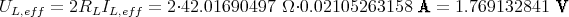
Auf der Hochspannungsseite des Transformators beim Kraftwerk brauchen wir eine Spannung von
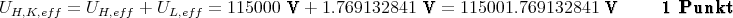
Die Leistung ist dann
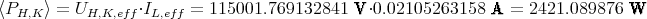
- Primärseitig ist die Leistung am Kraftwerk
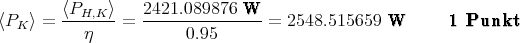
- Der Strom ist
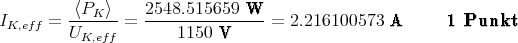
∑ 6 Punkte
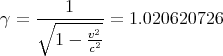
Die Lorentztransformation für die Felder lautet dann
| Ex′ | = Ex | ||
| Ey′ | = γ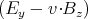 | ||
| Ez′ | = γ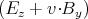 | ||
| Bx′ | = Bx | ||
| By′ | = γ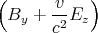 | ||
| Bz′ | = γ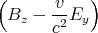 | ||
Das elektrische Feld bei  =
= 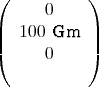 ist
ist
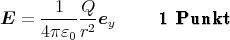
Es hat also eine y-Komponente. Alle anderen Felder sind null. Im Ruhesystem des Raumschiffes ist dann mit
| Ex′ | = 0 | |||||||||
| Ey′ | = γ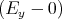 | = | 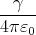 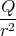 | 1 Punkt | ||||||
| Ez′ | = γ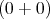 | |||||||||
| Bx′ | = 0 | |||||||||
| By′ | = γ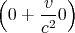 | |||||||||
| Bz′ | = γ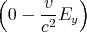 | = | -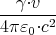 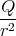 | 1 Punkt | ||||||
Mit den Zahlenwerten bekommen wir
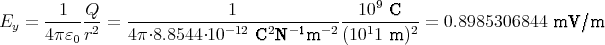
(1 Punkt) und
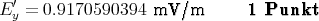
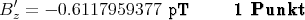
Mit Taschenrechner berechnet gibt es grössere Rundungsfehler!
∑ 6 Punkte
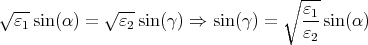
und
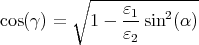
| Ir | = Ie![[sinγ(α )cosα - sin α cosγ(α )]2
------------------------------2
[sinγ(α )cosα + sin α cosγ(α )]](klausur-el-2009502x.png) | ||||||
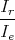 | = lim α→0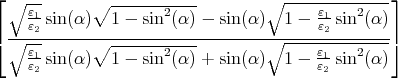 2 2
| 1 Punkt | |||||
= lim α→0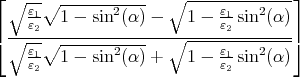 2 2
| |||||||
= 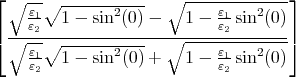 2 2
| |||||||
= 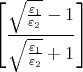 2 2 | = | ![[√ -- √ --]
√-ε1 --√-ε2
ε1 + ε2](klausur-el-2009508x.png) 2 2 | |||||
| 1 Punkt | |||||||
| 1. Material | Wasser | InSb | Diamant | Luft | |
| 2. Material | ε | 81 | 15.7 | 5.7 | 1 |
| Wasser | 81 | - | 0.151 | 0.337 | 0.640 |
| InSb | 15.7 | 0.151 | - | 0.0615 | 0.356 |
| Diamant | 5.7 | 0.337 | 0.0615 | - | 0.168 |
| Luft | 1 | 0.640 | 0.356 | 0.168 | - |
6 Punkte
∑ 8 Punkte
Bei einem bestimmten Strom addieren sich die die Diodenspannungen.
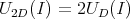
Wir zeichnen diese neue Kurve zusammen mit der rückwärts gezeichneten Widerstandskurve für verschiedene Spannungen auf:
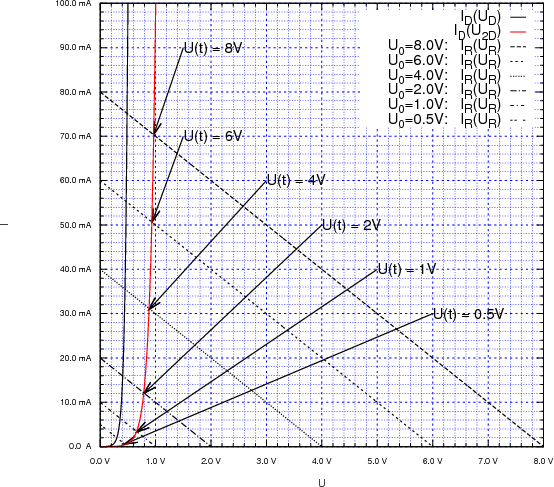
3 Punkte
Aus den Schnittpunkten lesen wir die folgenden Werte ab und verwenden
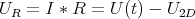
| U(t)[V] | U2D[V] | I[A] | UR[V] |
| -8 | 0.967 | 0.0704 | 7.04 |
| -6 | 0.940 | 0.0507 | 5.07 |
| -4 | 0.881 | 0.0309 | 3.09 |
| -2 | 0.788 | 0.0120 | 1.20 |
| -1 | 0.659 | 0.0033 | 0.33 |
| -0.5 | 0.363 | 0.0006 | 0.06 |
| 0 | 0 | 0 | 0 |
| 0.5 | 0.363 | 0.0006 | 0.06 |
| 1 | 0.659 | 0.0033 | 0.33 |
| 2 | 0.788 | 0.0120 | 1.20 |
| 4 | 0.881 | 0.0309 | 3.09 |
| 6 | 0.940 | 0.0507 | 5.07 |
| 8 | 0.967 | 0.0704 | 7.04 |
4 Punkte für die Werte grösser oder kleiner Null
1 Punkt für Werte mit beiden Vorzeichen
∑ 8 Punkte
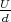 (U = Spannung an den Elektroden, d =
Elektrodenabstand), der Elektrodenfläche A, der Beweglichkeit μj und der Ionenladung
qj
(U = Spannung an den Elektroden, d =
Elektrodenabstand), der Elektrodenfläche A, der Beweglichkeit μj und der Ionenladung
qj
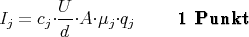
Die Ladungsdichte cj⋅qj infolge des Ions j ergibt sich aus dem Gewichtsanteil ai der Lösung i an der Gesamtmenge, dem Gewichtsanteil bij des Ions j in der Lösung i, dem Molekulargewicht des Ions mj und der Dichte der Lösung ρ zu
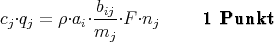
wobei nj die Zahl der Elementarladungen e0 des Ions ist und F die Faraday-Konstante. Zusammen ergibt sich damit für den Anteil des Ions j:
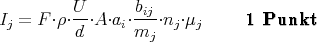
Der Gesamtstrom ergibt sich aus der Summation über alle Ionen:
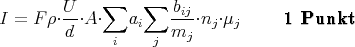
Für die Anionen (hier CN-) hat n j ein negatives Vorzeichen, aber die Beweglichkeit ist in diesem Fall ebenfalls negativ, so dass hier mit den Beträgen gerechnet werden kann.
Durch Einsetzen und Aufsummieren aller Grössen ergibt sich
| I = | 9.65⋅104 Cmol-1⋅1300 kgm-3⋅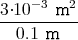 | |||||
⋅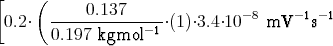 | ||||||
+ 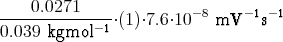 | ||||||
+ 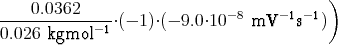 | ||||||
+ 0.8⋅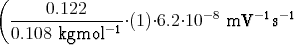 | ||||||
+ 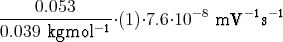 | ||||||
+ 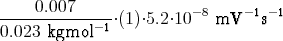 | ||||||
+ ![)]
---0.0726-----⋅(- 1)⋅(- 9.0⋅10-8 mV - 1s- 1)
0.026 kgmol - 1](klausur-el-2009524x.png) | 4 Punkte | |||||
| = | 14.8 A | 1 Punkt |
∑ 9 Punkte
- Die Bewegungsgleichung lautet
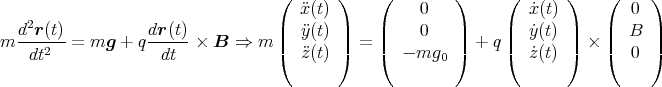
In Komponenten
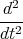 x(t)
x(t)= - 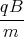
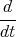 z(t)
z(t)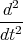 y(t)
y(t)= 0 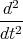 z(t)
z(t)= -g0 + 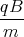
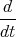 x(t)& 1 Punkt
x(t)& 1 Punkt - Wir differenzieren die erste Gleichung nach t und setzen die dritte Gleichung
ein.
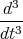 x(t)
x(t)= - 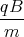
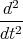 z(t)
z(t)= - 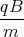
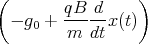
1 Punkt 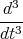 x(t)
x(t)= 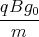 -
-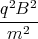
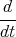 x(t)
x(t)1 Punkt - Wir verwenden den Ansatz x(t) = A1 cos(ωt) + A2 sin(ωt) + Ct und setzen ein
Damit muss
sein. Die Lösung istC = 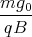
ω = 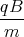
1 Punkt 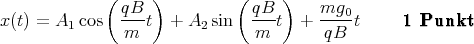
- Wir integrieren die dritte Differentialgleichung einmal und setzen x(t) ein.
ż(t) = -g0t + 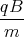 x(t) + D
x(t) + D= -g0t + 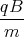
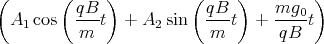 + D
+ D1 Punkt = A1 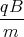 cos
cos 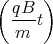 + A2
+ A2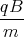 sin
sin 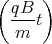 + D
+ Dz(t) = A1 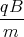
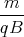 sin
sin 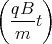 - A2
- A2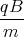
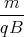 cos
cos 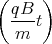 + Dt + E
+ Dt + E= A1 sin 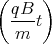 - A2 cos
- A2 cos 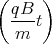 + Dt + E
+ Dt + E1 Punkt - Für t = 0 haben wir
Damit ist die Lösung0 = x(0) = A1 0 = z(0) = - A2 + E 1 Punkt 0 = ẋ(0) = - A1 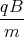 sin
sin 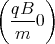 + A2
+ A2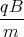 cos
cos 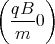 +
+ 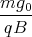
= A2 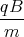 +
+ 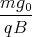
0 = ż(0) = A1 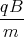 cos
cos 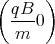 + A2
+ A2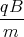 sin
sin 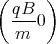 + D
+ D= A1 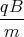 + D
+ D1 Punkt ⇒ A1 = 0 ⇒ D = 0 ⇒ A2 = - 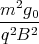
⇒ E = - 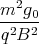
x(t) = - 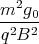 sin
sin 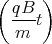 +
+ 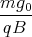 t
t1 Punkt z(t) = 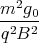 cos
cos 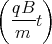 -
-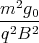
1 Punkt - Die z-Komponente der Bahn ist maximal negativ wenn
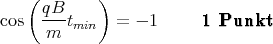
ist. Dann ist
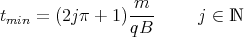
und
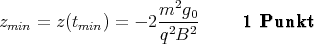
Zur Visualisierung (nicht gefragt in der Klausur) finden Sie hier x(t) und z(t) aufgetragen sowie z(x). Die Werte waren m == 0.0003 kg, g0 = 9.81 ms-2, q = 0.01 C und B = 0.5 T.
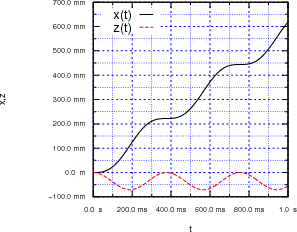
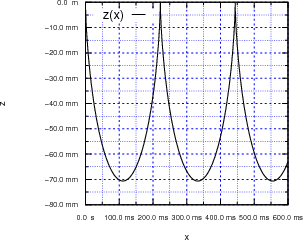
∑ 13 Punkte
- An der Grenzfläche ist die Senkrechtkomponente von
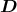 stetig. Hier ist dies wegen
der Kugelsymmetrie D selber.
stetig. Hier ist dies wegen
der Kugelsymmetrie D selber.
1 Punkt
- An der Grenzfläche ist φ(r) stetig.
1 Punkt
- Wir berechnen die Lösung innerhalb der Kugel verwenden die Gleichung
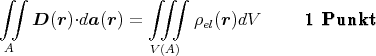
Das gestellte Problem ist kugelsymmetrisch, also muss auch die Lösung kugelsymmetrisch sein. Wir setzen A als Kugelschale mit dem Zentrum der geladenen Kugel im Zentrum der Kugelschale.
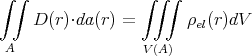
Das erste Integral ergibt (da D(r) über der ganzen Kugeloberfläche konstant ist)
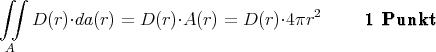
Das zweite Integral ergibt
Damit bekommen wir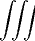 V (A) ρel(r)dV
V (A) ρel(r)dV = ∫ 0r ∫ 02π ∫ 0πρ 0 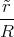 sin θdθdϕ
sin θdθdϕ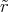 2d
2d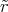
= 4π 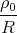 ∫
0π
∫
0π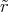
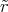 2d
2d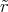
= 4π 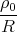
![[ 4]
r˜
4](klausur-el-2009599x.png) 0r
0r= 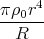 1 Punkt
1 Punkt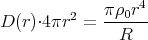
oder
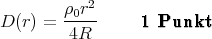
Vektoriell geschrieben bekommen wir
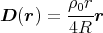
Am Rande der Kugel ist die dielektrische Verschiebung
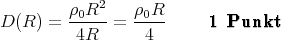
Ausserhalb der Kugel gilt das Coulombsche Gesetz (die Senkrechtkomponente von D ist kontinuierlich)
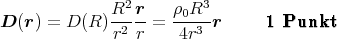
Zusammen
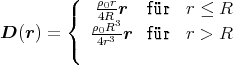
- Das elektrostatische Potential ist (Kugelsymmetrie)
An der Grenze der Ladungsverteilung istφ(r) = -∫ ∞r 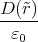 d
d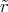
= -∫ ∞r 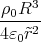 d
d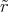
= - 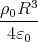 ∫
∞r
∫
∞r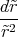
= - 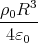
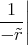 ∞r
∞r= 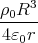 1 Punkt
1 Punkt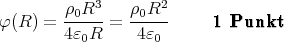
Innerhalb der Kugel erhalten wir
Zusammenφ(r) - φ(R) = -∫ Rr 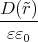 d
d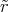
= - 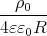 ∫
Rr
∫
Rr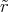 2d
2d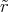
= - 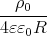
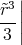 Rr = -
Rr = -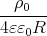
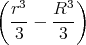 =
= 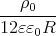
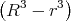
1 Punkt φ(r) = 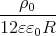
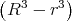 + φ(R)
+ φ(R)= 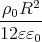 -
-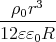 +
+ 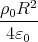
= 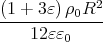 -
-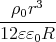
1 Punkt 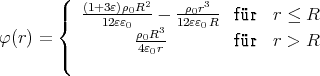
- Am Zentrum der Ladungsverteilung ist
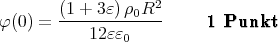
∑ 13 Punkte