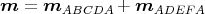
2 Punkte
Wir setzen a = BC = 50 mm, b = AB = 18 mm und c = AF = 15 mm. Wir bekommen

1 Punkt
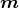 liegt in der yz-Ebene.
liegt in der yz-Ebene. 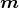 ABCDA zeigt in die -z-Richtung,
ABCDA zeigt in die -z-Richtung, 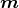 ADEFA in die +y-Richtung.
ADEFA in die +y-Richtung.

1 Punkt
Eingesetzt bekommt man
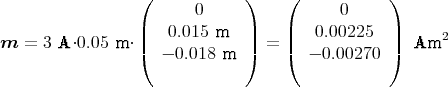
1 Punkt
∑ 5 Punkte
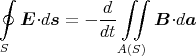
1 Punkt
Mit dem Abstand r = 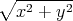 bekommen wir
bekommen wir
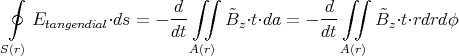
3 Punkte
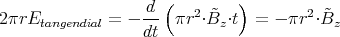
1 Punkt
und damit
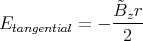
1 Punkt
∑ 6 Punkte
- Der Poyntingvektor der Sonnenstrahlung in Erdentfernung R zur Sonne ist - mit
PS = 3.82⋅1020 MW Strahlungsleistung der Sonne -
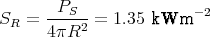
1 Punkt
- Daraus ergeben sich die mittleren (effektiven) Feldstärken zu
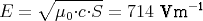
1 Punkt
bzw.
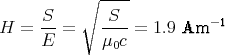
1 Punkt
- Am Frühjahrsanfang (und Herbstanfang) ist die Schrägstellung der Erdachse nicht
zu berücksichtigen. Zum lokalen Mittag, der bei Frühjahrsanfang in Ulm 12 : 20
Uhr MEZ ist (MEZ
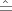 15° östliche Länge, 5° Differenz
15° östliche Länge, 5° Differenz 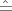 20 min), ist dann, unter
Beachtung der geographischen Breite φ = 48.4°, die einfallende Sonneneinstrahlung
20 min), ist dann, unter
Beachtung der geographischen Breite φ = 48.4°, die einfallende Sonneneinstrahlung
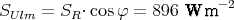
2 Punkte
∑ 5 Punkte
- DLuft = DParaffin
ELuft = 2EParaffin
1 Punkt
-
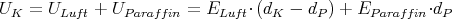
Mit der ersten Teilaufgabe
![U [2(d - d ) + d ]⋅E
K K P P Paraffin](nachklausur-el-200966x.png)
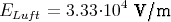
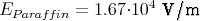
2 Punkte
-
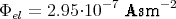
1 Punkt
-
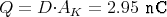
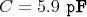
1 Punkt
-
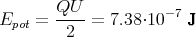
1 Punkt
-
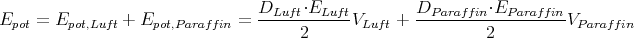
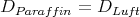
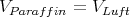
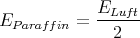
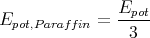
2 Punkte
∑ 8 Punkte
- Wir berechnen zunächst den durch den Stab fliessenden Strom. Die Spannungsquelle
liefert eine Spannung U, und der Stab induziert aufgrund seiner Bewegung eine
Gegenspannung mit dem Betrag Bℓv. Also ist die resultierende Spannung U-Bℓv =
IR. Daraus folgt I =
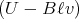 ∕R. Wegen dieses Stromes im Stab wirkt auf ihn
durch das magnetische Feld die Kraft F = IℓB =
∕R. Wegen dieses Stromes im Stab wirkt auf ihn
durch das magnetische Feld die Kraft F = IℓB = 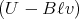 Bℓ∕R = ma.
Bℓ∕R = ma.
2 Punkte
- Die Endgeschwindigkeit ve tritt auf, wenn F = 0 ist, also wenn gilt U - Bℓve = 0.
Daraus folgt ve = U∕
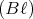 .
.
2 Punkte
- Bei der Endgeschwindigkeit ist der Strom im Stab I =
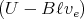 ∕R = 0.
∕R = 0.
2 Punkte
∑ 6 Punkte
- Wir verwenden die Lorentztransformation aus der Formelsammlung
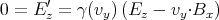
Die Geschwindigkeit muss in die y-Richtung zeigen.
1 Punkt
Daraus erhalten wir
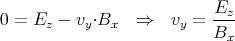
1 Punkt
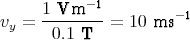
1 Punkt
- Die Felder sind gleich wie vorher, aber Bx soll im bewegten Bezugssystem null sein.
Also muss
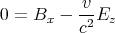
sein.
1 Punkt
Die Geschwindigkeit ist dann in die y-Richtung und hat den Betrag
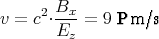
1 Punkt
- Die Teilaufgabe a) ist physikalisch sinnvoll, die Teilaufgabe b) nicht (da dann vy > c
ist.)
1 Punkt
∑ 6 Punkte
Bei einem bestimmten Strom addieren sich die die Diodenspannungen.
Wir zeichnen diese neue Kurve zusammen mit der rückwärts gezeichneten Widerstandskurve für verschiedene Spannungen auf:
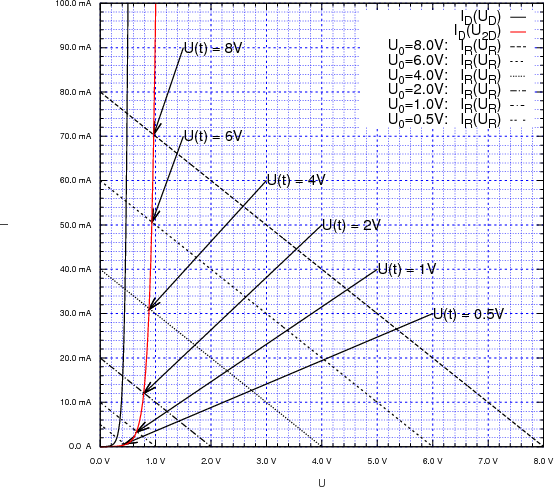
4 Punkte
Aus den Schnittpunkten lesen wir die folgenden Werte ab und verwenden
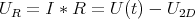
| U(t)[V] | U2D[V] | I[A] | UR[V] |
| -8 | 0.967 | 0.0704 | 7.04 |
| -6 | 0.940 | 0.0507 | 5.07 |
| -4 | 0.881 | 0.0309 | 3.09 |
| -2 | 0.788 | 0.0120 | 1.20 |
| -1 | 0.659 | 0.0033 | 0.33 |
| -0.5 | 0.363 | 0.0006 | 0.06 |
| 0 | 0 | 0 | 0 |
| 0.5 | 0.363 | 0.0006 | 0.06 |
| 1 | 0.659 | 0.0033 | 0.33 |
| 2 | 0.788 | 0.0120 | 1.20 |
| 4 | 0.881 | 0.0309 | 3.09 |
| 6 | 0.940 | 0.0507 | 5.07 |
| 8 | 0.967 | 0.0704 | 7.04 |
4 Punkte für die Werte grösser oder kleiner Null
1 Punkt für Werte mit beiden Vorzeichen
∑ 9 Punkte
- Mit B = μμ0H und μ = 1 + χm bekommt man
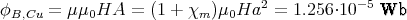
3 Punkte
- Der Fluss im Streufeld ist
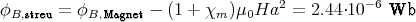
3 Punkte
∑ 6 Punkte
- Die Bewegungsgleichung lautet
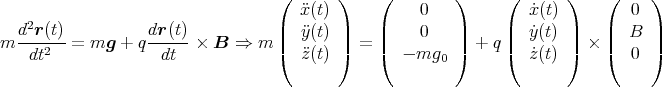
In Komponenten
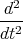 x(t)
x(t)= - 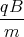
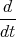 z(t)
z(t)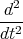 y(t)
y(t)= 0 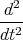 z(t)
z(t)= -g0 + 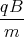
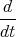 x(t) 2 Punkte
x(t) 2 Punkte - Wir differenzieren die erste Gleichung nach t und setzen die dritte Gleichung
ein.
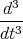 x(t)
x(t)= - 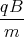
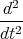 z(t)
z(t)= - 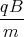
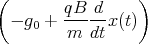
1 Punkt 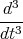 x(t)
x(t)= 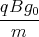 -
-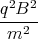
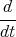 x(t)
x(t)1 Punkt - Wir verwenden den Ansatz x(t) = A1 cos(ωt) + A2 sin(ωt) + Ct und setzen ein
Damit muss
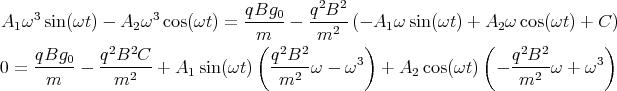
sein. Die Lösung istC = 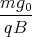
ω = 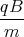
1 Punkt 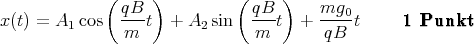
- Wir integrieren die dritte Differentialgleichung einmal und setzen x(t) ein.
ż(t) = -g0t + 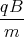 x(t) + D
x(t) + D= -g0t + 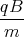
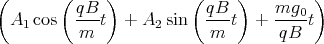 + D
+ D1 Punkt = A1 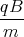 cos
cos 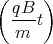 + A2
+ A2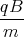 sin
sin 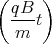 + D
+ Dz(t) = A1 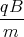
 sin
sin 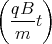 - A2
- A2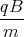
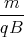 cos
cos 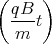 + Dt + E
+ Dt + E= A1 sin 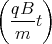 - A2 cos
- A2 cos 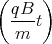 + Dt + E
+ Dt + E1 Punkt - Für t = 0 haben wir
Damit ist die Lösung0 = x(0) = A1 0 = z(0) = - A2 + E 1 Punkt 0 = ẋ(0) = - A1 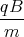 sin
sin 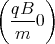 + A2
+ A2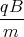 cos
cos 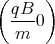 +
+ 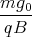
= A2 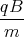 +
+ 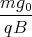
0 = ż(0) = A1 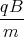 cos
cos 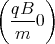 + A2
+ A2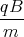 sin
sin 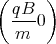 + D
+ D= A1 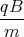 + D
+ D1 Punkt ⇒ A1 = 0 ⇒ D = 0 ⇒ A2 = - 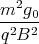
⇒ E = - 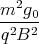
x(t) = - 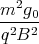 sin
sin 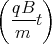 +
+ 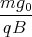 t
t1 Punkt z(t) = 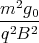 cos
cos 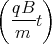 -
-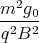
1 Punkt - Die z-Komponente der Bahn ist maximal negativ wenn
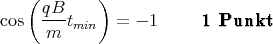
ist. Dann ist
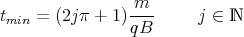
und
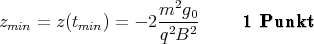
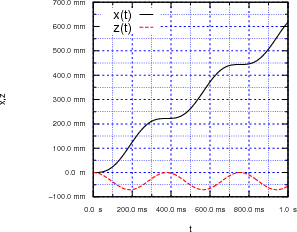
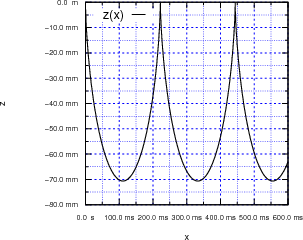
Zur Visualisierung (nicht gefragt in der Nachklausur) finden Sie hier x(t) und z(t) aufgetragen sowie z(x). Die Werte waren m = 0.0003 kg, g0 = 9.81 ms-2, q = 0.01 C und B = 0.5 T.
∑ 14 Punkte
- Die Geschwindigkeit eines Elektrons hat bezüglich dem Magnetfeld zwei Anteile,
deren Grösse von dem eingeschlossenen Winkel α abhängen.
parallel zum Feld: vp = v⋅ cos α
senkrecht zum Feld: vs = v⋅ sin α
2 Punkte
Das Magnetfeld wirkt über die Lorenzkraft
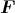 = q
= q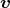 × B auf die Flugbahn des
Elektrons.
× B auf die Flugbahn des
Elektrons.
1 Punkt
Der parallele Anteil wird durch das Feld nicht verändert, es liegt also eine unbeschleunigte gleichförmige Bewegung parallel zum Feld vor.
Der senkrechte Anteil erfährt über die Kraft Fs = qB⋅v sin φ = qB⋅vs eine stetige Richtungsänderung, die zu einer Kreisbahn senkrecht zum Magnetfeld führt.
1 Punkt
Die Zentrifugalkraft m⋅
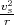 = m⋅ω⋅vs ist nun gleich der Lorenzkraft: mωvs = qB⋅vs
woraus die Kreisfrequenz ω =
= m⋅ω⋅vs ist nun gleich der Lorenzkraft: mωvs = qB⋅vs
woraus die Kreisfrequenz ω = 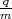 B und die Periodendauer eines Umlaufs
B und die Periodendauer eines Umlaufs
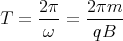
2 Punkte
sich ergibt.
Die Elektronen bewegen sich parallel zum Magnetfeld mit einer konstanten Geschwindigkeit und führen senkrecht dazu eine kreisförmige Bewegung aus, also insgesamt eine schraubenförmige Bahn.
-
Nach der Zeit T treffen sie sich wieder alle in einem Punkt, der
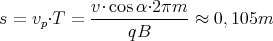
2 Punkte
entfernt ist.
Ein Magnetfeld fokussiert also sich divergent bewegende Ladungen, sofern sie alle die gleiche Geschwindigkeit haben und das gleiche Verhältnis
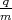 .
.
∑ 8 Punkte
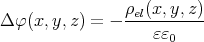
1 Punkt
und setzen die gegebene Gleichung ein. Da x, y und z gleichbedeutend sind, setzen wir a2 = y2 + z2 und leiten nur nach x ab.
| 1 Punkt | 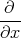 φ0(x,y,z) φ0(x,y,z) | = φ0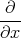 e-(x2+a2)∕r02 e-(x2+a2)∕r02
| |||||
= -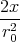 φ0e-(x2+a2)∕r02 φ0e-(x2+a2)∕r02
| |||||||
| 1 Punkt | -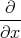 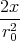 φ0e-(x2+a2)∕r02 φ0e-(x2+a2)∕r02
| = -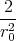 φ0e-(x2+a2)∕r02
+ φ0e-(x2+a2)∕r02
+ 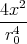 φ0e-(x2+a2)∕r02 φ0e-(x2+a2)∕r02
| |||||
| 1 Punkt | 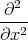 φ0(x,y,z) φ0(x,y,z) | = 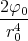 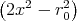 e-(x2+y2+z2)∕r02 e-(x2+y2+z2)∕r02
| |||||
| 1 Punkt | ρel(x,y,z) | = -εε0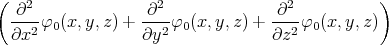 | |||||
| 1 Punkt | = -εε0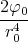 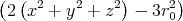 e-(x2+y2+z2)∕r02 e-(x2+y2+z2)∕r02
| ||||||
| 1 Punkt | ρel(r) | = -εε0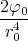 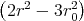 e-r2∕r02 e-r2∕r02
| |||||
∑ 7 Punkte