Weiter: Mittlerer Geschwindigkeitsbetrag der Maxwell-Boltzmann-Verteilung Oben: Rechnen mit Integralen Zurück: Berechnung von Linienintegralen Skript: PDF-Datei Übungen: Blätter
Gesucht ist
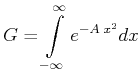 |
Dieses Integral kann in einer Dimension nicht gelöst werden. In zwei
Dimensionen (![]() und
und ![]() ) können wir schreiben (
) können wir schreiben (![]() ist das Integral mit der
Variable
ist das Integral mit der
Variable ![]() geschrieben)
geschrieben)
![$\displaystyle = \left[\int\limits_{-\infty}^\infty e^{-A\;x^2} dx\right]\cdot \left[\int\limits_{-\infty}^\infty e^{-A\;y^2} dy\right]$](img3131.gif) |
||
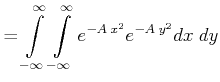 |
||
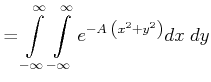 |
Wir schreiben nun
![]() in Zylinderkoordinaten. Aus der
Jacobi-Determinante bekommt man
in Zylinderkoordinaten. Aus der
Jacobi-Determinante bekommt man
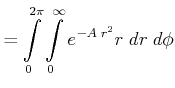 |
||
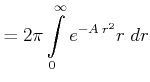 |
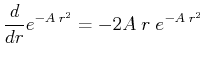 |
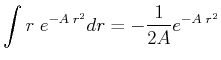 |
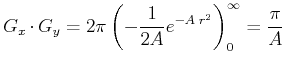 |
Othmar Marti