Weiter: Umrechnungen zwischen Koordinatensystemen Oben: Rechnen mit Integralen Zurück: Berechnung der Fläche unter Skript: PDF-Datei Übungen: Blätter
Wir berechnen
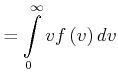 |
||
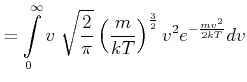 |
||
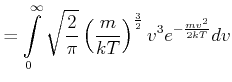 |
||
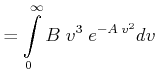 |
mit
![]() und
und
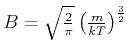 . Zur Lösung machen wir die Substitution
. Zur Lösung machen wir die Substitution
![]() . Dann ist
. Dann ist
![]() . Das Integral wird dann durch partielle
Integration gelöst
. Das Integral wird dann durch partielle
Integration gelöst
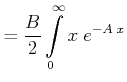 |
||
![$\displaystyle = \frac{B}{2}\left[\left.x\;\frac{1}{-A}\;e^{-A\;x}\right\vert _0^\infty-\frac{1}{-A}\int\limits_0^\infty \;e^{-A\;x} dx\right]$](img3152.gif) |
||
![$\displaystyle =\frac{B}{2}\left[ \left.-\frac{x}{A}\;e^{-A\;x}\right\vert _0^\infty+\left.\frac{1}{A}\frac{1}{-A}e^{-A\;x}\right\vert _0^\infty\right]$](img3153.gif) |
||
![$\displaystyle = \frac{B}{2}\left[0 -\frac{1}{A^2}(-1)\right]$](img3154.gif) |
||
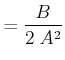 |
Zurück eingesetzt ergibt
Othmar Marti