|
|

| Dieser Stoff wurde am 9. 12. 2004 behandelt |
(Siehe Leisi, Klassische Physik II [Lei98, pp. 71]) (Siehe Tipler, Physik [Tip94, pp. 751])
|
|
Allgemein gilt für einen Leiter, dass
| (3.159) |
|
|
![]() ist die Leitfähigkeit. Ihre Einheit ist
ist die Leitfähigkeit. Ihre Einheit ist
![$\displaystyle \left[ \sigma\right] =\frac{A}{m^{2}} \frac{ m}{ V }
=\frac{A}{Vm}
$](img703.gif)
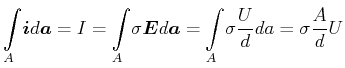 |
(3.161) |
![$\displaystyle \left[ G\right]
=\textrm{Siemens}=\frac{A}{Vm}\frac{m^{2}}{m}=\frac{A}{V}$](img706.gif)
Bekannter ist die Form
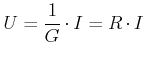 |
(3.163) |
![$\displaystyle \left[ R\right]
=\Omega=\frac{1}{S}=\frac{V}{A}=\frac{W}{A^{2}}$](img709.gif)
Die zu ![]() gehörende mikroskopische Grösse ist der spezifische Widerstand
gehörende mikroskopische Grösse ist der spezifische Widerstand
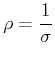 |
(3.164) |
![$\displaystyle \left[ \rho\right] =\frac{Vm}{A}=\Omega m=\frac{m}{S}$](img711.gif)
![$\displaystyle \left[ \sigma\right]
=\frac{A}{Vm}=\frac{S}{m}=\frac{1}{\Omega m}$](img712.gif)
Wir betrachten die Bewegung von Ionen
![]() in einer Umgebung von nicht
ionisierten Molekülen
in einer Umgebung von nicht
ionisierten Molekülen
![\includegraphics[width=0.7\textwidth]{elektrostatik-028}](img714.gif)
|
Die Masse der Ionen sei ![]() , ihre Ladung
, ihre Ladung ![]() und die Gesamtzahl im betrachteten Volumenelement
und die Gesamtzahl im betrachteten Volumenelement ![]()
Die Newtonsche Bewegungsgleichung lautet
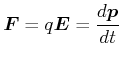 |
(3.165) |
| (3.166) |
Der mittlere Impuls ist
![$\displaystyle M\left\langle \vec{v}\right\rangle =\frac{1}{N}\sum\limits_{j=1}^{N}\left[ M\vec{v}_{j}^{\left( k\right) }+q\vec{E}t_{j}\right]$](img717.gif) |
(3.167) |
Sind die Geschwindigkeiten
![]() isotrop verteilt, mittelt sich der erste Summand zu
null. Unter dieser Annahme ist
isotrop verteilt, mittelt sich der erste Summand zu
null. Unter dieser Annahme ist
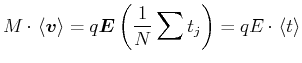 |
(3.168) |
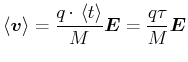 |
(3.169) |
Somit ist bei einer Mischung verschiedener Ladungsträger
Wir haben
![]() gesetzt.
gesetzt.
Das Ohmsche Gesetz gilt, wenn ![]() und
und ![]() unabhängig von
unabhängig von ![]() sind,
sind,
Beispiel: Metall
Wir nehmen an, dass
![]() ist. Dann sind die Geschwindigkeiten nach dem Stossen isotrop verteilt. Die
mittlere Geschwindigkeit der Elektronen ist
ist. Dann sind die Geschwindigkeiten nach dem Stossen isotrop verteilt. Die
mittlere Geschwindigkeit der Elektronen ist
![]() (kinetische Gastheorie). Mit
(kinetische Gastheorie). Mit
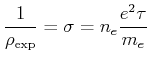 |
(3.172) |
bekommen wir
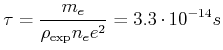 |
(3.173) |
(mit
![]() und
und
![]() für Na-Metall)
für Na-Metall)
Die mittlere freie Weglänge ist dann
| (3.174) |
im Widerspruch zum Ionenabstand von 0.1nm
![]() Lösung: Quantenmechanik
Lösung: Quantenmechanik
|
|
|
|
Bei einem homogenen Ohmschen Leiter mit einer stationären Stromverteilung ist
![]() im Inneren. Dies folgt
aus
im Inneren. Dies folgt
aus
Aus der Eigenschaft
| (3.175) |
erhalten wir im Inneren eines Leiters
| (3.176) |
Dies bedeutet, dass ![]() im Inneren eines homogenen Ohmschen Leiters ein Potentialfeld ist. Die Lösung von
im Inneren eines homogenen Ohmschen Leiters ein Potentialfeld ist. Die Lösung von
| (3.177) |
ist durch die Randbedingungen
![[*]](footnote.gif)
Mit diesen Gleichungen kann man zum Beispiel den Widerstand eines homogenen Leiters berechnen. Bei inhomogenen Leitern müssen wir das Ohmsche Gesetz in seiner Differentialform verwenden. Aus der Kontinuitätsgleichung für stationäre Stromverteilungen Gleichung (3.18) und dem lokalen Ohmschen Gesetz Gleichung (3.26) bekommen wir
| (3.178) |
![\includegraphics[width=0.4\textwidth]{elektrostatik-031}](img750.gif)
|
Wir wenden die Kontinuitätsgleichung Gleichung (3.18) auf die Fläche ![]() an.
an.
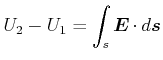 |
(3.181) |
| (3.182) |
| (3.183) |
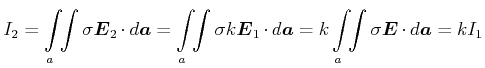 |
(3.184) |
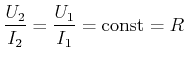 |
(3.185) |
|
Im statischen Falle ist
|
