
Entlang der ![]() -Achse von
-Achse von ![]() bis
bis ![]() sei die Ladung
sei die Ladung ![]() homogen verteilt. Zu berechnen ist das
elektrische Feld für einen Punkt
homogen verteilt. Zu berechnen ist das
elektrische Feld für einen Punkt
![]() auf der
auf der ![]() -Achse!
-Achse!
Die Linienladungsdichte ist
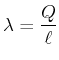
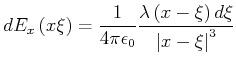
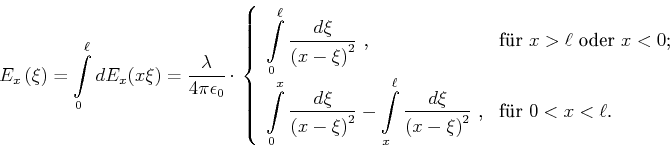
Die Lösung dieser Gleichung ist
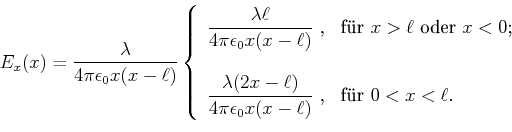
![\includegraphics[width=0.8\textwidth]{linienladung}](img1684.gif)
|
Wir berechnen nun das elektrische Feld entlang der Mittelsenkrechten einer Linienladung der Länge ![]() . Zur
Berechnung legen wir das Koordinationssystem so, dass die Ladungsverteilung von -
. Zur
Berechnung legen wir das Koordinationssystem so, dass die Ladungsverteilung von -
![]() bis
bis
![]() reicht. Aus Symmetriegründen existiert auf der Mittelsenkrechten keine Komponente in
reicht. Aus Symmetriegründen existiert auf der Mittelsenkrechten keine Komponente in
![]() -Richtung. Wir betrachten also die Komponente entlang
-Richtung. Wir betrachten also die Komponente entlang ![]() . Am Punkt
. Am Punkt
![]() ist
ist
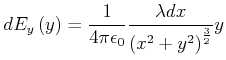
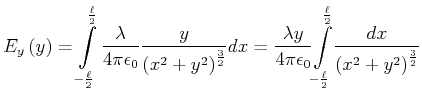
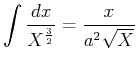
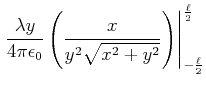 |
|||
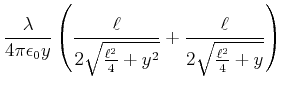 |
|||
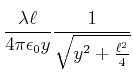 |
|||
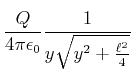 |
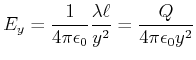
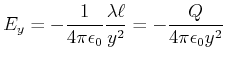
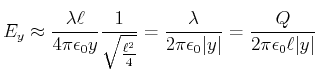
![\includegraphics[width=0.8\textwidth]{linienladung-senkrecht-unendlich}](img1702.gif)
|
