
Up: PHYS3100 Grundkurs IIIb
Klausur
PHYS3100 Grundkurs IIIb (Physik, Wirtschaftsphysik, Physik Lehramt)
Othmar Marti, (othmar.marti@physik.uni-ulm.de)
19. 2. 2004
Prüfungstermin 19. 2. 2004, 09:00 bis 11:00
|
Name |
Vorname |
Matrikel-Nummer |
Kennwort |
| |
|
|
|
| |
|
|
|
| |
|
|
|
Die Prüfungsresultate werden ab 23. 2. 2004 im Sekretariat Experimentelle Physik, N25/540, bekanntgegeben. Dabei
können Sie Ihre Klausur einsehen. Damit Ihr Resultat, sobald vorhanden, per Aushang vor dem Sekretariat
bekanntgegeben werden kann, müssen Sie ein Kennwort (leserlich) angeben.
Vom Korrektor auszufüllen:
|
Aufgabe |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
 |
| Punkte |
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
Note:
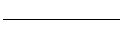 |
Prüfer:
 |
![\includegraphics[width=0.2\textwidth]{uni.eps}](img3.gif) |
Universität Ulm |
Lesen Sie bitte die folgenden Hinweise vollständig und aufmerksam durch,
bevor Sie mit der Bearbeitung der Aufgaben beginnen!.
- Als Hilfsmittel zur Bearbeitung der Klausur sind nur Schreibzeug und Taschenrechner und 3 Blätter (sechs
Seiten, Grösse A4) mit eigener Hand in Handschrift verfasste Notizen zugelassen. Mobiltelefone müssen
ausgeschaltet in einer geschlossenen Tasche oder einem geschlossenen Rucksack aufbewahrt werden!
- Die Klausur umfasst:
- 3 Blätter (6 Seiten) mit 9 Aufgaben.
- 1 Deckblatt bestehend aus einer Titelseite und dieser Hinweisseite.
- Füllen Sie, bevor Sie mit der Bearbeitung der Aufgaben beginnen, das Deckblatt
mit Name, Vorname und Matrikelnummer in leserlicher Druckschrift aus.
- Jede Aufgabe ergibt zwischen 2 und 8 Punkten.
- Benutzen Sie bei der Berechnung von Zahlenwerten die Konstanten aus der Aufgabenstellung, soweit angegeben.
- Schreiben Sie auf jedes Blatt leserlich Ihren Namen, Ihren Vornamen und Ihre Matrikelnummer sowie eine
Seitennummer. Schönschrift beim Schreiben erleichtert die Korrektur.
- Beginnen Sie für jede Aufgabe ein neues Blatt mit Angabe der Aufgabennummer.
Schreiben Sie die zugehörigen Nebenrechnungen ebenfalls auf dieses Blatt. Streichen Sie
ungültige Lösungen deutlich durch. Sollten Sie ausnahmsweise zur Bearbeitung einer
Aufgabe mehrere nicht aufeinanderfolgende Blätter benötigen, so vermerken Sie, wo die
Fortsetzung der Aufgabe zu finden ist.
Viel Erfolg!
- Von welcher Ladungssorte zu welcher Ladungssorte zeigt das elektrische Feld? (0.5 Punkte)
- Wie lautet das komplette Durchflutungsgesetz in differentieller Schreibweise? (0.5 Punkte)
- Geben Sie die Definition des magnetischen Momentes eines Kreisstromes an! (0.5 Punkte)
- Geben Sie die Larmorwinkelgeschwindigkeit für ein Elektron in vektorieller Schreibweise an! (0.5 Punkte)
- Zu welcher Klasse (diamagnetisch, paramagnetisch oder ferromagnetisch) gehört Aluminium?
(0.5 Punkte)
- Ist Eisen diamagnetisch? (0.5 Punkte)
- In einer Vakuumröhre vom Typ
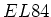 werden Elektronen aus der Ruhe mit einer Spannung von
werden Elektronen aus der Ruhe mit einer Spannung von 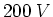 beschleunigt. Geben Sie die kinetische Energie in Elektronenvolt an. (0.5 Punkte)
beschleunigt. Geben Sie die kinetische Energie in Elektronenvolt an. (0.5 Punkte)
- Wir betrachten zwei Ruhesysteme, die sich gegeneinander entlang der
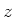 -Achse mit konstanter
Geschwindigkeit
-Achse mit konstanter
Geschwindigkeit 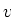 bewegen. Geben Sie die Lorentz-Transformation für das Feld
bewegen. Geben Sie die Lorentz-Transformation für das Feld 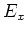 (alle anderen Felder sollen
(alle anderen Felder sollen 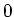 sein) an! (0.5 Punkte)
sein) an! (0.5 Punkte)
- Wir betrachten zwei Ruhesysteme, die sich gegeneinander entlang der
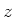 -Achse mit konstanter
Geschwindigkeit
-Achse mit konstanter
Geschwindigkeit 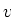 bewegen. Geben Sie die Lorentz-Transformation für das Feld
bewegen. Geben Sie die Lorentz-Transformation für das Feld 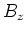 (alle anderen Felder sollen
(alle anderen Felder sollen 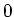 sein) an! (0.5 Punkte)
sein) an! (0.5 Punkte)
- Geben Sie die Definition der Elektromotorischen Kraft in einem Stromkreis an. (0.5 Punkte)
- Erklären Sie in Worten die Funktion einer Zündspule bei einem Otto-Motor. (Sie sollten dazu
nicht mehr als vier Zeilen benötigen.) (0.5 Punkte)
- Erklären Sie in Worten, warum bei einem perfekten kristallinen Leiter (Durchmesser
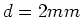 , Länge
, Länge 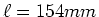 )
bei
)
bei 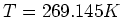 der Strom nicht unendlich gross wird,
wenn eine Spannung von
der Strom nicht unendlich gross wird,
wenn eine Spannung von
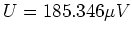 zwischen den beiden
zwischen den beiden 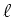 entfernten Enden angelegt wird.
(Sie sollten dazu
nicht mehr als fünf Zeilen benötigen.) (0.5 Punkte)
entfernten Enden angelegt wird.
(Sie sollten dazu
nicht mehr als fünf Zeilen benötigen.) (0.5 Punkte)
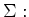 6 Punkte
6 Punkte
- Die folgenden Punkte sind mit geradlinigen Leitern verbunden. In der folgenden Aufstellung sind die Koordinaten
in einem rechtshändigen kartesischen Koordinatensystem angegeben. Die
Einheit ist
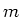 .
.
Die Leiterschlaufe ist
 . In ihren perfekten Leitern fliesst der Strom
. In ihren perfekten Leitern fliesst der Strom 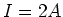 von
von 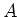 nach
nach
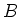 und weiter.
und weiter.
- Zeichnen Sie die Leiterschlaufe mit dem Koordinatensystem und vergessen Sie die Skalen und
Einheiten nicht. (0.5 Punkte)
- Berechnen Sie das resultierende magnetische Moment in vektorieller Schreibweise. (1 Punkte)
- Geben Sie den Betrag des Momentes an (0.5 Punkte)
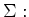 2 Punkte
2 Punkte
- Gegeben sei die folgende Schaltung:
![\includegraphics[width=0.6\textwidth]{klaus-04-02-19-2.eps}](img23.gif)
Der Schalter sei in den folgenden Stellungen:
- Geben Sie die Differentialgleichung für
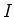 , dem Strom durch den Widerstand, für
, dem Strom durch den Widerstand, für 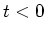 und
und 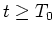 an. (0.5 Punkte)
an. (0.5 Punkte)
- Geben Sie die Differentialgleichung für
 , dem Strom durch den Widerstand, für
, dem Strom durch den Widerstand, für  an. (0.5 Punkte)
an. (0.5 Punkte)
- Lösen Sie die Differentialgleichung für
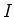 für alle Zeiten. Berechnen Sie daraus
für alle Zeiten. Berechnen Sie daraus 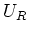 . (1.5 Punkte)
. (1.5 Punkte)
- Verwenden Sie die Anfangsbedingung für
 um
um 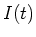 für
für
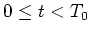 anzugeben. (0.5 Punkte)
anzugeben. (0.5 Punkte)
- Verwenden Sie die Anfangsbedingung für
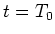 um
um 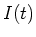 für
für 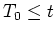 anzugeben. (1.5 Punkte)
anzugeben. (1.5 Punkte)
- Skizzieren Sie die Lösung für
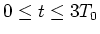 (Grösse der Zeichnung mindestens
(Grösse der Zeichnung mindestens
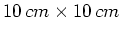 ), wenn
), wenn
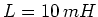 ,
, 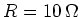 ,
, 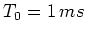 und
und 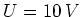 sind. Geben Sie als Referenz die Spannung
sind. Geben Sie als Referenz die Spannung 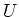 in der Zeichnung
an. (0.5 Punkte)
in der Zeichnung
an. (0.5 Punkte)
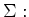 5 Punkte
5 Punkte
- Eine Probeladung
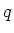 sei zwischen zwei unendlich ausgedehnten perfekt leitfähigen Halbräumen
eingebracht. Die Oberflächen der beiden Halbräume sind parallel und haben den Abstand
sei zwischen zwei unendlich ausgedehnten perfekt leitfähigen Halbräumen
eingebracht. Die Oberflächen der beiden Halbräume sind parallel und haben den Abstand 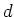 .
.
![\includegraphics[width=0.6\textwidth]{klaus-04-02-19-3.eps}](img46.gif)
- Wir betrachten nur die Oberflächenladungsdichten
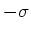 und
und 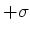 und denken uns die metallischen Halbräume weg.
Geben Sie die potentielle Energie von
und denken uns die metallischen Halbräume weg.
Geben Sie die potentielle Energie von 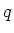 als Funktion von
als Funktion von 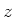 (
(
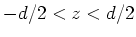 ) an. Legen Sie dabei den Nullpunkt
der
) an. Legen Sie dabei den Nullpunkt
der 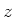 -Skala in die Mitte zwischen den beiden Halbräumen. (1 Punkt)
-Skala in die Mitte zwischen den beiden Halbräumen. (1 Punkt)
- Geben Sie nun die potentielle Energie von
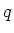 als Funktion von
als Funktion von 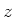 (
(
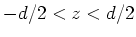 ) an, wenn die
Oberflächenladungsdichten
) an, wenn die
Oberflächenladungsdichten 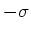 und
und 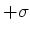 an der Oberfläche von metallischen Halbräumen
liegen. Betrachten Sie nur die zusätzlichen Terme (im Vergleich zur vorigen Aufgabe) erster Ordnung.
(1 Punkt)
an der Oberfläche von metallischen Halbräumen
liegen. Betrachten Sie nur die zusätzlichen Terme (im Vergleich zur vorigen Aufgabe) erster Ordnung.
(1 Punkt)
- Bildladungen im Metall
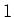 erzeugen im Metall
erzeugen im Metall 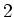 weitere Bildladungen, und umgekehrt. Berechnen
Sie die potentielle Energie von
weitere Bildladungen, und umgekehrt. Berechnen
Sie die potentielle Energie von 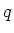 als Funktion von
als Funktion von 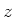 (
(
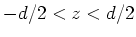 ) bis einschliesslich der zweiten
Bildladung auf beiden Seiten. (1 Punkt)
) bis einschliesslich der zweiten
Bildladung auf beiden Seiten. (1 Punkt)
 3 Punkte
3 Punkte
- Gegeben ist
- Berechnen Sie
 in kartesischen Koordinaten. (1 Punkt)
in kartesischen Koordinaten. (1 Punkt)
- Geben Sie ein Vektorfeld
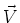 an, so dass
an, so dass
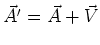 ist und so dass
ist und so dass
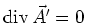 ist. (1 Punkt)
ist. (1 Punkt)
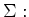 2 Punkte
2 Punkte
- Eine Kompassnadel mit dem Trägheitsmoment
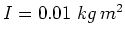 und dem magnetischen Moment
und dem magnetischen Moment
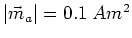 ist im Ursprung des
kartesischen Koordinatensystems um die
ist im Ursprung des
kartesischen Koordinatensystems um die 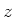 -Achse drehbar gelagert. Eine homogenes magnetisches Feld
-Achse drehbar gelagert. Eine homogenes magnetisches Feld
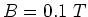 zeigt parallel zur
zeigt parallel zur 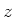 -Achse und zeige in die positive Richtung.
-Achse und zeige in die positive Richtung.
- Geben Sie die Differentialgleichung der Drehbewegung an. (1 Punkt)
- Berechnen Sie die Schwingungskreisfrequenz
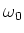 für kleine Amplituden. (1 Punkt)
für kleine Amplituden. (1 Punkt)
 2 Punkte
2 Punkte
- Welche maximale Kraft übt Licht mit einer zeitlich gemittelten Intensität von
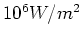 auf ein
einfach geladenes Ion im Vakuum aus?
auf ein
einfach geladenes Ion im Vakuum aus?
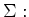 2 Punkte
2 Punkte
- Zwei Punktladungen
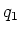 und
und 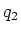 sind an der Peripherie einer mit der
Winkelgeschwindigkeit
sind an der Peripherie einer mit der
Winkelgeschwindigkeit 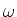 um die
um die 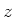 -Achse rotierenden Scheibe vom Radius
-Achse rotierenden Scheibe vom Radius 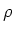 diametral gegenüber
befestigt.
diametral gegenüber
befestigt.
![\includegraphics[width=0.4\textwidth]{klaus-04-02-19-4.eps}](img64.gif)
Es ist
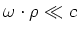 und
und 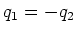 . Für
. Für 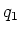 ist
ist
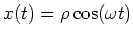 und
und
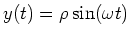 .
.
- Berechnen Sie das Strahlungsfeld an einem Punkt
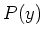 auf der (raumfesten)
auf der (raumfesten)
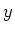 -Achse, wobei
-Achse, wobei 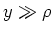 ist. (2 Punkte)
ist. (2 Punkte)
- Geben Sie in einer Skizze an, wie sich die elektrischen Felder in der
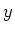 -Richtung ausbreiten
(entsprechend der Lösung aus der Aufgabe 8a). (0.5 Punkte)
-Richtung ausbreiten
(entsprechend der Lösung aus der Aufgabe 8a). (0.5 Punkte)
- Berechnen Sie das Strahlungsfeld an einem Punkt
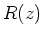 auf der (raumfesten)
auf der (raumfesten)
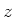 -Achse, wobei
-Achse, wobei 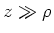 ist. (1 Punkt)
ist. (1 Punkt)
- Geben Sie in einer Skizze an, wie sich die elektrischen Felder in der
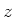 -Richtung ausbreiten
(entsprechend der Lösung aus der Aufgabe 8c). (0.5 Punkte)
-Richtung ausbreiten
(entsprechend der Lösung aus der Aufgabe 8c). (0.5 Punkte)
- Berechnen Sie die Felder für die Anordnung aus der Aufgabe 8a), wenn
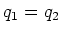 ist.
(1 Punkt)
ist.
(1 Punkt)
- Berechnen Sie die Felder für die Anordnung aus der Aufgabe 8c), wenn
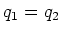 ist.
(1 Punkt)
ist.
(1 Punkt)
 6 Punkte
6 Punkte
- Die folgende Schaltung soll berechnet werden:
![\includegraphics[width=0.65\textwidth]{klaus-01.eps}](img75.gif)
Der Schalter 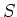 ist für
ist für 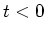 offen und wird bei
offen und wird bei 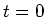 geschlossen. Der Transformator ist auf einen
Eisenkern mit dem Querschnitt
geschlossen. Der Transformator ist auf einen
Eisenkern mit dem Querschnitt 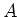 gewickelt.
Das Eisen bewirkt, dass das Magnetfeld
gewickelt.
Das Eisen bewirkt, dass das Magnetfeld 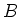 und der Fluss
und der Fluss 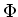 nur im Eisen existiert. Die Primärwicklung hat
nur im Eisen existiert. Die Primärwicklung hat 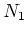 Windungen, die Sekundärwicklung
Windungen, die Sekundärwicklung 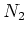 Windungen.
Die Spulen haben jeweils die Länge
Windungen.
Die Spulen haben jeweils die Länge 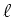 .
.
- Geben Sie die Induktivität der Primärwicklung an. (0.5 Punkte)
- Geben Sie die Induktivität der Sekundärwicklung an. (0.5 Punkte)
- Geben Sie die Gegeninduktivität zwischen der Primär- und der Sekundärwicklung an.
Drücken Sie das Resultat mit
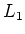 und
und 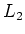 aus. (1 Punkt)
aus. (1 Punkt)
- Wie lautet das Differentialgleichung für den Strom
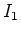 der Primärseite? (0.5 Punkte)
der Primärseite? (0.5 Punkte)
- Wie lautet das Differentialgleichung für den Strom
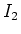 der Sekundärseite? (0.5 Punkte)
der Sekundärseite? (0.5 Punkte)
- Wenn Sie richtig gerechnet haben, kommt
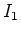 in der Gleichung für die Sekundärseite nur einmal vor.
Wandeln Sie die Gleichungen für die Primärseite und die Sekundärseite so um, dass Sie in der Gleichung für die Primärseite
in der Gleichung für die Sekundärseite nur einmal vor.
Wandeln Sie die Gleichungen für die Primärseite und die Sekundärseite so um, dass Sie in der Gleichung für die Primärseite
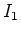 eliminieren können. Geben Sie für
eliminieren können. Geben Sie für  die Differentialgleichung für
die Differentialgleichung für 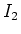 an! (2.5 Punkte)
an! (2.5 Punkte)
- Verwenden Sie das Resultat aus dem Teil 9c und formen Sie die Gleichung für
 so um, dass die Schwingungskreisfrequenz
so um, dass die Schwingungskreisfrequenz 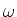 auftritt,
indem Sie für den Strom
auftritt,
indem Sie für den Strom 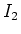 einen komplexen Ansatz machen. (1 Punkt)
einen komplexen Ansatz machen. (1 Punkt)
- Berechnen Sie die reelle Schwingungsfrequenz der Eigenschwingung der Schaltung. (1 Punkt)
- Wie ist das asymptotische Verhalten der Spannung am Widerstand
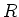 ,
, 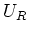 und am Kondensator
und am Kondensator 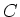 ,
, 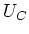 für
für
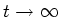 ? (0.5 Punkte)
? (0.5 Punkte)
 8 Punkte
8 Punkte
Gesamt-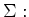 36 Punkte
36 Punkte
- von der positiven zur negativen Ladung (0.5 Punkte)
-
(0.5 Punkte)
-
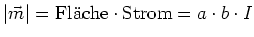 (Seite 100) (0.5 Punkte)
(Seite 100) (0.5 Punkte)
-
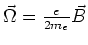 (Seite 144) (0.5 Punkte)
(Seite 144) (0.5 Punkte)
- Aluminium ist paramagnetisch. (0.5 Punkte)
- Eisen ist auch diamagnetisch, der Effekt ist aber sehr viel kleiner als der Ferromagnetismus. (0.5 Punkte)
-
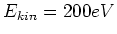 (0.5 Punkte)
(0.5 Punkte)
- Wir hatten die Lorentztransformationen mit einer Geschwindigkeit
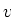 entlang
entlang 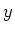 berechnet. Hier sollen
sie nun für
berechnet. Hier sollen
sie nun für 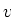 entlang
entlang 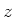 angegeben werden. Das ursprüngliche Koordinatensystem mit
angegeben werden. Das ursprüngliche Koordinatensystem mit 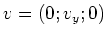 wird durch eine Drehung um die
wird durch eine Drehung um die 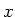 -Achse um
-Achse um 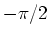 auf das Koordinatensystem
auf das Koordinatensystem
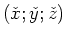 transformiert, wobei
transformiert, wobei
ist. Also erhalten wir
(0.5 Punkte)
- Hier ist
(0.5 Punkte)
-
(0.5 Punkte)
- In einer Zündspule wird Energie im Magnetfeld gespeichert. Beim Abschalten des Stromes entsteht
wegen der kurzen Zeit eine sehr hohe Induktionsspannung, die durch die Ableitung des Flusses nach der Zeit
definiert ist. (0.5 Punkte)
- Elektronen können sich im quantenmechanischen Bild nur an Fehlstellen, nicht aber an perfekten
periodischen Anordnungen wie in einem Kristall streuen und so ihre kinetische Energie abgeben. Bei
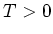 schwingen alle Atome um ihre Ruheposition, das Gitter ist also nicht mehr perfekt. (0.5 Punkte)
schwingen alle Atome um ihre Ruheposition, das Gitter ist also nicht mehr perfekt. (0.5 Punkte)
- Die Skizze sieht so aus:
![\includegraphics[height=0.5\textwidth]{klaus-04-02-19-1.eps}](img107.gif) (0.5 Punkte)
(0.5 Punkte)
- Das gesamte magnetische Moment ist äquivalent zum magnetischen Moment von drei Schlaufen zusammen,
da sich auf den Koordinatenachsen die Ströme aufheben. Es sei
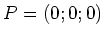 . Wir erhalten
. Wir erhalten
| Schlaufe |
Richtung |
Fläche |
|
| ABCPA |
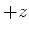 |
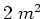 |
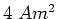 |
| CDEPC |
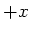 |
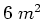 |
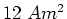 |
| EFAPE |
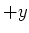 |
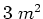 |
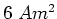 |
(0.5 Punkte)
sind. Das einzelne magnetische Moment ist durch
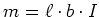 gegeben.
Das gesamte magnetische Moment ist
gegeben.
Das gesamte magnetische Moment ist
(0.5 Punkte)
-
(0.5 Punkte)
- Hier gilt
also
(0.5 Punkte)
- Hier gilt
also
(0.5 Punkte)
- Ansatz:
Also ist die homogene Lösung
oder
und damit
(0.5 Punkte)
Partikuläre Lösung
(0.5 Punkte)
Also ist für
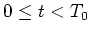
(0.5 Punkte)
- Für
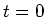 ist
ist 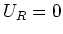 und daraus
und daraus
Also
(0.5 Punkte)
- Es ist
(0.5 Punkte)
Das ist die Anfangsbedingung für die homogene Lösung. Für 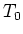 muss also gelten
muss also gelten
Also
(0.5 Punkte)
Also
(0.5 Punkte)
-
![\includegraphics[width=0.6\textwidth]{klaus-2004-02-19.eps}](img139.gif)
(0.5 Punkte)
- Das elektrische Feld einer Oberflächenladungsdichte ist
Die Felder der beiden Oberflächenladungen addieren sich, so dass
(0.5 Punkte)
Das Feld zeigt nach rechts.
Die potentielle Energie ist dann
(0.5 Punkte)
- Hier treten Bildladungen auf. Die eine Bildladung liegt bei
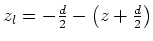 . Der Abstand zur Ladung ist
. Der Abstand zur Ladung ist 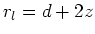 .
Die zweite Bildladung liegt bei
.
Die zweite Bildladung liegt bei
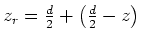 . Der Abstand ist
. Der Abstand ist 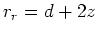 .
Die Bildladung ist jeweils
.
Die Bildladung ist jeweils 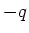 . Die potentielle Energie ist
. Die potentielle Energie ist
(0.5 Punkte)
und
Also ist die gesamte potentielle Energie
oder
(0.5 Punkte)
- Die Bildladungen der Bildladung liegen bei
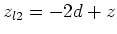 , der Abstand ist also
, der Abstand ist also
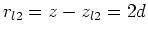 und
und 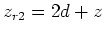 und damit
und damit 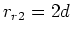 . Die zweite Bildladung ist wieder
jeweils
. Die zweite Bildladung ist wieder
jeweils
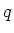 . Also haben wir zusätzlich die potentielle Energie
. Also haben wir zusätzlich die potentielle Energie
(0.5 Punkte)
Damit ist die gesamte potentielle Energie
(0.5 Punkte)
Die folgende Skizze (zur Information) zeigt den Kurvenverlauf:
![\includegraphics[width=0.7\textwidth]{klaus-04-02-19-10.eps}](img158.gif)
- Die Lösung ist
(0.5 Punkte)
(0.5 Punkte)
- Es muss gelten,
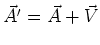 . Die Divergenz von
. Die Divergenz von 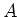 ist
ist
(0.5 Punkte)
Gesucht wird also ein Vektorfeld, bei dem
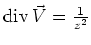 ist. Dies ist
ist. Dies ist
(0.5 Punkte)
da bei
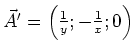 die Divergenz null ist.
die Divergenz null ist.
- Das mechanische Drehmoment ist
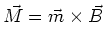 oder
oder
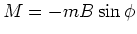 , wenn man die Richtungen berücksichtigt. (0.5 Punkte)
, wenn man die Richtungen berücksichtigt. (0.5 Punkte)
Weiter gilt
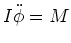 .
Also ist
.
Also ist
(0.5 Punkte)
- Für kleine Amplituden ist
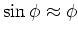 . Also
. Also
(0.5 Punkte)
Also ist
(0.5 Punkte)
- Nach der Vorlesung Grundlagen IIIa (Seite 79) gilt
(0.5 Punkte)
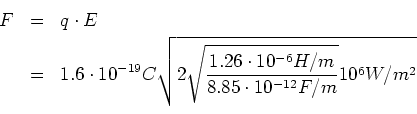
Die Ladung eines einfach geladenen Ions beträgt 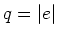
Also ist (mit
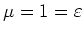 )
)
(0.5 Punkte)
oder eingesetzt:
(0.5 Punkte)
(0.5 Punkte)
- Das Strahlungsfeld im Abstand
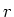 zur Zeit
zur Zeit 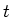 ist
ist
wobei 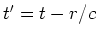 und
und 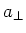 die Beschleunigungskomponente senkrecht zur Beobachtungsrichtung ist. (0.5 Punkte)
die Beschleunigungskomponente senkrecht zur Beobachtungsrichtung ist. (0.5 Punkte)
- Nur die
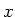 -Komponente zählt.
-Komponente zählt.
für die erste Ladung und
für die zweite Ladung. (0.5 Punkte)
- Da
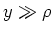 ist
ist 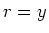 .
.
(1 Punkt)
-
![\includegraphics[width=0.5\textwidth]{klaus-04-02-19-5.eps}](img187.gif) (0.5 Punkte)
(0.5 Punkte)
- Hier ist die wirksame Beschleunigung sowohl in der
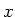 - wie auch in der
- wie auch in der 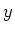 -Richtung.
-Richtung.
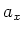 und
und 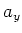 sind um
sind um 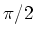 phasenverschoben. (0.5 Punkte)
phasenverschoben. (0.5 Punkte)
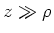
-
(0.5 Punkte)
- Dies ist eine zirkular polarisierte Strahlung.
-
![\includegraphics[width=0.5\textwidth]{klaus-04-02-19-6.eps}](img192.gif) (0.5 Punkte)
(0.5 Punkte)
- Wenn
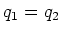 dann ist
dann ist 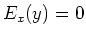 (1 Punkt)
(1 Punkt)
- Wenn
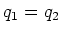 dann ist
dann ist
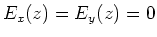 (1 Punkt)
(1 Punkt)
- Die Induktivität ist
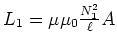 . (0.5 Punkte)
. (0.5 Punkte)
- Die Induktivität ist
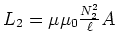 . (0.5 Punkte)
. (0.5 Punkte)
- Die Induktivität ist
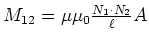 (0.5 Punkte)
(0.5 Punkte)
oder
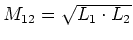 . (0.5 Punkte)
. (0.5 Punkte)
- Im Primärkreis haben wir
(0.5 Punkte)
- Im Sekundärkreis haben wir
mit 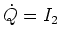 oder
oder
(0.5 Punkte)
- Wir leiten die Gleichung des Primärkreises zweimal ab.
(0.5 Punkte)
- Die ursprüngliche Gleichung des Sekundärkreises enthält
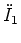 .
Wir leiten die Gleichung des Sekundärkreises einmal ab und erhalten eine Gleichung für
.
Wir leiten die Gleichung des Sekundärkreises einmal ab und erhalten eine Gleichung für
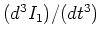 .
.
(0.5 Punkte)
- Diese Gleichung sowie die Originalgleichung für den Sekundärkreis setzen wir in die zweimal abgeleitete Gleichung des Primärkreises ein.
(0.5 Punkte)
- Da
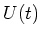 für
für 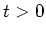 konstant ist, ist die
konstant ist, ist die 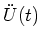 überall ausser bei
überall ausser bei 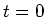 null. Hier wird
die Lösung für
null. Hier wird
die Lösung für 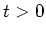 gesucht.
gesucht.
-
(0.5 Punkte)
- Wir ordnen die Ableitungen
(0.5 Punkte)
- Mit
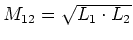 lautet die Differentialgleichung
lautet die Differentialgleichung
- oder
(0.5 Punkte)
- Dies ist die gewöhnliche Schwingungsdifferentialgleichung. Wir setzen
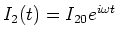
-
- Unter der Annahme,dass
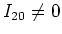 bekommen wir
bekommen wir
(0.5 Punkte)
- Wir lösen nach
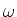 auf
auf
- Setzt man die Lösung in den Ansatz ein, so sieht man, dass der komplexe Summand die Dämpfung
darstellt. Die reelle Schwingungsfrequenz ist:
(0.5 Punkte)
- Die positive Lösung ist
(0.5 Punkte)
- Für grosse Zeiten geht
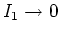 und damit auch
und damit auch
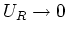 . Damit ist auch
. Damit ist auch
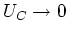 . (0.5 Punkte)
. (0.5 Punkte)
| Punkte |
Note |
Anzahl |
| |
|
|
| 0-11,5 |
5 |
|
| |
|
|
| 12-13,5 |
4 |
|
| |
|
|
| 14-15,5 |
3,7 |
|
| |
|
|
| 16-17,5 |
3,3 |
|
| |
|
|
| 18-19 |
3 |
|
| |
|
|
| 19,5-21 |
2,7 |
|
| |
|
|
| 21,5-23 |
2,3 |
|
| |
|
|
| 23,5-24,5 |
2 |
|
| |
|
|
| 25-26,5 |
1,7 |
|
| |
|
|
| 27-28,5 |
1,3 |
|
| |
|
|
| 29-36 |
1 |
|
| |
|
|
| Aufgabe |
Punkte |
| 1 |
6 |
| 2 |
2 |
| 3 |
5 |
| 4 |
3 |
| 5 |
2 |
| 6 |
2 |
| 7 |
2 |
| 8 |
6 |
| 9 |
8 |
 |
36 |
Klausur
PHYS3100 Grundkurs IIIb (Physik, Wirtschaftsphysik, Physik Lehramt)
This document was generated using the
LaTeX2HTML translator Version 99.2beta8 (1.46)
Copyright © 1993, 1994, 1995, 1996,
Nikos Drakos,
Computer Based Learning Unit, University of Leeds.
Copyright © 1997, 1998, 1999,
Ross Moore,
Mathematics Department, Macquarie University, Sydney.
The command line arguments were:
latex2html klausur
The translation was initiated by marti on 2004-02-20


Up: PHYS3100 Grundkurs IIIb
Othmar Marti
Experimentelle Physik
Universiät Ulm
![\includegraphics[width=0.2\textwidth]{uni.eps}](img3.gif)

![\includegraphics[width=0.6\textwidth]{klaus-04-02-19-2.eps}](img23.gif)
![\includegraphics[width=0.6\textwidth]{klaus-04-02-19-3.eps}](img46.gif)
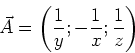
![\includegraphics[width=0.4\textwidth]{klaus-04-02-19-4.eps}](img64.gif)
![\includegraphics[width=0.65\textwidth]{klaus-01.eps}](img75.gif)
![]() 36 Punkte
36 Punkte
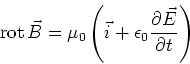
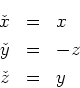
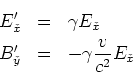
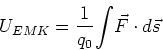
![\includegraphics[height=0.5\textwidth]{klaus-04-02-19-1.eps}](img107.gif) (0.5 Punkte)
(0.5 Punkte)
![\includegraphics[width=0.6\textwidth]{klaus-2004-02-19.eps}](img139.gif)
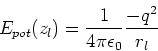
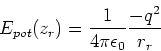
![\begin{displaymath}E_{pot}(z) = \frac{\sigma q z}{\epsilon_0}+\frac{-q^2}{4\pi\e...
...^2}{4\pi\epsilon_0}
\left[\frac{1}{d-2z}+\frac{1}{d+2z}\right]\end{displaymath}](img150.gif)
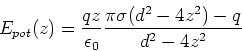
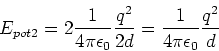
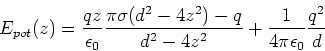
![\includegraphics[width=0.7\textwidth]{klaus-04-02-19-10.eps}](img158.gif)
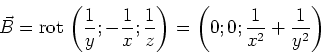
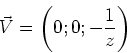
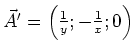 die Divergenz null ist.
die Divergenz null ist.
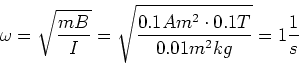
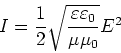
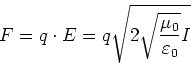
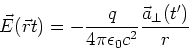
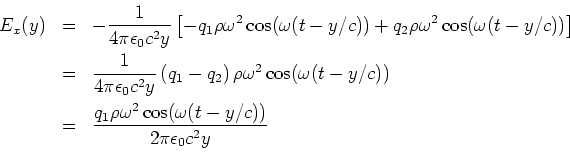
![\includegraphics[width=0.5\textwidth]{klaus-04-02-19-5.eps}](img187.gif) (0.5 Punkte)
(0.5 Punkte)
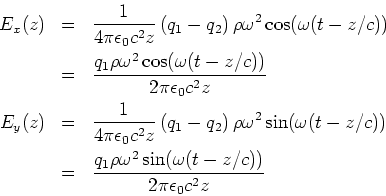
![\includegraphics[width=0.5\textwidth]{klaus-04-02-19-6.eps}](img192.gif) (0.5 Punkte)
(0.5 Punkte)
![\begin{displaymath}\frac{d^2U(t)}{dt^2} + M_{12}\frac{d^3
I_2}{dt^3}=\frac{R}{M...
...eft[L_2 \frac{d^3 I_2}{dt^3}+\frac{1}{C}\frac{d I_2}{dt}\right]\end{displaymath}](img207.gif)
![\begin{displaymath}M_{12}\frac{d^3
I_2}{dt^3}=\frac{R}{M_{12}}\left[L_2\frac{d^...
...eft[L_2 \frac{d^3 I_2}{dt^3}+\frac{1}{C}\frac{d I_2}{dt}\right]\end{displaymath}](img210.gif)
![\begin{displaymath}\left[M_{12}-\frac{L_1 L_2}{M_{12}}\right]\frac{d^3
I_2}{dt^...
...}+
\frac{L_1}{M_{12} C}\frac{d I_2}{dt}+\frac{R }{M_{12} C}I_2\end{displaymath}](img211.gif)
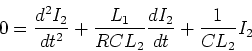
![\begin{displaymath}\omega = \frac{-i\frac{L_1}{RCL_2}\pm
\sqrt{\left[i\frac{L_1}{RCL_2}\right]^2-4(-1)\frac{1}{CL_2}}}{-2}\end{displaymath}](img218.gif)
![\begin{displaymath}\omega = \frac{\pm
\sqrt{4\frac{1}{CL_2}-\left[\frac{L_1}{RC...
... = \mp
\sqrt{\frac{1}{CL_2}-\left[\frac{L_1}{2RCL_2}\right]^2}\end{displaymath}](img219.gif)