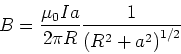

Up: PHYS3100 Grundkurs IIIb
Übungsblatt 07
PHYS3100 Grundkurs IIIb (Physik, Wirtschaftsphysik, Physik Lehramt)
Othmar Marti, (othmar.marti@physik.uni-ulm.de)
2. 2. 2004 oder 9. 2. 2004
- Berechnen Sie für die unten stehende Schaltung die am Widerstand abfallende Spannung
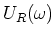 .
.
![\includegraphics[width=0.45\textwidth]{ue-04-07-01.eps}](img2.gif)
- Berechnen Sie für die unten stehende Schaltung die an allen Bauteilen abfallenden Spannungen.
![\includegraphics[width=0.6\textwidth]{ue-04-07-02.eps}](img3.gif)
- Eine Kompassnadel habe die Länge
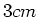 , den Radius
, den Radius 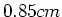 und die Dichte
und die Dichte 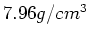 . Sie kann horizontal frei
rotieren, und die horizontale Komponente des Magnetfeldes betrage
. Sie kann horizontal frei
rotieren, und die horizontale Komponente des Magnetfeldes betrage 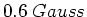 . Bei kleiner Auslenkung
ergebe sich eine harmonische Schwingung um den Mittelpunkt mit
. Bei kleiner Auslenkung
ergebe sich eine harmonische Schwingung um den Mittelpunkt mit 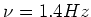 .
.
- Wie gross ist das magnetische Dipolmoment der Nadel?
- Wie gross ist die Magnetisierung
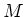
- Wie gross ist der Ampèresche Strom an der Oberfläche der Nadel?
- Ein Eisenstab mit der Länge
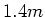 und dem Durchmesser
und dem Durchmesser 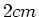 habe die homogene Magnetisierung
habe die homogene Magnetisierung
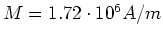 , die entlang des Stabes ausgerichtet sei. Der Stab sei an einem dünnen Faden aufgehängt und
befinde sich in der Mitte (koaxial) einer langen Spule in Ruhe. Durch die Spule werde kurzzeitig ein
Strom geschickt, durch dessen Magnetfeld der Stab plötzlich entmagnetisiert werde. Wie gross ist die
Winkelgeschwindigkeit des Stabes unter der Annahme, dass sein Drehimpuls erhalten bleibe? Nehmen Sie
an, dass
, die entlang des Stabes ausgerichtet sei. Der Stab sei an einem dünnen Faden aufgehängt und
befinde sich in der Mitte (koaxial) einer langen Spule in Ruhe. Durch die Spule werde kurzzeitig ein
Strom geschickt, durch dessen Magnetfeld der Stab plötzlich entmagnetisiert werde. Wie gross ist die
Winkelgeschwindigkeit des Stabes unter der Annahme, dass sein Drehimpuls erhalten bleibe? Nehmen Sie
an, dass
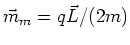 gelte, wobei
gelte, wobei 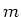 die Masse des Elektrons und
die Masse des Elektrons und 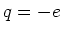 dessen Ladung
ist. Der Effekt, der dieser Aufgabe zugrunde liegt, ist der Einstein-De Haas-Effekt.
dessen Ladung
ist. Der Effekt, der dieser Aufgabe zugrunde liegt, ist der Einstein-De Haas-Effekt.
- Zwei Punktladungen
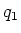 und
und 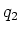 sind an der Peripherie einer mit der
Winkelgeschwindigkeit
sind an der Peripherie einer mit der
Winkelgeschwindigkeit 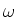 um die
um die 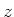 -Achse rotierenden Scheibe vom Radius
-Achse rotierenden Scheibe vom Radius 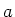 diametral gegenüber befestigt.
Es ist
diametral gegenüber befestigt.
Es ist
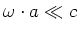 und
und 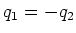 . Es ist
. Es ist
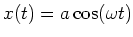 und
und
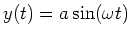 .
.
- Berechnen Sie das Strahlungsfeld an einem Punkt
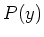 auf der (raumfesten)
auf der (raumfesten)
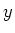 -Achse, wobei
-Achse, wobei 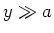 ist.
ist.
- Geben Sie eine Skizze der Felder aus der Aufgabe 5a) an.
- Berechnen Sie das Strahlungsfeld an einem Punkt
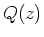 auf der (raumfesten)
auf der (raumfesten)
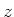 -Achse, wobei
-Achse, wobei 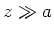 ist.
ist.
- Geben Sie eine Skizze der Felder aus der Aufgabe 5c) an.
- Berechnen Sie die Felder für die Anordnung aus der Aufgaben 5a), wenn
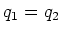 ist.
ist.
- Berechnen Sie die Felder für die Anordnung aus der Aufgaben 5c), wenn
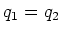 ist.
ist.
- Ein Schwingkreis wird als empfindliches Nachweissystem eines zeitlich harmonischen
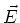 -Feldes
verwendet. Ein Plattenkondensator (Plattenabstand
-Feldes
verwendet. Ein Plattenkondensator (Plattenabstand 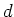 , Kapazität
, Kapazität 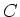 ) befindet sich im räumlich homogenen
) befindet sich im räumlich homogenen
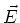 -Feld
-Feld
wobei 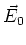 senkrecht zur Fläche des Plattenkondensators orientiert ist. Eine Spule
(Selbstinduktion
senkrecht zur Fläche des Plattenkondensators orientiert ist. Eine Spule
(Selbstinduktion 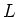 ) und ein Ohmscher Widerstand
) und ein Ohmscher Widerstand 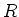 , beide ausserhalb des elektrischen Feldes,
ergänzen den Plattenkondensator zu einem Schwingkreis.
, beide ausserhalb des elektrischen Feldes,
ergänzen den Plattenkondensator zu einem Schwingkreis.
![\includegraphics[width=0.4\textwidth]{nachklausur-03.eps}](img38.gif)
- Stellen Sie die Differentialgleichung für die im Schwingkreis bewegte Ladung
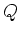 ohne äusseres Feld
auf.
ohne äusseres Feld
auf.
- Modifizieren Sie diese Differentialgleichung so, dass das äussere Feld als
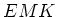 wirkt.
Schreiben Sie dazu das anregende Feld
wirkt.
Schreiben Sie dazu das anregende Feld
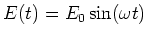 als komplexe Funktion, aber so, dass
der Realteil dieser Funktion gerade der gegebenen reellen Anregung entspricht.
als komplexe Funktion, aber so, dass
der Realteil dieser Funktion gerade der gegebenen reellen Anregung entspricht.
- Wandeln Sie die Differentialgleichung in eine Differentialgleichung für den Strom
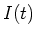 um.
um.
- Berechnen Sie für die Frequenz
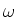 der Anregung den komplexen Strom
der Anregung den komplexen Strom
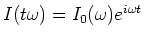 .
.
- Zwischenrechnung: Wenn der Strom
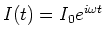 ist (ohne einsetzen), und dieser Strom durch den Widerstand
ist (ohne einsetzen), und dieser Strom durch den Widerstand 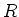 fliesst, was ist dann
die über eine Anzahl
fliesst, was ist dann
die über eine Anzahl
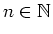 gemittelte thermische Leistung an
gemittelte thermische Leistung an 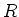 ?
?
- Berechnen Sie die zeitlich gemittelte Leistung
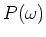 , die als Joulsche
Wärme im Widerstand
, die als Joulsche
Wärme im Widerstand 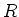 deponiert wird.
deponiert wird.
- Wie gross ist die unbedämpfte Resonanzfrequenz
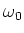 des Schwingkreises?
des Schwingkreises?
- Wie gross ist
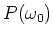 ?
?
- Bestimmen Sie das
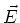 -Feld im Inneren des Plattenkondensators für ein stationäres
äusseres
-Feld im Inneren des Plattenkondensators für ein stationäres
äusseres 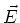 -Feld
-Feld 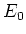 .
.
- Es soll gezeigt werden, dass die allgemeine Formulierung des Ampèreschen Gesetzes
und das Gesetz von Biot-Savart zum gleichen Ergebnis kommen, wenn beide auf
![\includegraphics[width=0.53\textwidth]{ue-07-01.eps}](img51.gif)
angewandt werden.
Zwei Ladungen 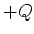 und
und 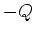 befinden sich im Abstand
befinden sich im Abstand 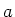 vom Nullpunkt auf der
vom Nullpunkt auf der 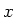 -Achse bei
-Achse bei 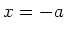 und
und 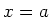 . Entlang der Verbindungslinie fliesst ein Strom
. Entlang der Verbindungslinie fliesst ein Strom 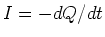 . Der Punkt
. Der Punkt 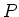 befindet sich
auf der
befindet sich
auf der 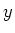 -Achse im Abstand
-Achse im Abstand 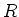 .
.
- Zeigen Sie unter Verwendung
des Gesetzes von Biot-Savart, dass das Magnetfeld am Punkt
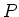 durch
durch
- Ein kreisförmiger Streifen (Mittelpunkt im Ursprung) mit dem Radius
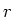 und der Breite
und der Breite 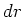 liege in der
liege in der 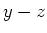 -Ebene. Zeigen Sie, dass der Fluss des elektrischen Feldes durch diesen Streifen
durch
-Ebene. Zeigen Sie, dass der Fluss des elektrischen Feldes durch diesen Streifen
durch
gegeben ist.
- Berechnen Sie mit dem Ergebnis aus 7b den gesamten Fluss
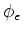 durch die
kreisförmige Ebene mit dem Radius
durch die
kreisförmige Ebene mit dem Radius 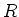 . Es ergibt sich
. Es ergibt sich
- Berechnen Sie den Verschiebungsstrom
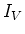 und zeigen Sie, dass
und zeigen Sie, dass
- Berechnen Sie mit dem Ampèreschen Gesetz die Aufgabe 7a und zeigen Sie, dass man
für
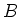 das gleiche Ergebnis erhält.
das gleiche Ergebnis erhält.
- Maschenregel rechts (Vorzeichen)
Maschenregel links
Knotenregel
Aus der ersten Gleichung
und
und damit
Mit
bekommen wir
Wir multiplizieren mit
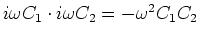 und bekommen
und bekommen
oder
- Wir formen um (
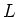 bedeutet für Gleichspannungen und -ströme einen Kurzschluss,
bedeutet für Gleichspannungen und -ströme einen Kurzschluss, 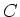 eine Unterbrechung)
eine Unterbrechung)
![\includegraphics[width=0.6\textwidth]{ue-04-07-03.eps}](img86.gif)
Wir haben drei Schlaufen und die entsprechenden Ströme
![\includegraphics[width=0.6\textwidth]{ue-04-07-04.eps}](img87.gif)
Die relevanten Gleichungen sind:
Wir lösen nach 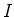 ein und setzen ein
ein und setzen ein
und erhalten
Wir setzen 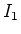 ein
ein
Wir erhalten
Daraus folgt
Wir berechnen 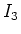
und erhalten
und damit
-
- Das magnetische Moment der
Kompassnadel ist
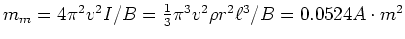 .
.
- Die Magnetisierung ist
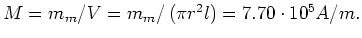
- Die Magnetisierung
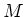 hat die Dimension Stromstärke pro Länge und ist gleich dem
Oberflächenstrom pro Längeneinheit entlang der Nadel; es folgt
hat die Dimension Stromstärke pro Länge und ist gleich dem
Oberflächenstrom pro Längeneinheit entlang der Nadel; es folgt
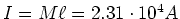 .
.
- Mit dem im Text gegebenen Ergebnis ist der Drehimpulsbetrag
Er ist verknüpft mit dem magnetischen Moment des Stabes, das entlang
dessen Längsachse ausgerichtet ist. Wenn der Stab um diese Achse rotiert, ist sein Drehimpuls 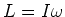 .
Darin ist
.
Darin ist 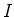 das Trägheitsmoment einer Scheibe. Es folgt
das Trägheitsmoment einer Scheibe. Es folgt
Das setzen wir gleich dem Ausdruck für den
Drehimpuls und erhalten
Das ist eine
äusserst geringe Frequenz.
-
-
![\includegraphics[width=0.6\textwidth]{ue-04-07-05.eps}](img128.gif)
- Hier ist die wirksame Beschleunigung sowohl in der
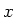 - wie auch in der
- wie auch in der 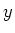 -Richtung.
-Richtung.
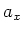 und
und 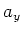 sind um
sind um 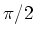 phasenverschoben.
phasenverschoben.
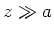
-
und
- Dies ist eine zirkular polarisierte Strahlung.
-
![\includegraphics[width=0.6\textwidth]{ue-04-07-06.eps}](img134.gif)
- Wenn
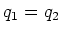 dann ist
dann ist 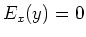
- Wenn
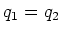 dann ist
dann ist
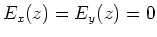
- Die Spannung am Kondensator ist
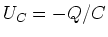
- Die Spannung am Widerstand ist
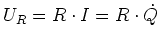
- Die Spannung an der Spule ist
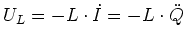
- Maschenregel:
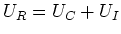 (da nur
(da nur 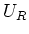 Verbraucher), also
Verbraucher), also
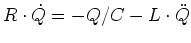
- oder
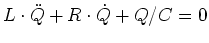
- Das äussere Feld bewirkt über dem Kondensator eine
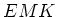 mit der Grösse
mit der Grösse
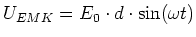
- komplex geschrieben ist
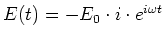 , da ja
, da ja
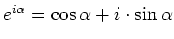 ist.
ist.
- Also ist
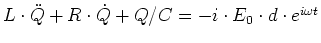
- Es ist
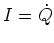 , das heisst, wir leiten einmal ab
, das heisst, wir leiten einmal ab
- Mit
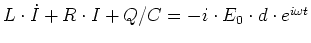 erhalten wir
erhalten wir
-
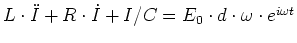
- Wir setzen den Ansatz
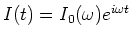 ein
ein
-
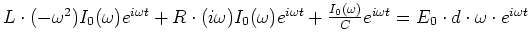
- Wir eliminieren
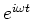 und multiplizieren
und multiplizieren 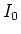 aus
aus
![$I_0(\omega)\left[- L \cdot \omega^2 + i\omega\cdot R +
\frac{1}{C}\right] = E_0\cdot d \cdot \omega $](img155.gif)
- Wir lösen nach
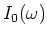 auf
auf
- Normalerweise wird die Gleichung so geschrieben:
- Die momentane Leistung am Widerstand
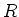 ist
ist
- Gemittelt über eine Anzahl Perioden
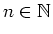 ist
ist
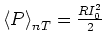
-
- Die ungedämpfte Resonanzfrequenz ist
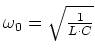
- Bei
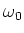 ist
ist
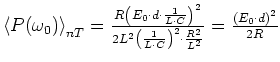
- Ein statisches äusseres Feld bewirkt auf den Kondensatorplatten eine Ladungstrennung. Da im
statischen Falle der Kondensator kurzgeschlossen ist, ist
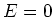 im Inneren, wobei die Ladungen auf den
Platten das äussere Feld kompensieren.
im Inneren, wobei die Ladungen auf den
Platten das äussere Feld kompensieren.
-
- Das Magnetfeld, das am Punkt
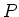 von einem Teilstrom hervorgerufen wird,
ist
von einem Teilstrom hervorgerufen wird,
ist
![$B=\left[ \mu_{0}I/\left( 4\pi
R\right) \right] \left( \sin\theta _{1}+\sin\theta_{2}\right)$](img165.gif) . Die Abbildung zeigt
die entsprechenden Grössen:
. Die Abbildung zeigt
die entsprechenden Grössen:
![\includegraphics[width=0.5\textwidth]{ue-07-02.eps}](img166.gif)
Hier ist
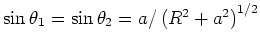 .
.
Daher ist
![$B=\left[\mu_{0}Ia/\left( 2\pi R\right) \right] \left( R^{2}+a^{2}\right)^{-1/2}$](img168.gif) .
.
- Die folgende Abbildung zeigt, wie das elektrische Feld an einem Punkt auf der
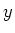 -Achse im
Abstand
-Achse im
Abstand 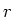 von der
von der 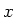 -Achse erhalten wird.
-Achse erhalten wird.
![\includegraphics[width=0.5\textwidth]{ue-07-03.eps}](img169.gif)
Es ist
Die Fläche des Kreises ist 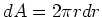 , und es folgt
, und es folgt
.
- Um den elektrischen Fluss heraus, zum Radius
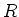 , zu erhalten,
integrieren wir
, zu erhalten,
integrieren wir
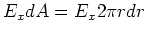 von
von 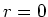 bis
bis 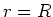 :
:
Damit ist
.
- Nach Definition ist
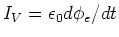 . Jedoch ist im Ausdruck für
. Jedoch ist im Ausdruck für
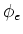 die einzige Grösse, die von der Zeit abhängt,
die einzige Grösse, die von der Zeit abhängt, 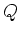 . Mit
. Mit 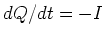 erhalten wir
erhalten wir
![$I_{V}=-I\left[ 1-a/\left(R^{2}+a^{2}\right) ^{1/2}\right] $](img181.gif) und
und
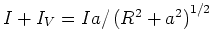 .
.
- Das Gesetz von Ampère besagt, dass das Linienintegral über
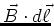 längs eines Kreises vom
Radius
längs eines Kreises vom
Radius 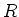 in der
in der 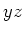 -Ebene mit dem Mittelpunkt am Ursprung, das gleich
-Ebene mit dem Mittelpunkt am Ursprung, das gleich
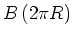 ist,
auch gleich
ist,
auch gleich
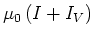 sein muss. Gemäss dem Ergebnis in 7d ist das
sein muss. Gemäss dem Ergebnis in 7d ist das
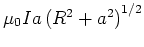 . Damit wird
. Damit wird
in Übereinstimmung
mit dem Resultat in Teil 7a, das wir nach dem Biot-Savart-Gesetz erhielten.
Übungsblatt 07
PHYS3100 Grundkurs IIIb (Physik, Wirtschaftsphysik, Physik Lehramt)
This document was generated using the
LaTeX2HTML translator Version 99.2beta8 (1.46)
Copyright © 1993, 1994, 1995, 1996,
Nikos Drakos,
Computer Based Learning Unit, University of Leeds.
Copyright © 1997, 1998, 1999,
Ross Moore,
Mathematics Department, Macquarie University, Sydney.
The command line arguments were:
latex2html uebungsblatt07
The translation was initiated by marti on 2004-02-10


Up: PHYS3100 Grundkurs IIIb
Othmar Marti
Experimentelle Physik
Universiät Ulm
![\includegraphics[width=0.45\textwidth]{ue-04-07-01.eps}](img2.gif)
![\includegraphics[width=0.6\textwidth]{ue-04-07-02.eps}](img3.gif)
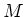
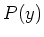 auf der (raumfesten)
auf der (raumfesten)
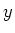 -Achse, wobei
-Achse, wobei 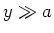 ist.
ist.
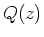 auf der (raumfesten)
auf der (raumfesten)
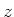 -Achse, wobei
-Achse, wobei 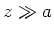 ist.
ist.
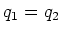 ist.
ist.
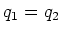 ist.
ist.
![\includegraphics[width=0.4\textwidth]{nachklausur-03.eps}](img38.gif)
 ohne äusseres Feld
auf.
ohne äusseres Feld
auf.
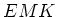 wirkt.
Schreiben Sie dazu das anregende Feld
wirkt.
Schreiben Sie dazu das anregende Feld
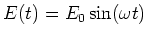 als komplexe Funktion, aber so, dass
der Realteil dieser Funktion gerade der gegebenen reellen Anregung entspricht.
als komplexe Funktion, aber so, dass
der Realteil dieser Funktion gerade der gegebenen reellen Anregung entspricht.
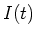 um.
um.
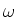 der Anregung den komplexen Strom
der Anregung den komplexen Strom
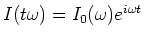 .
.
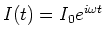 ist (ohne einsetzen), und dieser Strom durch den Widerstand
ist (ohne einsetzen), und dieser Strom durch den Widerstand 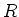 fliesst, was ist dann
die über eine Anzahl
fliesst, was ist dann
die über eine Anzahl
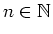 gemittelte thermische Leistung an
gemittelte thermische Leistung an 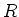 ?
?
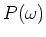 , die als Joulsche
Wärme im Widerstand
, die als Joulsche
Wärme im Widerstand 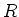 deponiert wird.
deponiert wird.
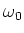 des Schwingkreises?
des Schwingkreises?
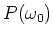 ?
?
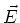 -Feld im Inneren des Plattenkondensators für ein stationäres
äusseres
-Feld im Inneren des Plattenkondensators für ein stationäres
äusseres 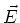 -Feld
-Feld 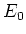 .
.
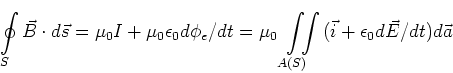
![\includegraphics[width=0.53\textwidth]{ue-07-01.eps}](img51.gif)
![]() und
und ![]() befinden sich im Abstand
befinden sich im Abstand ![]() vom Nullpunkt auf der
vom Nullpunkt auf der ![]() -Achse bei
-Achse bei ![]() und
und ![]() . Entlang der Verbindungslinie fliesst ein Strom
. Entlang der Verbindungslinie fliesst ein Strom ![]() . Der Punkt
. Der Punkt ![]() befindet sich
auf der
befindet sich
auf der ![]() -Achse im Abstand
-Achse im Abstand ![]() .
.
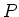 durch
durch
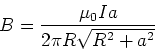
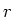 und der Breite
und der Breite 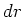 liege in der
liege in der 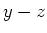 -Ebene. Zeigen Sie, dass der Fluss des elektrischen Feldes durch diesen Streifen
durch
-Ebene. Zeigen Sie, dass der Fluss des elektrischen Feldes durch diesen Streifen
durch
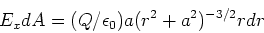
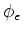 durch die
kreisförmige Ebene mit dem Radius
durch die
kreisförmige Ebene mit dem Radius 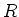 . Es ergibt sich
. Es ergibt sich
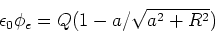
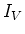 und zeigen Sie, dass
und zeigen Sie, dass
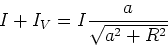
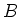 das gleiche Ergebnis erhält.
das gleiche Ergebnis erhält.
![\begin{displaymath}I_{C_1}=I_{C_2}+I_{C_2}\frac{R+X_{C_2}}{X_L}=I_{C_2}\left[1+\frac{R+X_{C_2}}{X_L}\right]\end{displaymath}](img74.gif)
![\begin{displaymath}U_0 = I_{C_2}\left[1+\frac{R+X_{C_2}}{X_L}\right]\cdot X_{C_1}+I_{C_2}\left({R+X_{C_2}}\right)\end{displaymath}](img75.gif)
![\begin{displaymath}I_{C_2} = \frac{U_0\cdot X_L}{\left[X_L+\left(R+X_{C_2}\right)\right]\cdot X_{C_1}+X_L\left({R+X_{C_2}}\right)}\end{displaymath}](img77.gif)
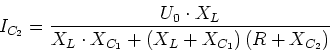
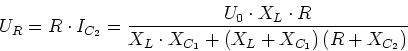
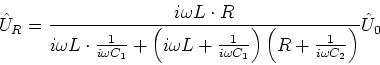
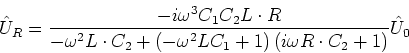
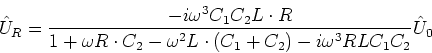
![\includegraphics[width=0.6\textwidth]{ue-04-07-03.eps}](img86.gif)
![\includegraphics[width=0.6\textwidth]{ue-04-07-04.eps}](img87.gif)
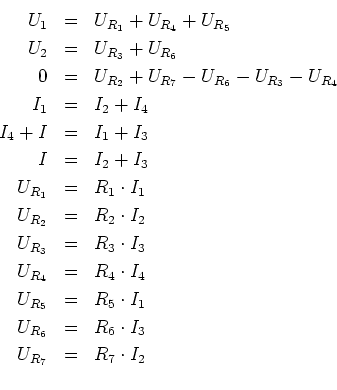
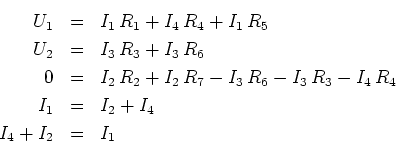
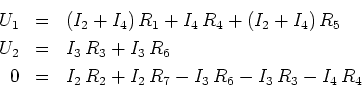
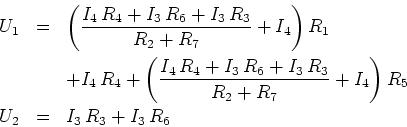
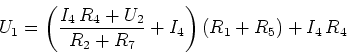
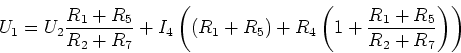
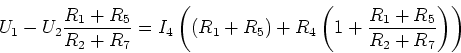
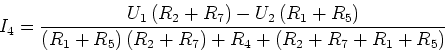
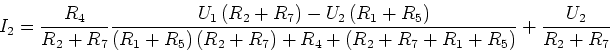
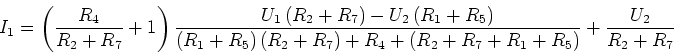
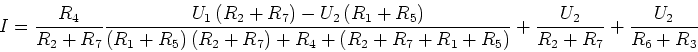
![\begin{displaymath}U_{R1}=R_1\left[\left(\frac {R_4}{R_2+R_7}+1\right)
\frac{U_...
...+R_4+\left(R_2+R_7+R_1+R_5\right)}
+\frac{U_2}{R_2+R_7}\right]\end{displaymath}](img106.gif)
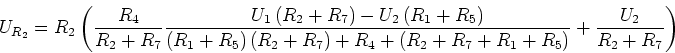
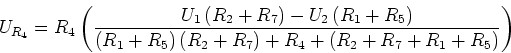
![\begin{displaymath}U_{R_5} = R_5\left[\left(\frac {R_4}{R_2+R_7}+1\right)
\frac...
...+R_4+\left(R_2+R_7+R_1+R_5\right)}
+\frac{U_2}{R_2+R_7}\right]\end{displaymath}](img110.gif)
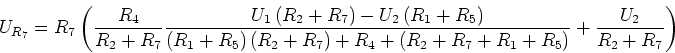
![\includegraphics[width=0.6\textwidth]{ue-04-07-05.eps}](img128.gif)
![\includegraphics[width=0.6\textwidth]{ue-04-07-06.eps}](img134.gif)
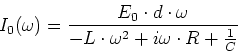
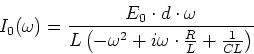
![\begin{displaymath}P(t) = R\cdot \left[\mathcal{R}e \left(I(t)\right)\right]^2 =...
...) = {R I_0^2}\left(\frac{1}{2}+\frac{\cos(2\omega t)}{2}\right)\end{displaymath}](img159.gif)
![\begin{eqnarray*}\left<P(\omega)\right>_{nT} &=& \frac{R}{2} I_0(\omega) \overli...
...}{CL}-\omega^2\right)^2
+\omega^2\cdot \frac{R^2}{L^2}\right]}
\end{eqnarray*}](img161.gif)
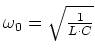
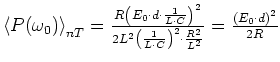
![\includegraphics[width=0.5\textwidth]{ue-07-02.eps}](img166.gif)
![\includegraphics[width=0.5\textwidth]{ue-07-03.eps}](img169.gif)
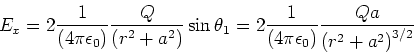
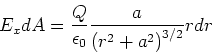
![\begin{eqnarray*}
\phi_{e} & =& {\displaystyle\int\nolimits_{0}^{R}}E_{x}2\pi r...
...[ \frac{1}{\left( R^{2}+a^{2}\right) ^{1/2}}+\frac{1}{a}\right]
\end{eqnarray*}](img176.gif)
![\begin{displaymath}\epsilon_{0}\phi_{e}=Q\left[ 1-\frac{a}{\left( R^{2}+a^{2}\right) ^{1/2}}\right] \end{displaymath}](img177.gif)
![$I_{V}=-I\left[ 1-a/\left(R^{2}+a^{2}\right) ^{1/2}\right] $](img181.gif) und
und