Weiter: Das Ohmsche Gesetz Oben: Elektrische Ströme Zurück: Elektrische Ströme Skript: PDF-Datei Übungen: Blätter
(Siehe Leisi, Klassische Physik II [Lei98, pp. 64])
![\includegraphics[width=0.7\textwidth]{elektrostatik-025}](img652.gif)
Berechnung des Stromes in einem Medium
|
Wir betrachten Ladungsträger mit der einheitlichen Ladung ![]() . Die Ladungsträgerdichte
. Die Ladungsträgerdichte ![]() habe die Geschwindigkeit
habe die Geschwindigkeit
![]() .
.
Der Strom
![]() durch das Flächenelement
durch das Flächenelement ![]() ist
ist
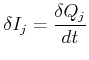 |
(3.136) |
| (3.137) |
und damit
| (3.138) |
Der gesamte Strom der Ladungsträger ![]() ist dann
ist dann
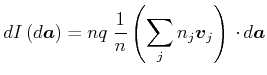 |
(3.139) |
wobei
![]() ist.
ist.
Die mittlere Geschwindigkeit der Ladungsträger ist
Wir definieren das Vektorfeld der Stromdichte
![]() ist abhängig vom Ort, da auch
ist abhängig vom Ort, da auch ![]() und
und
![]() ortsabhängig sind.
ortsabhängig sind.
| (3.142) |
und, integriert,
Diese Gleichung besagt, dass der Strom gleich dem Fluss des
Stromdichtefeldes durch eine Fläche ![]() ist.
ist.
Wird der Strom durch mehrere Arten von Ladungsträgern gebildet, schreibt man
Beispiel
Driftgeschwindigkeit in einem Kupferdraht mit ![]() Durchmesser und
Durchmesser und ![]()
Annahme: 1 Elektron pro Cu - Atom
Anzahl Cu - Atome pro Volumen
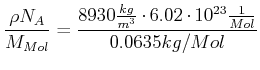 |
(3.145) | ||
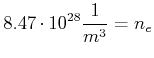 |
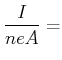 |
(3.146) | ||
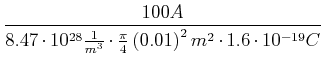 |
|||
Mit
![]() und
und
![]() hat man
hat man
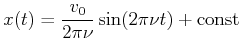
Folgerung: bei
![]() Wechselstrom zittern die Elektronen einige
Wechselstrom zittern die Elektronen einige
![]() weit.
weit.
![\includegraphics[width=0.6\textwidth]{elektrostatik-026}](img686.gif)
Berechnung des Flusses eines Stromdichtefeldes durch ein geschlossenes Gebiet
|
Wir betrachten eine geschlossene Fläche ![]() , die wir in zwei Teilflächen
, die wir in zwei Teilflächen ![]() und
und ![]() aufteilen, so dass auf der
Fläche
aufteilen, so dass auf der
Fläche ![]() die Feldlinie aus der Fläche austreten und auf der Fläche
die Feldlinie aus der Fläche austreten und auf der Fläche ![]() sie eindringen.
sie eindringen.
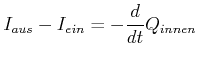 |
(3.147) |
Wir schreiben die Gleichung mit der Stromdichte um
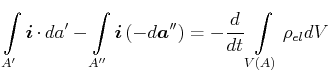 |
(3.148) |
oder
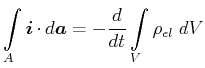 |
(3.149) |
Dies ist die Integralform der Kontinuitätsgleichung.
Mit dem Gaussschen Satz bekommen wir
Die Differentialform der Kontinuitätsgleichung lautet demnach:
Bei stationären Strömen hängen
![]() und
und ![]() nicht von der Zeit ab, so dass
nicht von der Zeit ab, so dass
ist.
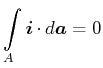 |
(3.153) |
Beispiel
![\includegraphics[width=0.6\textwidth]{elektrostatik-027}](img696.gif)
Stromfluss in einem Kondensator
|
Wir betrachten eine quasistationäre Änderung am Kondensator
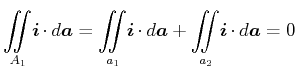 |
(3.154) |
Mit
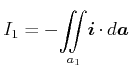 und
und
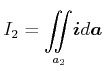 folgt
folgt
| (3.155) |
d.h. es scheint, als ob der Strom durch den Kondensator hindurch fliessen würde.
Wenn wir die Kontinuitätsgleichung auf ![]() anwenden, bekommen wir
anwenden, bekommen wir
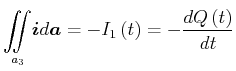 |
(3.156) |
oder
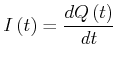 |
(3.157) |
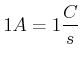 |
(3.158) |
Othmar Marti