Weiter: Poynting-Vektor und Energiefluss Oben: Elektromagnetische Wellen Zurück: Die Wellengleichung im Vakuum Skript: PDF-Datei Übungen: Blätter
Wir untersuchen die Wellenphänomene an 3 Testsystemen,
|
|
|
|
![\includegraphics[width=0.7\textwidth]{em-wellen-001}](img1506.gif)
Drei mögliche Doppelleitersysteme. Links die Lecherleitung, in der Mitte eine
Doppelleiterleitung, wie sie bei Printplatten üblich ist und rechts ein Koaxialkabel
|
Wenn man das Doppelleitersystem mit elektromagnetischen Wellen mit einer Wellenlänge von etwa
![]() speist, beobachtet man folgendes
speist, beobachtet man folgendes
![\includegraphics[width=0.4\textwidth]{em-wellen-002}](img1511.gif)
Magnetfelder und elektrische Felder bei einer Lecherleitung
|
![\includegraphics[width=0.7\textwidth]{em-wellen-003}](img1512.gif)
Magnetfelder und elektrische Felder bei einer Doppelleitung aus parallelen Platten
|
Wir setzen für die ![]() -Welle in der Geometrie der obigen Zeichnung an
-Welle in der Geometrie der obigen Zeichnung an
| (6.486) | |||
| (6.487) | |||
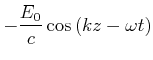 |
|||
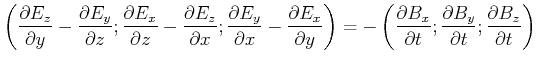 |
(6.488) |
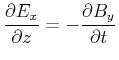 |
(6.489) |
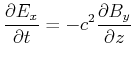 |
(6.490) |
![\includegraphics[width=0.7\textwidth]{em-wellen-004}](img1526.gif)
Ausbreitung von elektromagnetischen Wellen
|
Diese elektromagnetischen Wellen im Innenraum zwischen den beiden Leitern müssen auch in den angrenzenden Leitern Ladungswellen und Stromwellen erzeugen, die mit den Maxwellgleichungen kompatibel sind. Für die Ladungen gilt mit der ersten Maxwellschen Gleichung für die Oberflächenladungsdichte
| (6.491) |
![$\displaystyle b\cdot\left[j(z+dz,t)-j(z,t)\right]= -\frac{\partial \sigma(z,t)}{\partial t}\cdot b \cdot dz$](img1528.gif) |
(6.492) |
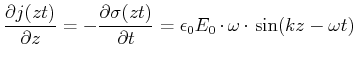 |
(6.493) |
| (6.494) |
![\includegraphics[width=0.5\textwidth]{em-wellen-005}](img1531.gif)
Integrationspfad zur Anwendung des vierten Maxwellschen Gesetzes
|
Mit dem vierten Maxwellschen Gesetz
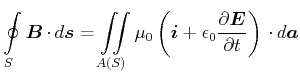 erhalten wir mit dem
eingezeichneten Integrationsweg, da der Term mit
erhalten wir mit dem
eingezeichneten Integrationsweg, da der Term mit ![]() keinen Beitrag gibt (er liegt in der Integrationsebene)
keinen Beitrag gibt (er liegt in der Integrationsebene)
| (6.495) |
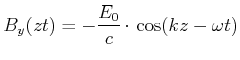 |
(6.496) |
An einer festen Stelle ![]() berechnen wir die E.M.K. zwischen den Leitern.
berechnen wir die E.M.K. zwischen den Leitern.
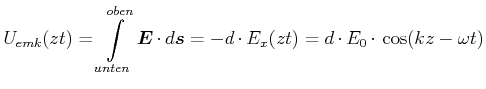 |
(6.497) |
| (6.498) |
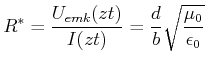 |
(6.499) |
Das Zweidraht-Doppelleitersystem hat den Wellenwiderstand
Stehende Wellen werden aus zwei fortlaufenden Wellen mit entgegengesetztem Wellenvektor ![]() zusammengesetzt.
Dabei müssen
zusammengesetzt.
Dabei müssen ![]() ,
, ![]() und
und ![]() in dieser Reihenfolge ein Rechtssystem bilden13. Die nach rechts laufende Welle wurde schon berechnet (hier sind nur die von
null verschiedenen Komponenten angegeben)
in dieser Reihenfolge ein Rechtssystem bilden13. Die nach rechts laufende Welle wurde schon berechnet (hier sind nur die von
null verschiedenen Komponenten angegeben)
| (6.502) | |||
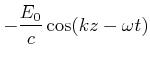 |
| (6.503) | |||
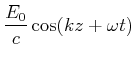 |
| (6.504) | |||
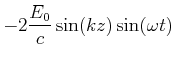 |
|
Im Gegensatz zu laufenden Wellen sind bei stehenden Wellen die Maxima der |
Othmar Marti