Vektoridentitäten

(Siehe Bronstein, Taschenbuch der Mathematik [BSMM00, pp. 190])

Im Folgenden sind $\vec{a}$, $\vec{b}$, $\vec{c}$ und $\vec{f}$ Vektoren oder vektorielle Funktionen, $a$, $b$, $c$ und $f$ ihre Längen, $k$ eine Zahl und $\varphi(\vec{r})$ eine skalare Funktion. Die Komponenten der Vektoren in kartesischen Koordinaten sind

$$\vec{a}= \left(\begin{array}{c} a_x \ a_y \ a_z \end{array}\right)$$

Für die anderen Vektoren werden die Komponenten analog geschrieben.

Produkte mit Vektoren

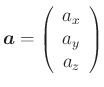
Skalarprodukt

$$k = \vec{a}\cdot \vec{b}= a_x b_x + a_y b_y + a_z b_z = a b \cos\left(\angle\left(\vec{a}\text{,} \vec{b}\right)\right)$$ (A..527)

Vektorprodukt

$$\vec{c}= \vec{a}\times \vec{b}= \left(\begin{array}{c}a_y b_z-a_z... ...right\vert = a b \sin\left(\angle\left(\vec{a}\text{,} \vec{b}\right)\right)$$ (A..528)

Vertauschung der Reihenfolge (Kommutationsgesetze)

$$\vec{a}\cdot\vec{b} = \vec{b}\cdot \vec{a}$$ (A..529)

$$\vec{a}\times\vec{b} = -\vec{b}\times \vec{a}$$ (A..530)

Zwei Vektoren sind orthogonal, wenn

$$\vec{a}\cdot\vec{b}= 0$$ (A..531)

Sie sind kollinear, wenn

$$\vec{a}\times\vec{b}=\vec{0}$$ (A..532)

Doppeltes Vektorprodukt

$$\vec{a}\times\left(\vec{b}\times\vec{c}\right) = \left(\vec{a}\cdot\vec{c}\right)\vec{b}-\left(\vec{a}\cdot\vec{b}\right)\vec{c}$$ (A..533)

Spatprodukt oder gemischtes Produkt

$$\left(\vec{a}\times\vec{b}\right)\cdot \vec{c} = \left(\vec{b}\times\vec{c}\right)\cdot \vec{a}$$

$$= \left(\vec{c}\times\vec{a}\right)\cdot \vec{b}$$

$$= -\left(\vec{b}\times\vec{a}\right)\cdot \vec{c}$$

$$= -\left(\vec{c}\times\vec{b}\right)\cdot \vec{a}$$

$$= -\left(\vec{a}\times\vec{c}\right)\cdot \vec{b}$$

$$=a_x b_y c_z + a_y b_z c_x + a_z b_x c_y -\left(a_z b_y c_x + a_x b_z c_y + a_y b_x c_z\right)$$ (A..534)

Drei Vektoren sind komplanar, wenn

$$\left(\vec{a}\times\vec{b}\right)\cdot \vec{c}= 0$$ (A..535)

Lagrangesche Identität

$$\left(\vec{a}\times\vec{b}\right)\cdot\left(\vec{c}\times\vec{f}\... ...vec{f}\right)- \left(\vec{a}\cdot\vec{f}\right)\left(\vec{b}\cdot\vec{c}\right)$$ (A..536)

Vierfaches Vektorprodukt

$$\left(\vec{a}\times\vec{b}\right)\times\left(\vec{c}\times\vec{d}... ...ight)\vec{c}- \left(\left(\vec{a}\times\vec{b}\right)\cdot\vec{c}\right)\vec{f}$$ (A..537)

Ableiten von Vektoren

Ableiten eines Vektors

$$\frac{d}{dt}\vec{a}= \frac{d}{dt}\left(\begin{array}{c}a_x\ a_y... ...t)= \left(\begin{array}{c}\dot{a_x}\ \dot{a_y}\ \dot{a_z}\end{array}\right)$$ (A..538)

Ableitung eines Produktes

$$\frac{d}{d t}\left(\varphi(t) \vec{a}(t)\right) = \frac{d \varphi}{d t}\vec{a}+\varphi\frac{d}{d t}\vec{a}$$ (A..539)

Ableitung des Skalarproduktes

$$\frac{d}{d t} \left(\vec{a}\cdot \vec{b}\right) = \frac{ d\vec{a}}{d t}\cdot \vec{b}+ \vec{a}\cdot \frac{d \vec{b}}{d t}$$ (A..540)

Ableitung des Vektorproduktes

$$\frac{d}{d t} \left(\vec{a}\times \vec{b}\right) = \frac{ d\vec{a}}{d t}\times \vec{b}+ \vec{a}\times \frac{d \vec{b}}{d t}$$ (A..541)

Ableitung eines Vektors mit konstantem Betrag. Hier ist $\vec{a}\cdot\vec{a}= a^2 = const$. Aus Gleichung (A.14) folgt

$$0 = \frac{d a^2}{d t} = \frac{d}{d t}\left(\vec{a}\cdot \vec{a}\r... ...}}{d t}\cdot \vec{a}\qquad \Rightarrow\qquad \frac{d \vec{a}}{d t} \bot \vec{a}$$ (A..542)

Taylorentwicklung einer Vektorfunktion

$$\vec{a}(t+\tau)=\vec{a}(t)+ \tau\left.\frac{d \vec{a}}{d t}\right... ...+ \ldots +\frac{\tau^n}{n!}\left.\frac{d^n \vec{a}}{d t^n}\right\vert _t+\ldots$$ (A..543)

Vektorableitungen bei Skalarfeldern

Ableitung eines skalaren Feldes nach einer Richtung

$$\frac{\partial \varphi(\vec{r})}{\partial \vec{c}} = \lim\limits_... ...ow 0} \frac{\varphi(\vec{r}+\varepsilon\vec{c}) -\varphi(\vec{r})}{\varepsilon}$$ (A..544)

Ableitung $\frac{\partial \varphi(\vec{r})}{\partial \vec{e}_{\vec{c}}}$ in Richtung des Einheitsvektors $\vec{e}_{\vec{c}}$ in Richtung von $\vec{c}$

$$\frac{\partial \varphi(\vec{r}}{\partial \vec{c}} = \left\vert\vec{c}\right\vert\frac{\partial \varphi(\vec{r})}{\partial \vec{e}_{\vec{c}}}$$ (A..545)

Richtungsableitung einer skalaren Funktion im Vergleich zur Richtung mit dem stärksten Abfall (Einheitsvektor $\vec{n}$)

$$\frac{\partial \varphi(\vec{r})}{\partial \vec{e}_{\vec{c}}} = \f... ...})}{\partial \vec{n}} \cos\left(\angle \vec{e}{\vec{c}}\text{,} \vec{n}\right)$$ (A..546)

Vektorableitungen bei Vektorfeldern

Ableitung eines Vektorfeldes $\vec{a}$ nach einer Richtung

$$\frac{\partial \vec{a}(\vec{r})}{\partial \vec{c}} = \lim\limits_... ...ow 0} \frac{\vec{a}(\vec{r}+\varepsilon\vec{c}) -\vec{a}(\vec{r})}{\varepsilon}$$ (A..547)

Ableitung $\frac{\partial \vec{a}(\vec{r})}{\partial \vec{e}_{\vec{c}}}$ in Richtung des Einheitsvektors $\vec{e}_{\vec{c}}$ in Richtung von $\vec{c}$

$$\frac{\partial \vec{a}(\vec{r}}{\partial \vec{c}} = \left\vert\vec{c}\right\vert\frac{\partial \vec{a}(\vec{r})}{\partial \vec{e}_{\vec{c}}}$$ (A..548)

Richtungsableitung einer Vektorfunktion

$$\frac{\partial \vec{a}(\vec{r})}{\partial \vec{c}} = \left(\vec{c}\cdot {}\boldsymbol{\mathrm{grad}}{} \right)\vec{a}$$ (A..549)

$$= \frac{1}{2}\left[ {}\boldsymbol{\mathrm{rot}}{} \left(\vec{a}\t... ...\cdot\vec{a}\right) +\vec{c}\cdot {}\boldsymbol{\mathrm{div}}{} \vec{a}\right.$$

$$\left.-\vec{a}\cdot {}\boldsymbol{\mathrm{div}}{} \vec{c}-\vec{c... ...hrm{rot}}{} \vec{a}-\vec{a}\times {}\boldsymbol{\mathrm{rot}}{} \vec{c}\right]$$

Gradient eines Produktes

$${}\boldsymbol{\mathrm{grad}}{} \left(\varphi_1 \varphi_2\right)... ...mathrm{grad}}{} \varphi_2 + \varphi_2 {}\boldsymbol{\mathrm{grad}}{} \varphi_1$$ (A..550)

Kettenregel beim Gradienten

$${}\boldsymbol{\mathrm{grad}}{} \varphi_1\left(\varphi_2\right) = \frac{d \varphi_1}{d \varphi_2} {}\boldsymbol{\mathrm{grad}}{} \varphi_2$$ (A..551)

Gradient eines Skalarproduktes

$${}\boldsymbol{\mathrm{grad}}{} \left(\vec{a}\cdot\vec{b}\right)... ...ol{\mathrm{rot}}{} \vec{b}+\vec{b}\times {}\boldsymbol{\mathrm{rot}}{} \vec{a}$$ (A..552)

Gradient eines Skalarproduktes eines konstanten Vektors $\vec{k}$ mit einem Ortsvektor $\vec{r}$

$${}\boldsymbol{\mathrm{grad}}{} \left(\vec{r}\cdot \vec{k}\right) = \vec{k}$$ (A..553)

Divergenz eines Produktes

$${}\boldsymbol{\mathrm{div}}{} \left(\varphi \vec{a}\right) = \v... ...dsymbol{\mathrm{div}}{} \vec{a}+\vec{a} {}\boldsymbol{\mathrm{grad}}{} \varphi$$ (A..554)

Divergenz eines Skalarproduktes eines konstanten Vektors $\vec{k}$ mit einem Ortsvektor $\vec{r}$

$${}\boldsymbol{\mathrm{div}}{} \left(\vec{r}\cdot\vec{k}\right) = \frac{\vec{r}\cdot\vec{k}}{\left\vert\vec{r}\right\vert}$$ (A..555)

Divergenz eines Vektorproduktes

$${}\boldsymbol{\mathrm{div}}{} \left(\vec{a}\times\vec{b}\right)... ...bol{\mathrm{rot}}{} \vec{a}-\vec{a}\cdot {}\boldsymbol{\mathrm{rot}}{} \vec{b}$$ (A..556)

Rotation eines Produktes

$${}\boldsymbol{\mathrm{rot}}{} \left(\varphi \vec{a}\right) = \v... ...\mathrm{rot}}{} \vec{a}+ {}\boldsymbol{\mathrm{grad}}{} \varphi \times \vec{a}$$ (A..557)

Rotation eines Vektorproduktes

$${}\boldsymbol{\mathrm{rot}}{} \left(\vec{a}\times\vec{b}\right)... ...ldsymbol{\mathrm{div}}{} \vec{b}-\vec{b} {}\boldsymbol{\mathrm{div}}{} \vec{a}$$ (A..558)

Rotation eines Potentialfeldes

$${}\boldsymbol{\mathrm{rot}}{} \left( {}\boldsymbol{\mathrm{grad}}{} \varphi\right)=\vec{0}\qquad \forall \varphi$$ (A..559)

Divergenz einer Rotation

$${}\boldsymbol{\mathrm{div}}{} \left( {}\boldsymbol{\mathrm{rot}}{} \vec{a}\right)= 0 \qquad \forall \vec{a}$$ (A..560)

Rotation einer Rotation

$${}\boldsymbol{\mathrm{rot}}{} \left( {}\boldsymbol{\mathrm{rot... ...oldsymbol{\mathrm{div}}{} \left( {}\boldsymbol{\mathrm{grad}}{} \vec{a}\right)$$ (A..561)

Totale Ableitung bei mitgeführten Koordinatensystemen

Wenn $\vec{v}=\frac{d}{d t}\vec{r}$ ein konstanter Geschwindigkeitsvektor ist und diese Grösse an einem mit der Geschwindigkeit $\vec{v}$ bewegten Ort beobachtet wird, dann gilt (Siehe Jackson[Jac75, p212]):

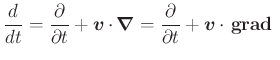$$\frac{d}{d t} = \frac{\partial}{\partial t} + \vec{v}\cdot \vec{\... ...}= \frac{\partial}{\partial t} + \vec{v}\cdot {}\boldsymbol{\mathrm{grad}}{}$$ (A..562)

wobei $\frac{d}{d t}$ die totale Ableitung im raumfesten Koordinatensystem und $\frac{\partial}{\partial t}$ die lokale, mitgeführte Ableitung ist. Mit Gleichung (A.32) kann man schreiben

$${}\boldsymbol{\mathrm{rot}}{} \left(\vec{B}\times\vec{v}\right) = \left(\vec{v}\cdot {}\boldsymbol{\mathrm{grad}}{} \right)\vec{... ...ldsymbol{\mathrm{div}}{} \vec{v}-\vec{v} {}\boldsymbol{\mathrm{div}}{} \vec{B}$$

$$\vec{\nabla}\times\left(\vec{B}\times\vec{v}\right) = \left(\vec{v}\cdot\vec{\nabla}\right)\vec{B}- \left(\vec{B}\cdo... ...\right)\vec{v}+\vec{B}\vec{\nabla}\cdot \vec{v}-\vec{v}\vec{\nabla}\cdot\vec{B}$$ (A..563)

oder

$$\left(\vec{v}\cdot {}\boldsymbol{\mathrm{grad}}{} \right)\vec{B} = {}\boldsymbol{\mathrm{rot}}{} \left(\vec{B}\times\vec{v}\righ... ...ldsymbol{\mathrm{div}}{} \vec{v}+\vec{v} {}\boldsymbol{\mathrm{div}}{} \vec{B}$$

$$\left(\vec{v}\cdot\vec{\nabla}\right)\vec{B} = \vec{\nabla}\times\left(\vec{B}\times\vec{v}\right) + \left(\ve... ...\right)\vec{v}-\vec{B}\vec{\nabla}\cdot \vec{v}+\vec{v}\vec{\nabla}\cdot\vec{B}$$ (A..564)

Nun ist ${}\boldsymbol{\mathrm{div}}{} {\vec{B}}=0$. Weiter ist ${}\boldsymbol{\mathrm{div}}{} \left(\frac{d}{d t} \vec{v}\right) = \frac{d}{d t} {}\boldsymbol{\mathrm{div}}{} \vec{v}= \frac{d}{d t} (3) = 0$ und ${}\boldsymbol{\mathrm{grad}}{} \vec{v}= \frac{d}{dt} {}\boldsymbol{\mathrm{grad}}{} \vec{r}= \frac{d}{d t} E = 0$, wobei $E$ die 3 mal 3 Einheits-Diagonalmatrix ist. Damit haben wir ohne Einschränkung der Allgemeinheit

$$\left(\vec{v}\cdot {}\boldsymbol{\mathrm{grad}}{} \right)\vec{B} = {}\boldsymbol{\mathrm{rot}}{} \left(\vec{B}\times\vec{v}\right)$$

$$\left(\vec{v}\cdot\vec{\nabla}\right)\vec{B} = \vec{\nabla}\times\left(\vec{B}\times\vec{v}\right)$$ (A..565)

und

$$\frac{d}{d t}\vec{B}= \frac{\partial}{\partial t}\vec{B}+ \vec{v}... ...artial}{\partial t}\vec{B}+ \vec{\nabla}\times\left(\vec{B}\times\vec{v}\right)$$ (A..566)