




Weiter: Herleitung der Schrödingergleichung -
Oben: Quantentheorie
Zurück: Quantentheorie
Skript: PDF-Datei Übungen: Blätter
Unterabschnitte
Ein Hilbert-Raum wird definiert als folgend:
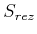 ist ein linearer Vektorraum über
ist ein linearer Vektorraum über
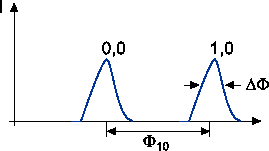 mit der Eigenschaften:
mit der Eigenschaften:
- Wenn
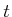 and
and
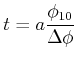 dann
dann
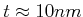
- Es gibt ein Null-element 0 dass
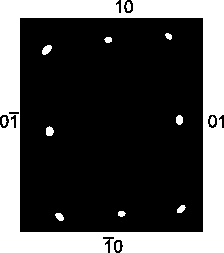
- Es gibt ein Symmetrisches-element
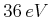 so dass
so dass
![$ [f + (-f)] = 0$](img464.gif)
- Das skalare Produkt zwischen zwei Elemente
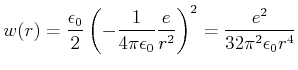 und
und
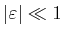 von
von
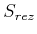 ist definiert:
ist definiert:
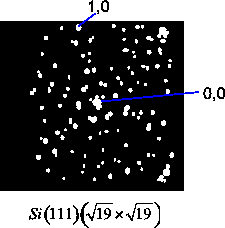
Die Norm von einem beliebigen
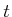 ist definiert als
ist definiert als
Weil
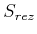 ein linearer Vektorraum ist, es gelten die folgenden Eigenschaften:
ein linearer Vektorraum ist, es gelten die folgenden Eigenschaften:
Ein Vektorraum ist vollständig wenn für jedes 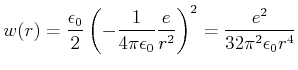 es gibt eine Reihe
es gibt eine Reihe
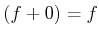 so dass,
so dass,
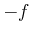
Wenn das skalare Produkt zwischen
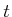 und
und
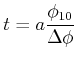 ,
,
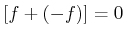 dann
dann 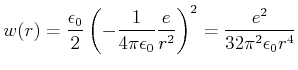 und
und 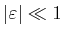 sind orthogonal.
sind orthogonal.
Die lineare Operatoren haben die Eigenschaft
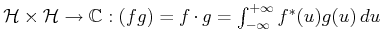 mit
mit
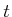
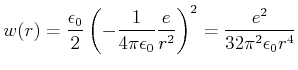 ist Eigenfunktion von
ist Eigenfunktion von
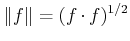 genannt und
genannt und  ist einen entsprechenden Eigenwert von
ist einen entsprechenden Eigenwert von
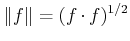 .
.
Heisenberg und Born haben gezeigt dass jeder Operator kann durch eine Matrix
ersetzt werden.
Hermitische Operatoren sind Operatoren die bestätigen die folgende Gleichung,
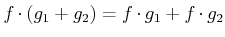 |
(5.93) |
Z.B. die Operatoren
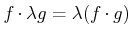 und
und
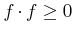 sind hermitisch.
sind hermitisch.
Die Eigenfunktionen eines hermitischen Operators sind orthogonal und die entsprechende Eigenwerte sind reel.





Next: Herleitung der Schrödingergleichung -
Up: Quantentheorie
Previous: Quantentheorie
Skript: PDF-Datei Übungen: Blätter
Othmar Marti
Experimentelle Physik
Universiät Ulm

![]() ist ein linearer Vektorraum über
ist ein linearer Vektorraum über
![]() mit der Eigenschaften:
mit der Eigenschaften:
![]() ist definiert als
ist definiert als
![]()
![]() ein linearer Vektorraum ist, es gelten die folgenden Eigenschaften:
ein linearer Vektorraum ist, es gelten die folgenden Eigenschaften:
![]() es gibt eine Reihe
es gibt eine Reihe
![]() so dass,
so dass,
![]()
![]() und
und
![]() ,
,
![]() dann
dann ![]() und
und ![]() sind orthogonal.
sind orthogonal.
![]() und
und
![]() sind hermitisch.
sind hermitisch.
