




Weiter: Herleitung der Schrödingergleichung -
Oben: Quantentheorie
Zurück: Hilbert-Räume
Skript: PDF-Datei Übungen: Blätter
Eine der Methoden um die Schrödinger Gleichung abzuleiten benutzt den Ansatz
![$ \psi(x) = A \exp[ i (k x - \omega t)
]$](img480.gif) und die de Broglie Relation
und die de Broglie Relation
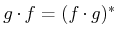 . Die erste und die zweite Ableitungen lauten,
. Die erste und die zweite Ableitungen lauten,
![$\displaystyle \frac{\partial \psi}{\partial x} = i k A \exp[ i (k x - \omega t) ] = i k \psi$](img482.gif) |
(5.94) |
bzw.
![$\displaystyle \frac{\partial^{2} \psi}{\partial x^{2}} = (i k)^{2} A \exp[ i (k x - \omega t) ] = -k^{2} \psi$](img483.gif) |
(5.95) |
Das Hamiltonsche Extremalprinzip sagt dass die Wirkung eines Systems stationär ist, d.h.
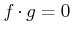 |
(5.96) |
Die Hamilton-Funktion ist dann definiert als die Summe zwischen der kinetischen und der potentiellen Energie:
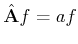 |
(5.97) |
 ist eine Funktion von
ist eine Funktion von 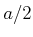 und
und
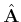 , wobei
, wobei  der Impuls eines punktförmigen Teilchens mit
Masse
der Impuls eines punktförmigen Teilchens mit
Masse 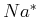 ist. Wir wissen nach Planck dass die Energie einer Welle quantisiert ist:
ist. Wir wissen nach Planck dass die Energie einer Welle quantisiert ist:
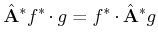 .
Gleichzeitig ihr Impuls ist
.
Gleichzeitig ihr Impuls ist
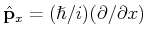 . Wenn ein Teilchen mit Masse
. Wenn ein Teilchen mit Masse 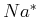 sich bewegt und eine Wellenlänge
sich bewegt und eine Wellenlänge
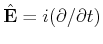 hat, wir können die obigen Gleichungen schreiben wie es folgt
hat, wir können die obigen Gleichungen schreiben wie es folgt
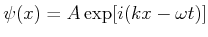 |
(5.98) |
bzw.
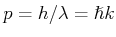 |
(5.99) |
Wir können dann die Operatoren Impuls
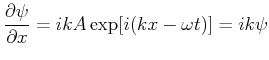 , und kinetische
Energie
, und kinetische
Energie
![$ \hat{\mathbf{T}}_{x} = - [\hslash^{2} / ( 2 m )]\partial^{2} / \partial x^{2}$](img493.gif) definieren.
definieren.
Die erste Ableitung von 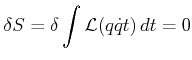 in der Zeit
in der Zeit 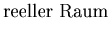 ist
ist
![$\displaystyle \frac{\partial \psi}{\partial t} = - i \omega A \exp[ i (k x - \omega t) ] = - i \omega \psi$](img495.gif) |
(5.100) |
Wir können also der Operator der gesamten Energie 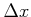 definieren:
definieren:
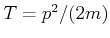 Wenn
Wenn 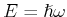 eine Konstante ist können wir ein Quantum-Operator für die Hamilton-Funktion definieren:
eine Konstante ist können wir ein Quantum-Operator für die Hamilton-Funktion definieren:
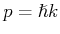 |
(5.101) |
Die Schrödingergleichung (SG) ist dann das Analogon zu der klassischen Hamilton-Funktion 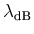 :
:
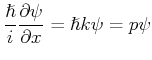 |
(5.102) |
Wir haben in dieser Ableitung die potentielle Energie als Konstante angenommen. Die Frage ist jetzt welche andere
Lösungen die Schrödinger-Gleichung haben kann, ausser die harmonische Wellenfunktion.
Wenn
![$ \psi(x) = A \exp[ i (k x - \omega t) ] = A \exp( i k x ) \exp( -i \omega t )$](img501.gif) d.h. wenn wir betrachten die
Wellenfunktion als eine stationäre Funktion mit harmonischer Zeitabhängigkeit wir können auch dir zeitunabhängige
Schrödinger Gleichung ableiten:
d.h. wenn wir betrachten die
Wellenfunktion als eine stationäre Funktion mit harmonischer Zeitabhängigkeit wir können auch dir zeitunabhängige
Schrödinger Gleichung ableiten:
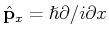 |
(5.103) |





Next: Herleitung der Schrödingergleichung -
Up: Quantentheorie
Previous: Hilbert-Räume
Skript: PDF-Datei Übungen: Blätter
Othmar Marti
Experimentelle Physik
Universiät Ulm
![$\displaystyle \frac{\partial \psi}{\partial x} = i k A \exp[ i (k x - \omega t) ] = i k \psi$](img482.gif)

![$\displaystyle \frac{\partial \psi}{\partial x} = i k A \exp[ i (k x - \omega t) ] = i k \psi$](img482.gif)
![$\displaystyle \frac{\partial^{2} \psi}{\partial x^{2}} = (i k)^{2} A \exp[ i (k x - \omega t) ] = -k^{2} \psi$](img483.gif)
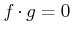
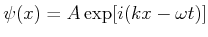
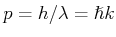
![]() , und kinetische
Energie
, und kinetische
Energie
![]() definieren.
definieren.
![]() in der Zeit
in der Zeit ![]() ist
ist
![$\displaystyle \frac{\partial \psi}{\partial t} = - i \omega A \exp[ i (k x - \omega t) ] = - i \omega \psi$](img495.gif)
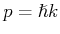
![]() :
:
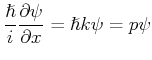
![]() d.h. wenn wir betrachten die
Wellenfunktion als eine stationäre Funktion mit harmonischer Zeitabhängigkeit wir können auch dir zeitunabhängige
Schrödinger Gleichung ableiten:
d.h. wenn wir betrachten die
Wellenfunktion als eine stationäre Funktion mit harmonischer Zeitabhängigkeit wir können auch dir zeitunabhängige
Schrödinger Gleichung ableiten:
