
optisches Spektrum: Balmer-Serie 1885
![]() Balmer:
Balmer:
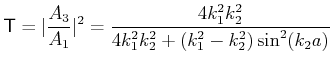 , , |
(6.200) |
mit ![]() .
.
andere Schreibweise
mit
![]()
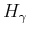 |
(6.201) |
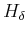 |
(6.202) |
mit
![]()
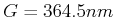 |
|||
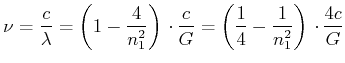 |
|||
![]() Seriengrenze bei
Seriengrenze bei
![]()
Die Differenzfrequenz zweier Linien aus einer Serie ist wieder eine beobachtete Linie im Spektrum.
![\includegraphics[width=0.7\textwidth]{balmer}](img730.gif)
Wellenlängen der Lyman, Balmer und Paschen-Serien im Wasserstoffspektrum.
|
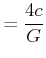 |
(6.203) |
![]() Elektronen in
Elektronen in ![]() haben diskrete Energieniveaux
haben diskrete Energieniveaux
Bohrsches Modell
Elektronen bewegen sich auf Planetenbahnen
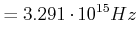 Kräftegleichgewicht Kräftegleichgewicht |
(6.204) |
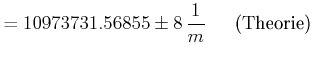 |
|||
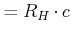 |
aus
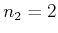 |
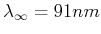 |
||
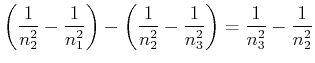 |
|||
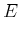 |
|||
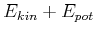 |
![$\displaystyle \sqrt[3]{\frac{4\pi\epsilon_{0}m_{0}\omega^{2}
}{e^{2}}}=\frac{\l...
...i\epsilon_{0}m_{0}\right) ^{\frac{1}{3}}
\omega^{\frac{2}{3}}}{e^{\frac{2}{3}}}$](img745.gif) |
||
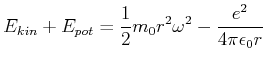 |
|||
![$\displaystyle -\frac{e^{\frac{4}{3}}\omega^{\frac{2}{3}}m_{0}^{\frac{1}{3}}}{24...
...ac{2}{3}}}=\sqrt[3]{\frac{e^{4}
\omega^{2}m_{0}}{2^{7}\pi^{2}\epsilon_{0}^{2}}}$](img748.gif) |
Problem: klassisch:
Bohrs Postulate:
mit
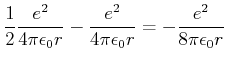 |
(6.205) |
folgt
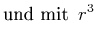 |
(6.206) |
Bohr: Umlauffrequenz = emittierte Frequenz
Dies stimmt bei kleinem ![]() nicht.
nicht.
Korrespondenzprinzip: für grosse ![]() muss die Quantenmechanik in die klassische Mechanik übergehen.
muss die Quantenmechanik in die klassische Mechanik übergehen.
Anwendung
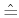 |
|||
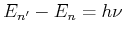 |
|||
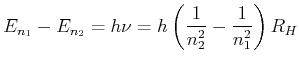 |
|||
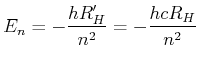 |
|||
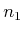 |
|||
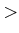 |
mit ![]() ist
ist
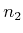 |
(6.207) |
und damit:
![$\displaystyle E=\frac{R_{H}hc}{n^{2}}=\sqrt[3]{\frac{e^{4}\omega^{2}m_{0}} {2^{...
...2^{7}\pi ^{2}\epsilon_{0}^{2}}\left( \frac{4\pi R_{H}c}{n_{1}^{3}}\right) ^{2}}$](img767.gif) |
(6.208) |
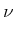 |
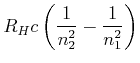 |
||
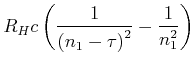 |
|||
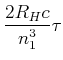 |
Radius der n-ten Bahn
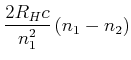 |
(6.209) |
Bahndrehimpuls
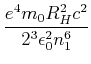 |
|||
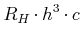 |
|||
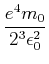 |
Fehler:
spektrale Grösse ![]() theoretische Grösse
theoretische Grösse
Grund: man muss mit der reduzierten Masse rechnen.
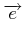 |
|||
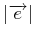 |
|||
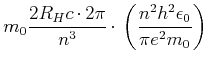 |
|||
Wasserstoffähnlich:
![]()
Myonium-Atom
![]()
