![\includegraphics[width=0.7\textwidth]{helium-terme}](img1594.gif)

Elektronenzustände in Atomen werden nach von tiefen Energien zu hohen besetzt.
![\includegraphics[width=0.7\textwidth]{helium-terme}](img1594.gif)
Termschema von Helium
|
| 1.Elektron |
|
|
|||
| 2.Elektron |
|
|
nach Anregung:
| 1.Elektron |
|
||||
| 2.Elektron |
|
Helium
![]() Spektrum
Spektrum
Singulett-System und Triplettsystem ohne Übergänge
![]() und
und ![]() sind metastabil
sind metastabil
![]() im Singulett-System
im Singulett-System
![]() Parahelium
Parahelium
![]() im Triplettsystem
im Triplettsystem
![]() Orthohelium
Orthohelium
Singulett: es wird keine Feinstruktur beobachtet, daraus folgt, dass die Spins der Elektronen antiparallel sind.
Bezeichnung: grosse Buchstaben bezeichnen gesamtes System
Gesamtspin ist
![]()
dessen magn. Moment ![]() hat drei Einstellmöglichkeiten
hat drei Einstellmöglichkeiten
| (6.431) |
Die Aufspaltung entsteht wegen der Spin-Bahn-Kopplung
Elektrostatische Wechselwirkung
![]() liegt über
liegt über
![]() der Abstand der Elektronen von der Spineinstellung abhängt.
der Abstand der Elektronen von der Spineinstellung abhängt.
Symmetrie-Energie
Elektronenenergie
![\begin{displaymath}\begin{array}[c]{cc} E=-\frac{Ze^{2}}{4\pi\epsilon_{0}r_{1}}-...
...silon_{0}r_{12}} & \overbrace{\text{Abstossung}} \end{array}\end{displaymath}](img1610.gif) |
(6.432) |
![]() Die potentielle Energie ist nicht mehr kugelsymmetrisch. Die Wellenfunktion kann nicht mehr
separiert werden.
Die potentielle Energie ist nicht mehr kugelsymmetrisch. Die Wellenfunktion kann nicht mehr
separiert werden.
Die Schrödingergleichung ist nicht geschlossen lösbar
![]() Störungsrechnung
Störungsrechnung
1. Näherung: vernachlässige die Abstossung
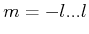 |
(6.433) |
Energien:
| (6.434) |
gemessen
![\begin{displaymath}\begin{array}[c]{ccc} E_{He}=-79eV & =-24,6eV & +-54,4eV &...
...{\text{1.Elektron}} & \overbrace{\text{2.Elektron}} \end{array}\end{displaymath}](img1613.gif) |
(6.435) |
Man könnte argumentieren, dass das äussere Elektron wegen der
Abschirmung die Kernladung ![]() sieht, und nicht
sieht, und nicht ![]() . Dann wäre aber
. Dann wäre aber
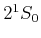 |
(6.436) | |
ein besserer Schätzwert, aber auch falsch.
Da ![]() aber nicht
aber nicht ![]() beobachtet wird, folgerte Wolfgang Pauli
beobachtet wird, folgerte Wolfgang Pauli
Die Elektronenzustände eines Atoms können mit Elektronen nur so besetzt werden,dass nie zwei oder mehr Elektronen in allen Quantenzahlen übereinstimmen.
wir haben die Bahndrehimpulse ![]()
Spins ![]()
Die Wechselwirkung
![]()
Wenn nun die Spin-Bahn-Kopplung
![]() klein ist gegen die Bahn-Bahnkopplung
klein ist gegen die Bahn-Bahnkopplung
![]() und gegen die Spin-Spin-Kopplung
und gegen die Spin-Spin-Kopplung
![]()
dann addieren alle
![\begin{displaymath}\begin{array}[c]{cc} \ell_{i} & \vec{L}=\sum\ell_{i} s_{i} & \vec{S}=\sum\vec{s}_{i} \end{array}\end{displaymath}](img1628.gif) |
(6.437) |
getrennt
und der Gesamtdrehimpuls ist
| (6.438) |
![]()
| Russel-Sauders-Kopplung |
Beträge
| (6.439) |
also ist
![]() mit
mit
![]()
![]() S-Term
S-Term
![]() P-Term
P-Term
![]() D-Term
D-Term
Auswahlregeln für optische Übergänge
Einzelektron
![]()
Gesamtsystem
![]()
Spin
| (6.440) | ||
Auswahlregel für Dipolstrahlung
| (6.441) |
![]() Terme mit verschiedenen Gesamtspin koppeln nicht
Terme mit verschiedenen Gesamtspin koppeln nicht
![]() Singulett, Triplett-System
Singulett, Triplett-System
Gesamtdrehimpuls
![]()
Welche Werte für ![]() sind möglich?
sind möglich?
![\begin{displaymath}
\begin{array}[c]{cc}
S=0 & J=L\\
S=\frac{1}{2} & J=L+\frac...
...rac{5}{2},L+\frac{1}{2},L-\frac{1}{2},L-\frac{3}{2}
\end{array}\end{displaymath}](img1647.gif)
![]() Terme
Terme
![]() : Grundzustand
: Grundzustand
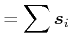
![]() für
für
![]()
Name
![]()
oder
![]() für
für
![]()
Name
![]() Dieser Zustand ist verboten (Pauli)
Dieser Zustand ist verboten (Pauli)
weiter
![]()
![]()
entweder ist
![]()
oder
![]()
beide,
![]() und
und
![]() sind errlaubt und werden beobachtet
sind errlaubt und werden beobachtet
Nomenklatur
![]()
Dabei ist ![]() die Hauptquantenzahl des höchsten angeregten Elektrons
die Hauptquantenzahl des höchsten angeregten Elektrons
| Anzahl Eltronen | 2 | 3 | 4 | 5 |
| Zustände |
|
|
||
| Singulett | Dublett | Singulett | Dublett | |
|
|
|
|||
| Triplett | Quartett | Triplett | Quartett | |
|
|
||||
| Quintett | Sextett |
bei schweren Atomen nimmt die Spin-Bahn-Kopplung mit der Kernladungszahl ![]() zu.
zu.
Dann koppeln zuerst Spin und Bahndrehimpuls
![]() und erst dann
und erst dann
| (6.442) |
die ![]() und
und ![]() sind nicht mehr definiert
sind nicht mehr definiert
| (6.443) |
Die ![]() -Kopplung zeigt sich am Auftreten von Interkombinationsfrequenzen. Sie tritt nur bei sehr
schweren Atomen auf.
-Kopplung zeigt sich am Auftreten von Interkombinationsfrequenzen. Sie tritt nur bei sehr
schweren Atomen auf.
Normenklatur
| (6.444) |
auch hier ist
| (6.445) |
Auswahlregeln:
| (6.446) |
wobei
![]() verboten ist.
verboten ist.
Das magnetische Moment bei ![]() -Kopplung ist
-Kopplung ist
| (6.447) |
![]() ist antiparallel zu
ist antiparallel zu ![]()
![]() ist antiparallel zu
ist antiparallel zu ![]()
da die ![]() -Faktoren jedoch unterschiedlich sind, ist
-Faktoren jedoch unterschiedlich sind, ist ![]() nicht antiparallel zu
nicht antiparallel zu
![]()
Das magnetische Moment
![]() präzediert um
präzediert um ![]()
Die Komponente
![]() von
von
![]() , die parallel zu
, die parallel zu ![]() ist.
ist.
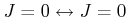 |
(6.448) |
mit
 |
(6.449) |
und
| (6.450) |
mit
![]()
