Weiter: Mehrelektronenatome Oben: Atome und ihr Aufbau Zurück: Atome im elektrischen Feld Skript: PDF-Datei Übungen: Blätter

Unterabschnitte

Drehsymmetrie

Auswahlregeln

Auswahlregeln:

$H_{1,2}^{s}$ sind ungleich null, alle anderen gleich null

$H_{1,2}^{s}=H_{2,1}^{s}=eE_{el}d$

wobei $E_{el}$ das elektrische Feld ist

mit N=4 ergibt sich

$\begin{displaymath}\begin{array}[c]{cc} \left( E_{2}^{0}-E\right) C_{1}+eE_{el}d... ..._{3}=0 & B \left( E_{2}^{0}-E\right) c_{4}=0 & B \end{array}\end{displaymath}$

(6.368)

aus folgt

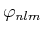$\displaystyle \begin{vmatrix}E_{2}^{0}-E & eE_{el}d eE_{el}d & E_{2}^{0}-E \end{vmatrix} =0$

(6.369)

und

$\displaystyle E_±$	$\displaystyle =E_{2}^{0}\pm eE_{el}d$	(6.370)
$\displaystyle +$	$\displaystyle :c_{1}=c_{2}$	(6.371)
$\displaystyle -$	$\displaystyle :c_{1}=-c_{2}$	(6.372)

aus folgt:

$\displaystyle E_{2}^{0}=E$

(6.373)

Dies wird nur bei H beobachtet, da nur bei H $\ell$ entartet ist.

Auswahlregeln

Zwischen zwei Wellenfunktionen ist das Übergangsmatrixelement für ein Dipolmoment in x-Richtung definiert (Dipolübergangsmatrixelement).

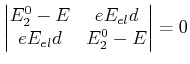$\displaystyle H_{mn}^{s}=\int\varphi_{m}^{\ast}\left( \vec{r}\right) ex\varphi_{n}\left( \vec{r}\right) dV$

(6.374)

Symmetrie von Wellenfunktionen

Beispiel: harmonischer Oszillator

Transformation $x\rightarrow-x$

dann

$\displaystyle x^{2}\rightarrow\left( -x\right) ^{2}=x^{2}$

(6.375)

d.h. das Potential des harmonischen Oszillators ist unverändert bei Transformation $x\rightarrow-x$

$\displaystyle V\left( -x\right) =V\left( x\right)$

(6.376)

2. Ableitung

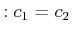$\displaystyle \frac{d^{2}}{dx^{2}}\rightarrow\frac{d^{2}}{\left( d\left( -x\right) \right) ^{2}}=\frac{d^{2}}{dx^{2}}$

(6.377)

sei

$\displaystyle H\left( x\right) \psi\left( x\right) =E\psi\left( x\right)$

(6.378)

wir transformieren $x\rightarrow-x$

$\displaystyle H\left( -x\right) \psi\left( -x\right) =E\psi\left( -x\right)$

(6.379)

nun ist

$\displaystyle H\left( -x\right) =H\left( x\right)$

(6.380)

also

$\displaystyle H\left( x\right) \psi\left( -x\right) =E\psi\left( -x\right)$

(6.381)

d.h. wenn $\psi\left( x\right)$ eine Eigenfunktion von $H\left( x\right)$ ist, ist auch $\psi\left( -x\right)$ eine Eigenfunktion.

Implizite Annahme: zur Energie gibt es nur eine Eigenfunktion (keine Entartung)

also muss

$\displaystyle \psi\left( -x\right) =\alpha\psi\left( x\right)$

(6.382)

$\alpha$ eine komplexe Konstante

wir setzen

$\displaystyle H\left( x\right) \alpha\psi\left( x\right) =E\alpha\psi\left( x\right)$

(6.383)

$\Rightarrow$

$\displaystyle \alpha^{2}H\left( x\right) \psi\left( x\right) =\alpha E\psi\left( x\right)$

(6.384)

Diese Gleichung ist nur erfüllt, wenn $\left\vert a\right\vert =1$

aus $\psi\left( -x\right) =\alpha\psi\left( x\right) =\alpha\left( \alpha\psi\left( -x\right) \right)$

folgt $\alpha^{2}=1$

oder $\alpha=\pm1$

$\displaystyle \Rightarrow\psi\left( x\right) =\left\{ \begin{array}[c]{ccc} +\p... ...\psi\left( x\right) & & \text{asymmetrische Wellenfunktion} \end{array} \right.$

(6.385)

Symmetrien in drei Dimensionen

wir ersetzen

$\displaystyle x\rightarrow\vec{r}$

(6.386)

Transformation

$\displaystyle \vec{r}\rightarrow-\vec{r}$

(6.387)

Ist $H\left( \vec{r}\right)$ invariant gegen $\vec{r}\rightarrow-\vec{r}$ folgt

$\displaystyle \psi\left( -\vec{r}\right)$	$\displaystyle =\pm\psi\left( \vec{r}\right)$ Paritätstransformation	(6.388)
	+ gerade Parität	(6.389)
	- ungerade Parität	(6.390)

$\Rightarrow$ harmonischer Oszillator

.... gerade Parität

,... ungerade Parität

Drehsymmetrie

Sei $H\left( r,\varphi+\varphi_{1}\right) =H\left( r,\varphi\right) \varphi\epsilon R$

und $\vartheta$ sei konstant

Schrödingergleichung

$\displaystyle H\left( r,\varphi+\varphi_{1}\right) \psi\left( r,\varphi+\varphi _{1}\right) =E\psi\left( r,\varphi+\varphi_{1}\right)$

(6.391)

und auch

$\displaystyle H\left( r,\varphi\right) \psi\left( r,\varphi+\varphi_{1}\right) =E\psi\left( r,\varphi+\varphi_{1}\right)$

(6.392)

Da $\psi\left( r,\varphi+\varphi_{1}\right)$ eine Eigenfunktion ist,gilt auch

$\displaystyle \psi\left( r,\varphi+\varphi_{1}\right) =\alpha\left( \varphi_{1}\right) \psi\left( r,\varphi\right)$

(6.393)

für einen zweiten Winkel gilt

$\displaystyle \psi\left( r,\varphi+\varphi_{1}\right) =\alpha\left( \varphi_{2}\right) \psi\left( r,\varphi\right)$

(6.394)

und auch

$\displaystyle \psi\left( r,\varphi+\varphi_{1}+\varphi_{2}\right)$	$\displaystyle =\psi\left( r,\left( \varphi+\varphi_{2}\right) +\varphi_{1}\right) =\alpha\left( \varphi_{1}\right) \psi\left( r,\varphi+\varphi_{2}\right)$	(6.395)
	$\displaystyle =\alpha\left( \varphi_{1}\right) \alpha\left( \varphi_{2}\right) \psi\left( r,\varphi\right)$	(6.396)

andererseits folgt aus

$\displaystyle \psi\left( r,\varphi+\varphi_{s}\right) =\alpha\left( \varphi_{s}\right) \psi\left( r,\varphi\right)$

(6.397)

mit

$\displaystyle \varphi_{s}=\varphi_{1}+\varphi_{2}$

(6.398)

$\displaystyle \psi\left( r,\varphi+\varphi_{1}+\varphi_{2}\right) =\alpha\left( \varphi_{1}+\varphi_{2}\right) \psi\left( r,\varphi\right)$

(6.399)

also muss

$\displaystyle \alpha\left( \varphi_{1}+\varphi_{2}\right) =\alpha\left( \varphi _{1}\right) \alpha\left( \alpha_{2}\right)$

(6.400)

Mathematik sagt, dass die einzig mögliche Lösung

$\displaystyle \alpha\left( \varphi\right) =e^{im\varphi}$

(6.401)

wobei noch unbekannt ist.

Drehung um $2\pi$

$\displaystyle e^{2\pi im}=1$

(6.402)

daraus folgt

$\displaystyle m\in Z$

(6.403)

also

$\displaystyle \psi\left( r,\varphi\right) =e^{im\varphi}\psi\left( r,0\right) m\in Z$

(6.404)

$\Rightarrow$ kompatibel mit magnetischer Quartenzahl im Wasserstoffatom

Auswahlregeln

aus

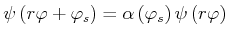$\displaystyle H_{mn}^{s}=\int\limits_{-\infty}^{+\infty}\varphi_{m}^{\ast}\left( x\right) x\varphi_{n}\left( x\right) dx$

(6.405)

schreiben wir

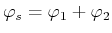$\displaystyle I=\int\limits_{-\infty}^{+\infty}\psi^{\ast}\left( x\right) x\psi\left( x\right) dx$

(6.406)

Transformation $x\rightarrow-x$

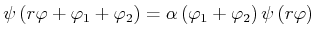$\displaystyle I=\int\limits_{+\infty}^{-\infty}\psi^{\ast}\left( -x\right) \left( -x\right) \psi\left( -x\right) d\left( -x\right)$

(6.407)

Integrationsgrenzen

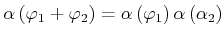$\displaystyle I=\int\limits_{-\infty}^{+\infty}\psi^{\ast}\left( -x\right) \left( -x\right) \psi\left( -x\right) dx$

(6.408)

wenn $x\rightarrow-x$ bleibt $\psi^{\ast}\psi$ als quadratische Fkt gleich

also folgt

$\displaystyle I=-I$

(6.409)

oder

$\displaystyle I=0$

(6.410)

Matrixelemente mit $m\neq n$

falls $\varphi_{n}$ und $\varphi_{m}$ gleiche Parität haben ist ,

bei ungleicher Parität ist $I\neq0$

Dipol-Matrixelemente des Wasserstoffatoms

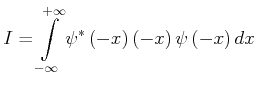$\displaystyle I_{z}=\int\psi_{n,l,m}^{\ast}\left( \vec{r}\right) z\psi_{n^{\prime },l^{\prime},m^{\prime}}\left( \vec{r}\right) dV$

(6.411)

in Polarkoordination

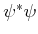$\displaystyle I_{z}=\int\psi_{n,l,m}^{\ast}\left( r,\vartheta,\varphi\right) r\... ...eta\psi_{n^{\prime},l^{\prime},m^{\prime}}\left( r,\vartheta ,\varphi\right) dV$

(6.412)

Wir betrachten Drehungen an die z-Achse um $\varphi_{0}$

wir haben (von früher)

$\displaystyle I_{z}=e^{-i\left( m-m^{\prime}\right) }\varphi_{0_{I_{z}}}$

(6.413)

also ist entweder

$\displaystyle I_{z}=0$

(6.414)

oder

$\displaystyle m^{\prime}=m$

(6.415)

Dipolmomente in x- und y-Richtung

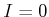$\displaystyle I_{x}$	$\displaystyle =\int\psi_{n,l,m}^{\ast}\left( r,\vartheta,\varphi\right) x\psi_{n^{\prime},l^{\prime},m^{\prime}}\left( r,\vartheta,\varphi\right) dV$	(6.416)
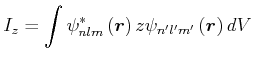$\displaystyle I_{y}$	$\displaystyle =\int\psi_{n,l,m}^{\ast}\left( r,\vartheta,\varphi\right) y\psi_{n^{\prime},l^{\prime},m^{\prime}}\left( r,\vartheta,\varphi\right) dV$	(6.417)
$\displaystyle I_{x}\pm iI_{y}$	$\displaystyle =\int\psi_{n,l,m}^{\ast}\left( r,\vartheta,\varphi \right) \left[... ...t] \psi_{n^{\prime},l^{\prime},m^{\prime} }\left( r,\vartheta,\varphi\right) dV$	(6.418)

mit

$\displaystyle x\pm iy=r\cos\varphi\sin\vartheta\pm irsm\varphi\sin\vartheta=re^{\pm i\varphi}\sin\vartheta$

(6.419)

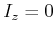$\displaystyle I_{x}\pm iI_{y}=\int\psi_{n,l,m}^{\ast}\left( r,\vartheta,\varphi... ...phi}\psi_{n^{\prime},l^{\prime},m^{\prime}}\left( r,\vartheta,\varphi\right) dV$

(6.420)

Wir drehen um $\varphi_{0}$ um die z-Achse

also wird

$\displaystyle \psi_{n,l,m}^{\ast}\left( r,\vartheta,\varphi+\varphi_{0}\right)$	$\displaystyle =e^{-im\varphi_{0}}\psi_{n,l,m}^{\ast}\left( r,\vartheta,\varphi\right)$	(6.421)
$\displaystyle \psi_{n^{\prime},l^{\prime},m^{\prime}}\left( r,\vartheta,\varphi+\varphi _{0}\right)$	$\displaystyle =e^{im^{\prime}\varphi_{0}}\psi_{n^{\prime},l^{\prime },m^{\prime}}\left( r,\vartheta,\varphi\right)$	(6.422)
$\displaystyle e^{\pm i\left( \varphi+\varphi_{0}\right) }$	$\displaystyle =e^{\pm i\varphi}e^{\pm i\varphi_{0}}$	(6.423)

also haben wir

$\displaystyle I_{x}\pm iI_{y}$	$\displaystyle =e^{im^{\prime}\varphi_{0}}e^{\pm i\varphi_{0} }e^{-im\varphi_{0}}\left( I_{x}+iI_{y}\right)$	(6.424)
	$\displaystyle =e^{i\left( m^{\prime}\pm1-m\right) \varphi_{0}}\left( I_{x} +iI_{y}\right)$	(6.425)

also entweder

$\displaystyle I_{x}+iI_{y}$	$\displaystyle = 0$ für $\displaystyle m\neq m^{\prime}+1$	(6.426)
$\displaystyle I_{x}-iI_{y}$	$\displaystyle = 0$ für $\displaystyle m\neq m^{\prime}-1$	(6.427)

in jedem Falle ist dann

$\displaystyle I_{x}$	$\displaystyle = 0$	(6.428)
$\displaystyle I_{y}$	$\displaystyle = 0$	(6.429)

Auswahlregeln:

$m=m^{\prime}$ $I_{z}\neq0$ linear polarisiertes Licht ( $\pi$ -Polarisation)

$m=m^{\prime}\pm1$ $\begin{displaymath} \begin{array}[c]{c} I_{x}+iI_{y}\neq0\\ I_{x}-iIy\neq0 \end{array}\end{displaymath}$ zirkular polarisiert ( $\pm$ $\sigma$ -Polarisation)

Ohne Ableitung

$\displaystyle l=l^{\prime}\pm1$

(6.430)

Next: Mehrelektronenatome Up: Atome und ihr Aufbau Previous: Atome im elektrischen Feld Skript: PDF-Datei Übungen: Blätter

Othmar Marti
Experimentelle Physik
Universiät Ulm

$m=m^{\prime}$	$I_{z}\neq0$	linear polarisiertes Licht	( $\pi$ -Polarisation)
$m=m^{\prime}\pm1$	$\begin{displaymath} \begin{array}[c]{c} I_{x}+iI_{y}\neq0\\ I_{x}-iIy\neq0 \end{array}\end{displaymath}$	zirkular polarisiert	( $\pm$ $\sigma$ -Polarisation)