
Weiter: Mechanik in einer Dimension Oben: Einführung Zurück: Einführung Skript: PDF-Datei Übungen: Blätter ILIAS: Materialien Korrekturen
Eine physikalische Grösse besteht aus der Masszahl und der Einheit
Beispiel:
![\includegraphics[width=0.3\textwidth]{einfuehrung-005}](img29.gif)
| Gleichungen müssen nicht nur für die Masszahlen sondern auch für Einheiten gelten, das heisst, dass man mit einer Einheitenbetrachtung feststellen kann, dass eine Gleichung falsch ist. |
Beispiel:
|
Die SI-Einheiten sind die gesetzlichen Einheiten. Das SI ist überbestimmt, nur die Einheiten der Länge, der Zeit und der Masse wären notwendig.
| (2.1) |
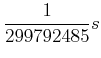 |
(2.2) |
d.h. Lichtgeschwindigkeit ![]() ist definiert, nicht die Länge. Man könnte
ist definiert, nicht die Länge. Man könnte ![]() setzen und die Länge in Sekunden
messen.
setzen und die Länge in Sekunden
messen.
Grössen werden im cgs-System durch
![]() ,
,![]() ,
,![]() ausgedrückt
ausgedrückt
|
|
Eine Grösse messen heisst, das zu messende Objekt mit der Masseinheit zu vergleichen.
Es gibt auch indirekte Messmethoden, z.B. bei Thermometern
|
|
Bei jeder Messung gibt es eine Messunsicherheit
|
Messunsicherheiten werden wie folgt kategorisiert
Wir betrachten die Fehlerfortpflanzung anhand der Geschwindigkeitsmessung. Die Geschwindigkeit kann aus
der Zeit ![]() , die zum Durchlaufen einer bestimmten Strecke
, die zum Durchlaufen einer bestimmten Strecke ![]() benötigt wird, berechnet werden. Wir nehmen an,
dass wir
benötigt wird, berechnet werden. Wir nehmen an,
dass wir ![]() Messungen durchführen, und dabei die Messungen mit
Messungen durchführen, und dabei die Messungen mit
![]() bezeichnen. Wir verwenden fernen den
Mittelwert der Ortsmessung
bezeichnen. Wir verwenden fernen den
Mittelwert der Ortsmessung
und den Mittelwert der Zeitmessung
Die Abweichung der einzelnen Messwerte vom Mittelwert ist dann
Die Standardabweichung eines einzelnen Messwertes einer Grösse ![]() bei
bei ![]() Messungen ist definiert durch
Messungen ist definiert durch
Die Standardabweichung des Mittelwertes
![]() einer Grösse
einer Grösse ![]() bei
bei ![]() Messungen ist
Messungen ist
Die einzelnen Messwerte können dann auch als
Es gelten
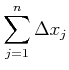 |
||
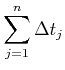 |
Mit
![]() wird
wird
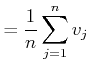 |
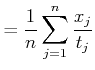 |
||
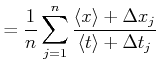 |
|||
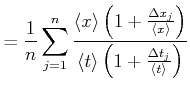 |
|||
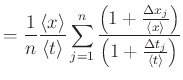 |
|||
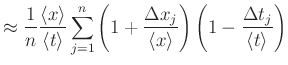 |
|||
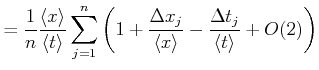 |
|||
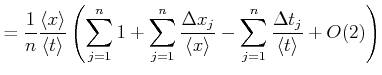 |
|||
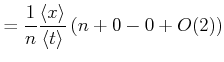 |
|||
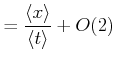 |
Dies bedeutet, dass man für statistisch unabhängige Daten sowohl zuerst das Resultat ausrechnen kann und dann
mitteln, oder zuerst die Messwerte Mitteln, und dann das Resultat berechnen kann. Die beiden Resultate werden bis
auf Summanden der Ordnung ![]() in den Fehlern identisch sein.
in den Fehlern identisch sein.
Der Begriff ![]() sagt, dass Terme mit der Ordnung (Summe aller Exponenten) von 2 oder mehr vernachlässigt
wurden.
sagt, dass Terme mit der Ordnung (Summe aller Exponenten) von 2 oder mehr vernachlässigt
wurden.
Die Messunsicherheit von
![]() wird durch
wird durch
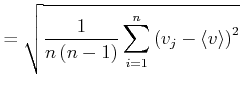 |
Ein einzelner berechneter Wert der Geschwindigkeit wird dann
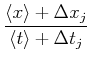 |
||
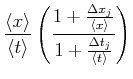 |
||
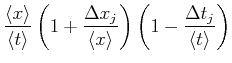 |
||
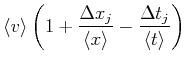 |
||
Zufällige Fehler sind Gauss-verteilt. Der relative Fehler des Mittelwertes aller Messungen nimmt meist mit
![]() (wobei
(wobei ![]() die Anzahl Messungen ist) ab. Die Messunsicherheit von
die Anzahl Messungen ist) ab. Die Messunsicherheit von
![]() wird durch
wird durch
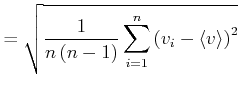 |
||
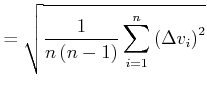 |
||
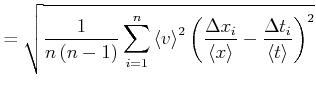 |
||
![$\displaystyle = \left<v\right>\sqrt{\frac{1}{n\left(n-1\right)}\sum\limits_{i=1...
...2\frac{\Delta x_{i}}{\left<x\right>}\frac{\Delta t_{i}}{\left<t\right>}\right]}$](img105.gif) |
Nun ist aber
![]() und
und
![]() nach unseren Annahmen statistisch unabhängig, also nicht korreliert.
Daraus folgt, dass das Produkt
nach unseren Annahmen statistisch unabhängig, also nicht korreliert.
Daraus folgt, dass das Produkt
![]() sich zu null mittelt
und weggelassen werden kann. Wir haben also
sich zu null mittelt
und weggelassen werden kann. Wir haben also
![$\displaystyle = \sqrt{\frac{1}{n\left(n-1\right)}\sum\limits_{i=1}^n \left[\lef...
...t<x\right>}\right)^2+\left(\frac{\Delta t_{i}}{\left<t\right>}\right)^2\right]}$](img110.gif) |
||
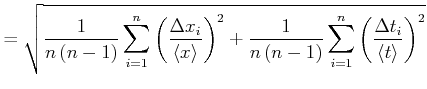 |
||
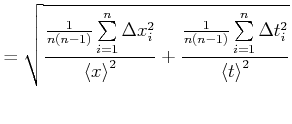 |
||
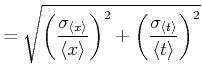 |
Im besprochenen Falle haben wir eine Funktion, die als Polynom geschrieben werden kann. Deshalb lässt sich das
Fehlerfortpflanzungsgesetz relativ schreiben. Im Allgemeinen gilt: wenn
![]() ist, lautet das Gausssche Fehlerfortpflanzungsgesetz
ist, lautet das Gausssche Fehlerfortpflanzungsgesetz
Andererseits könnte man auch so argumentieren: Wir ersetzen die Messwerte durch die Schätzwerte ![]() und
und
![]() . Wir erhalten (ohne Berücksichtigung der Vorzeichen, da wir dies ja nicht kennen)
. Wir erhalten (ohne Berücksichtigung der Vorzeichen, da wir dies ja nicht kennen)
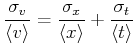
Allgemein gilt: wenn
![]() ist, ist
ist, ist
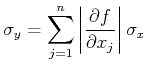
Diese letzteren Rechnungen (Grösstfehlerabschätzung) sollten nicht verwendet werden. Sie liefern bis zu zehn mal zu hohe Fehlerschranken.
Othmar Marti