Weiter: Schwingungen und eindimensionale Wellen Oben: Mechanik deformierbarer Medien Zurück: Oberflächenspannung Skript: PDF-Datei Übungen: Blätter ILIAS: Materialien Korrekturen
![\includegraphics[width=0.5\textwidth]{deform-024}](img2927.gif)
|
An jedem Punkt hat die Geschwindigkeit
![]() einen Betrag und eine Richtung.
einen Betrag und eine Richtung.
Das Vektorfeld
![]() ist durch Stromlinien charakterisiert. Wenn
ist durch Stromlinien charakterisiert. Wenn
![]() nicht von der Zeit abhängt, heisst die Strömung stationär.
nicht von der Zeit abhängt, heisst die Strömung stationär.
Bahnlinien: Bahn eines Teilchens
Bei stationären Strömungen sind Bahnlinien und Stromlinien identisch. Inkompressible Strömungen sind Strömungen
mit konstanter Dichte ![]() .
.
![\includegraphics[width=0.3\textwidth]{deform-025}](img2929.gif)
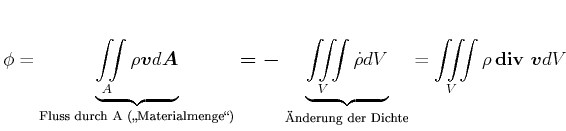
Fluss
|
Der Fluss ist definiert als
| (7.722) |
oder
| (7.723) |
Integralform
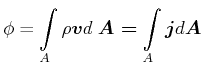 |
(7.724) |
wobei ![]() beliebige Fläche (auch gekrümmt) und
beliebige Fläche (auch gekrümmt) und
![]() die Stromdichte ist (analog zum elektrischen
Strom). Bei einer geschlossenen Fläche fliesst netto ein Medium heraus, wenn eine Quelle im Volumen ist.
die Stromdichte ist (analog zum elektrischen
Strom). Bei einer geschlossenen Fläche fliesst netto ein Medium heraus, wenn eine Quelle im Volumen ist.
![\includegraphics[width=0.7\textwidth]{deform-026}](img2934.gif)
Berechnung der Divergenz
|
Wir haben
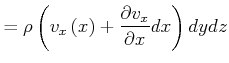 |
Netto:
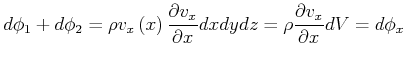
ebenso:
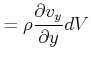 |
||
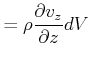 |
(7.725) |
Der Nettofluss ergibt sich zu
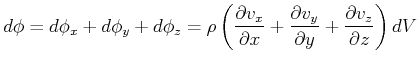 |
(7.726) |
Ohne Quelle ist ![]() , d.h. die Grösse
, d.h. die Grösse
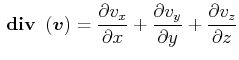 |
(7.727) |
Die Divergenz beschreibt die Quellen und Senken in einem Fluss.
Wenn
![]() ist, so muss sich die Dichte an dieser Stelle ändern
ist, so muss sich die Dichte an dieser Stelle ändern
| (7.728) |
oder
| (7.729) |
Dies ist die Kontinuitätsgleichung.
![]() heisst Quelldichte.
heisst Quelldichte.
Eine quellenfreie inkompressible Strömung hat überall
![]() .
.
Es gilt:
 |
(7.730) |
Der Satz von Gauss besagt
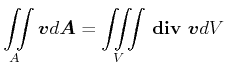 |
(7.731) |
![\includegraphics[width=0.7\textwidth]{deform-028}](img2955.gif)
Geschwindigkeitsgradient und Rotation
|
Wenn die Strömung inhomogen ist, werden mitgeführte Teilchen gedreht.
Wasser strömt mit
![]() am Würfel vorbei. Wir haben ein Gleichgewicht, wenn
am Würfel vorbei. Wir haben ein Gleichgewicht, wenn
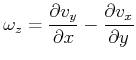 |
(7.732) |
![]() zeigt in die
zeigt in die ![]() Richtung. Im Allgemeinen ist
Richtung. Im Allgemeinen ist
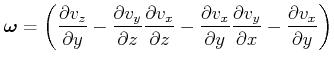 |
(7.733) |
mit
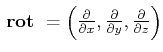 wird
wird
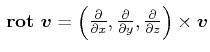 die Rotation des Strömungsfeldes.
die Rotation des Strömungsfeldes.
Es gilt dann
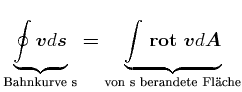 |
(7.734) |
Falls
![]() ist kann
ist kann ![]() aus dem Geschwindigkeitspotential
aus dem Geschwindigkeitspotential ![]() abgeleitet werden.
abgeleitet werden.
| (7.735) |
Dann gilt
![]()
Für inkompressible Flüssigkeiten gilt
| (7.736) |
Wir haben also drei unterschiedliche physikalische Phänomene, die durch die gleiche Mathematik beschrieben werden:
Strömung
![]() Graviation
Graviation
![]() Elektrostatik
Elektrostatik
![\includegraphics[width=0.7\textwidth]{deform-029}](img2966.gif)
Mitbewegtes System
|
Sei ![]() das Laborsystem,
das Laborsystem, ![]() das mitbewegte System,das
das mitbewegte System,das ![]() folgt. Seien
folgt. Seien ![]() lokale zeitliche
Ableitungen und
lokale zeitliche
Ableitungen und ![]() totale zeitliche Ableitungen
totale zeitliche Ableitungen
Das 2. Newtonsches Gesetz beschreibt die Bewegung von ![]() aber nur in
aber nur in
![]()
(in ![]() betrachtet man Volumina, nicht Massen)
betrachtet man Volumina, nicht Massen)
Also ist
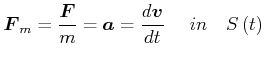 |
(7.737) |
Lokale Ableitung:
![]() ist in
ist in ![]() fest
fest
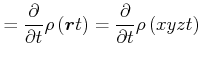 |
||
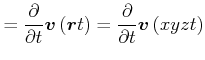 |
(7.738) |
Totale zeitliche Ableitungen
In
![]() beschreiben die physikalischen Grössen das gleiche Teilchen.
beschreiben die physikalischen Grössen das gleiche Teilchen.
| (7.739) |
wobei
![]() die Koordinaten in
die Koordinaten in ![]() sind
sind
| (7.740) |
Ableitung: totale Ableitung auf der Bahn
![]()
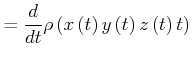 |
||
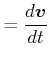 |
(7.741) |
Zusammenhang:
Dichte
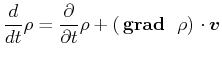 |
(7.742) |
Beweis:
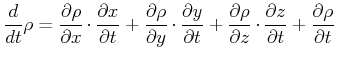 |
(7.743) |
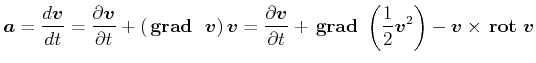 |
(7.744) |
Grund Massenerhaltung
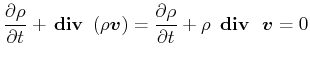 |
(7.745) |
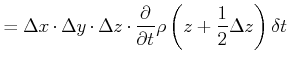 |
||
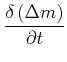 |
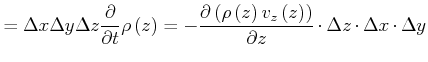 |
|
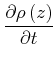 |
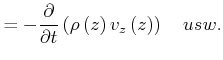 |
(7.746) |
![\includegraphics[width=0.5\textwidth]{deform-027}](img2997.gif)
|
Die Stromlinien durch ![]() definieren einen Schlauch, die Stromröhre, die keinen Austausch mit der Umgebung hat.
Also ist in einer inkompressiblen Flüssigkeit
definieren einen Schlauch, die Stromröhre, die keinen Austausch mit der Umgebung hat.
Also ist in einer inkompressiblen Flüssigkeit
| (7.747) |
Dies ist die makroskopische Kontinuitätsgleichung.
Sei
![]() . Dann ist die Dichte
. Dann ist die Dichte
![]() und die Kontinuitätsgleichung
und die Kontinuitätsgleichung
![]() .
.
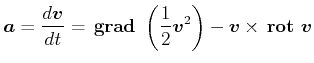 |
(7.748) |
Im Stromfaden gilt
| (7.749) |
Inkompressible Flüssigkeiten
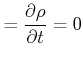 |
||
| (7.750) |
dann gilt
![]()
![\includegraphics[width=0.4\textwidth]{deform-030}](img3007.gif)
|
Moleküle haben am Rand im Mittel die Geschwindigkeit der Wand.
![]() ist parallel zur Wand.
ist parallel zur Wand.
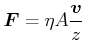 |
(7.751) |
![]() heisst Viskosität (Scherviskosität)
heisst Viskosität (Scherviskosität)
Beispiel
Wasser:
![]()
Glyzerin
![]()
Allgemein:
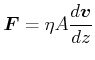 |
(7.752) |
wobei ![]() klein sein soll.
klein sein soll.
Temperaturabhängigkeit:
Moleküle müssen ihren Platz wechseln (
![]() Bolzmannstatistik)
Bolzmannstatistik)
| (7.753) |
![\includegraphics[width=0.3\textwidth]{deform-031}](img3015.gif)
Viskose Strömung um einen Quader
|
Laminare Stromlinien sind dadurch charakterisiert, dass benachbarte Stromlinien benachbart bleiben (Beispiel: Blut)
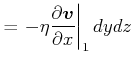 |
||
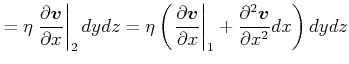 |
||
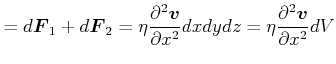 |
(7.754) |
Allgemein:
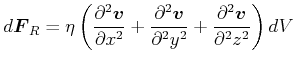 |
(7.755) |
oder
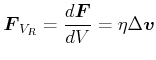 |
(7.756) |
Die Druckkraft ist
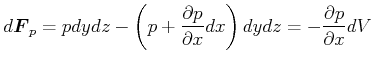 |
(7.757) |
also
| (7.758) |
![]() und
und
![]() beschreiben die Dynamik
beschreiben die Dynamik
![\includegraphics[width=0.3\textwidth]{deform-032}](img3028.gif)
|
![]() an der Wand
an der Wand
![]() in der Mitte
in der Mitte
![]() Reibungskraft
Reibungskraft
![]()
Druck:
![]()
![]()
![]() ist eine Parabel
ist eine Parabel
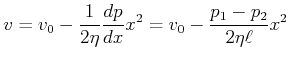
Am Rand ist ![]()
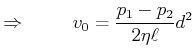
![\includegraphics[width=0.2 \textwidth]{deform-033}](img3038.gif)
Rohrströmung
|
Am Rand ist die Geschwindigkeit null, ![]() .
.
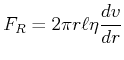
also
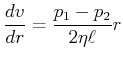
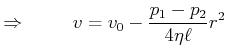
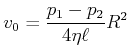
infinitesimal
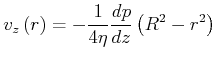
Volumenstrom:
![]()
also:
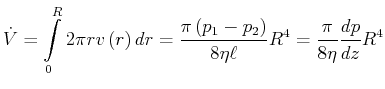 |
(7.759) |
Das ist das Gesetz von Hagen-Poiseuille, wobei
![]() und
und
![]()
Der Strömungswiderstand ist:
![]()
Druckkraft
![]()
![\includegraphics[width=0.4\textwidth]{deform-034}](img3051.gif)
|
Die Kugel hat im Abstand ![]() keinen Einfluss mehr auf die Strömung
keinen Einfluss mehr auf die Strömung
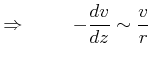
Oberfläche:
![]()
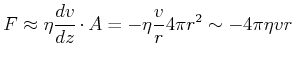
Genauer erhält man
| (7.760) |
![\includegraphics[width=0.7\textwidth]{deform-035}](img3056.gif)
|
Reibungskraft:
![]()
Verschieben um ![]() :
:
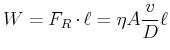 |
(7.761) |
Kinetische Energie in der Grenzschicht:
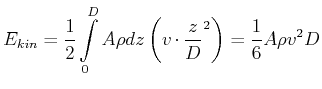 |
(7.762) |
mit ![]() wird
wird
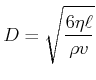
Reynolds-Kriterium
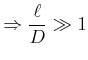 |
||
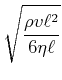 |
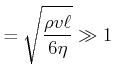 |
(7.763) |
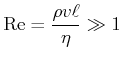 |
(7.764) |
dabei ist ![]() eine typische Dimension und
eine typische Dimension und ![]() die mittlere Geschwindigkeit.
die mittlere Geschwindigkeit.
wenn
Allgemein gilt: Es gibt für jede Geometrie eine kinetische Reynoldszahl. ![]() mit
mit
| (7.765) |
Bemerkung:
Strömungen mit der gleichen Reynoldszahl sind ähnlich
![]() Windkanal
Windkanal
Bei ![]() ist
ist
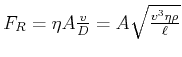
![]() ist etwa der Mittelwert aus
ist etwa der Mittelwert aus
Neben der Scherviskosität existiert noch die Volumenviskosität ![]()
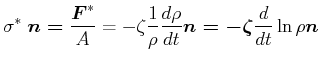 |
(7.766) |
Dabei ist ![]() die Volumenviskosität.
die Volumenviskosität.
Das Gesetz von Navier-Stokes lautet
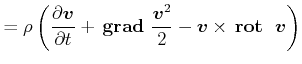 |
||
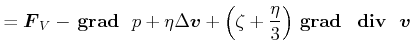 |
||
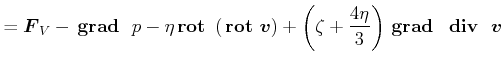 |
(7.767) |
Vereinfachungen:
![\includegraphics[width=0.7\textwidth]{deform-036}](img3089.gif)
|
Bei einer idealen Strömung gibt es keine Reibung, die Strömung ist laminar.
Aus der Volumenerhaltung folgt
Wir erhalten als Energiebilanz
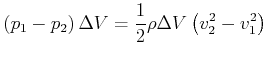 |
Das ergibt nun
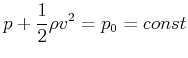 |
(7.768) |
Dies ist die Bernoulli-Gleichung.
Bei der Gravitation muss noch ![]() berücksichtigt werden (allg.
berücksichtigt werden (allg. ![]()
![\includegraphics[width=0.5\textwidth]{deform-037}](img3098.gif)
Manometer
|
Ein Manometer misst nur den statischen Druck.
![\includegraphics[width=0.4\textwidth]{deform-038}](img3099.gif)
Prandtlsches Staurohr
|
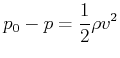 |
(7.769) |
![\includegraphics[width=0.4\textwidth]{deform-039}](img3101.gif)
Ausströmen aus einem Loch
|
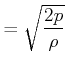 |
(7.770) |
Bei Schweredruck ![]() folgt
folgt
![]()
Wenn
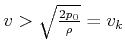 wird der statische Druck
wird der statische Druck ![]()
Es gibt eine Dampfbildung (Kavitation).
![\includegraphics[width=0.5\textwidth]{deform-040}](img3108.gif)
Stromlinie
|
Nach Bernoulli ist der Druck vorne und hinten gleich. Also gäbe es keinen Widerstand (Paradoxon von d'Alembert).
![\includegraphics[width=0.7\textwidth]{deform-041}](img3109.gif)
Reales Bild einer Wirbelstrasse
|
Def. Wirbel: Wenn ein Boot auf einem geschlossenen Weg angetrieben wird
Def. Zirkulation :
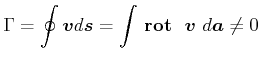 |
(7.771) |
![\includegraphics[width=0.3\textwidth]{deform-042}](img3111.gif)
Potentialwirbel
|
| (7.772) | ||
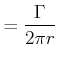 |
(7.773) |
Beim Potentialwirbel gilt:
![\begin{displaymath}
\left.
\begin{array}[c]{c}
{}\boldsymbol{\mathrm{rot}}{} \...
...ein Geschwindigkeitspotential }\phi=\frac{\Gamma}{2\pi}\varphi
\end{displaymath}](img3113.gif)
Nach Bernoulli:
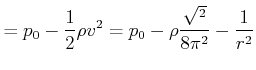 |
||
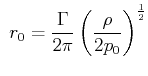 |
(7.774) |
d.h. für ![]() ist das Konzept des Potentialwirbels nicht sinnvoll.
ist das Konzept des Potentialwirbels nicht sinnvoll.
Volumenkraft
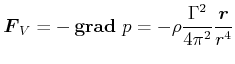 |
(7.775) |
(nach innen gerichtet)
![\includegraphics[width=0.7\textwidth]{deform-043}](img3118.gif)
Helmholtzsche Wirbelsätze
|
Othmar Marti