Weiter: Wellen in einer Dimension Oben: Schwingungen und eindimensionale Wellen Zurück: Schwingungen und eindimensionale Wellen Skript: PDF-Datei Übungen: Blätter ILIAS: Materialien Korrekturen
(Siehe Tipler, Physik [Tip94, pp. 379]) (Siehe Gerthsen, Physik [Mes04, pp. 141])
Wenn sich ein System nicht in seiner Gleichgewichtslage befindet, dann schwingt in der Regel seine Position um diese Lage. Diese periodischen oder quasiperiodischen Bewegungen werden Schwingungen genannt. Die Schwingungsform kann sinusförmig sein (harmonische Schwingung) oder eine allgemeine Form haben. Mathematische Sätze sagen, dass jede periodische Bewegung in eine Summe von sinusförmigen Bewegungen aufgeteilt werden kann.
|
|
(Siehe Tipler, Physik [Tip94, pp. 379]) (Siehe Gerthsen, Physik [Mes04, pp. 141])
![\includegraphics[width=0.6\textwidth]{schwingung-masse-feder}](img3119.gif)
Masse-Feder-System als Modell eines schwingungsfähigen Systems
|
Die Kraft auf die Masse ist durch
| (8.776) |
gegeben, wobei ![]() die Federkonstante ist. Durch diese Kraft wird die Masse beschleunigt, so
dass
die Federkonstante ist. Durch diese Kraft wird die Masse beschleunigt, so
dass
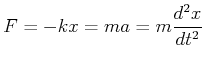
Umgeschrieben erhalten wir die Bewegungsgleichung
Die Beschleunigung ist also proportional zur Auslenkung. Traditionellerweise wird die obige Gleichung auch als
|
Frequenzen werden in Hertz |
Die Lösung der Gleichung (8.3) ist
| (8.779) |
|
|
|
|
Diese Lösung wird durch die
Simulation
illustriert. Die
Phase ist nur bis auf ein ganzzahliges Vielfaches von ![]() bestimmt (Eigenschaft der Winkelfunktionen). Die
Position beim Nulldurchgänge ist
bestimmt (Eigenschaft der Winkelfunktionen). Die
Position beim Nulldurchgänge ist
![]() .
.
| Ist die Beschleunigung eines Gegenstandes proportional zu seiner Auslenkung und dieser entgegengesetzt, so führt der Gegenstand eine einfache harmonische Schwingung durch. |
Die Geschwindigkeit der Masse ist
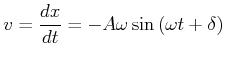 |
(8.780) |
Die Geschwindigkeit bei ![]() ist
ist
![]() . Da von den drei die Schwingung
bestimmenden Grössen zwei,
. Da von den drei die Schwingung
bestimmenden Grössen zwei, ![]() und
und ![]() unbekannt sind, reicht die Kenntnis der Position zur Zeit
unbekannt sind, reicht die Kenntnis der Position zur Zeit ![]() und
der Geschwindigkeit zu dieser gleichen Zeit aus, um die Schwingungsform zu bestimmen.
und
der Geschwindigkeit zu dieser gleichen Zeit aus, um die Schwingungsform zu bestimmen.
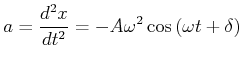 |
(8.781) |
Mit Gleichung (8.2) kann man schreiben
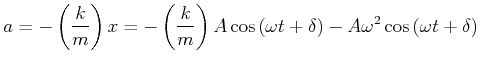 |
(8.782) |
und damit
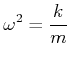 |
(8.783) |
Damit sind die Frequenz ![]() und die Schwingungsdauer
und die Schwingungsdauer ![]()
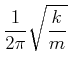 |
|||
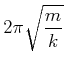 |
(8.784) |
(Siehe Tipler, Physik [Tip94, pp. 387])
![\includegraphics[width=0.4\textwidth]{schwingungen-kreisbewegung}](img3139.gif)
Zusammenhang zwischen der Kreisbewegung und einer Schwingung
|
Da die Funktionen
![]() und
und
![]() beide die Schwingungsgleichung
erfüllen, kann geschlossen werden, dass eine harmonische Schwingung die Projektion einer Kreisbewegung ist (siehe
auch die Simulation). Nach der Definition des
Cosinus ist die Projektion des umlaufenden Radius
beide die Schwingungsgleichung
erfüllen, kann geschlossen werden, dass eine harmonische Schwingung die Projektion einer Kreisbewegung ist (siehe
auch die Simulation). Nach der Definition des
Cosinus ist die Projektion des umlaufenden Radius ![]() auf die
auf die ![]() -Achse gerade der Cosinus.
-Achse gerade der Cosinus.
|
|
(Siehe Tipler, Physik [Tip94, pp. 388])
Die potentielle Energie einer um die Länge ![]() ausgelenkten Feder ist
ausgelenkten Feder ist
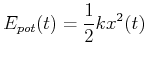 |
(8.785) |
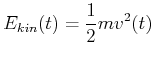 |
(8.786) |
Beide Energien hängen von der Zeit ab. Die Erhaltung der mechanischen Energie fordert
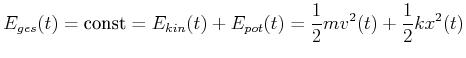 |
(8.787) |
Am Umkehrpunkt, bei der maximalen Auslenkung
![]() ist die Geschwindigkeit
ist die Geschwindigkeit ![]() . Also ist bei
einem harmonischen Oszillator
. Also ist bei
einem harmonischen Oszillator
Setzen wir die Lösung
![]() und damit auch
und damit auch
![]() jeweils ein, erhalten wir
jeweils ein, erhalten wir
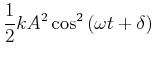 |
|||
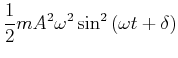 |
|||
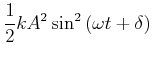 |
(8.789) |
wobei wir
![]() verwendet haben. Die Gesamtenergie ist
verwendet haben. Die Gesamtenergie ist
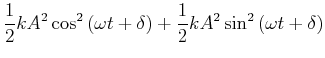 |
|||
![$\displaystyle \frac{1}{2} k A^2 \left[\sin^2\left( \omega t +
\delta\right)+\cos^2 \left(\omega t + \delta\right)\right]$](img3158.gif) |
|||
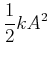 |
(8.790) |
unabhängig von ![]() . Der Energieinhalt eines harmonischen Oszillators pendelt zwischen zwei
Energiereservoirs, hier der kinetischen und der potentiellen Energie, hin und her.
. Der Energieinhalt eines harmonischen Oszillators pendelt zwischen zwei
Energiereservoirs, hier der kinetischen und der potentiellen Energie, hin und her.
| Immer dann, wenn in einem System zwei Energiereservoirs gekoppelt sind und Energie zwischen ihnen ausgetauscht wird, ist das System ein Oszillator. |
Beispiele:
Die kinetische und die potentielle Energie können mit dem Winkel der momentanen Phase
![]() wie folgt geschrieben werden:
wie folgt geschrieben werden:
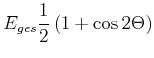 |
|||
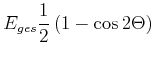 |
(8.791) |
Damit ist auch sofort klar, dass die Mittelwerte
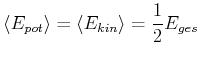 |
(8.792) |
sind.
Bei einer Schwingung|harmonisch ist
Im Phasenbild wird nun ![]() gegen
gegen ![]() aufgetragen. Dabei ist die
Zeit
aufgetragen. Dabei ist die
Zeit ![]() der Parameter. Wir sprechen auch von einer
Parameterdarstellung.
der Parameter. Wir sprechen auch von einer
Parameterdarstellung.
![\includegraphics[width=0.6\textwidth]{phasenbild}](img3169.gif)
Phasenbild eines harmonischen Oszillators
|
Das Phasenbild zeigt den Zusammenhang zwischen Ort und Geschwindigkeit, nicht jedoch den Zeitlichen Ablauf. Phasenbilder werden zum Beispiel verwendet, um chaotische System zu beschreiben.
Zeichnet man
![]() gegen
gegen ![]() auf, so nennt man die Fläche
auf, so nennt man die Fläche
| (8.793) |
Die Einheit dieses ![]() ist
ist
![]() .
Dies ist die gleiche Einheit wie beim Planckschen Wirkungsquantum. Die von
einem Zustand im Phasenbild eingenommene Fläche sagt also etwas aus, wie nahe
dieser Zustand einem Quantenzustand ist.
.
Dies ist die gleiche Einheit wie beim Planckschen Wirkungsquantum. Die von
einem Zustand im Phasenbild eingenommene Fläche sagt also etwas aus, wie nahe
dieser Zustand einem Quantenzustand ist.
(Siehe Tipler, Physik [Tip94, pp. 392])
![\includegraphics[width=0.4\textwidth]{schwingungen-schwerefeld}](img3173.gif)
Schwingendes System im Schwerefeld
|
Eine Feder im Schwerefeld mit Masse wird durch die Bewegungsgleichung
beschrieben (1. Simulation
und
2. Simulation). Die Ruhelage ist durch
![]() gegeben. Also ist
gegeben. Also ist
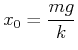 |
(8.795) |
|
|
|
|
Wir wissen, wie wir ein Feder-Masse-System berechnen müssen, wenn wir die Koordinate
![]() verwenden. Da
die beiden Koordinatensysteme
verwenden. Da
die beiden Koordinatensysteme ![]() und
und ![]() sich nur um eine Konstante unterscheiden, sind die ersten Ableitungen
sich nur um eine Konstante unterscheiden, sind die ersten Ableitungen
![]() und die zweiten Ableitungen
und die zweiten Ableitungen
![]() gleich.
Deshalb wird Gleichung (8.19)
gleich.
Deshalb wird Gleichung (8.19)
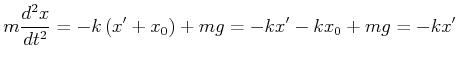 |
(8.796) |
da ![]() ist. Damit erhalten wir die bekannte Lösung
ist. Damit erhalten wir die bekannte Lösung
| (8.797) |
Die potentielle Energie bezogen auf die neue
Gleichgewichtslage ![]() ist
ist
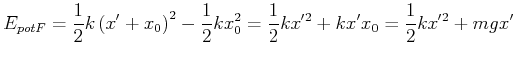 |
(8.798) |
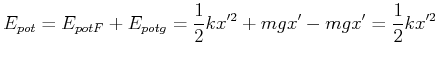 |
(8.799) |
(Siehe Tipler, Physik [Tip94, pp. 394])
![\includegraphics[width=0.55\textwidth]{schwingung-pendel}](img3187.gif)
|
Ein mathematisches Pendel ist eine Punktmasse ![]() aufgehängt an einem masselosen Faden der
Länge
aufgehängt an einem masselosen Faden der
Länge ![]() .
.
Der vom Pendel zurückgelegte Weg ist die Bogenlänge
| (8.800) |
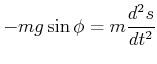 |
(8.801) |
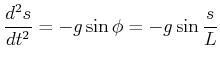 |
(8.802) |
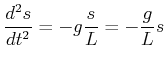 |
(8.803) |
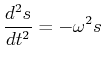 |
(8.804) |
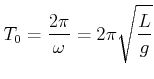 |
(8.805) |
|
|
Für grosse Amplituden ist die Schwingungsdauer durch die Reihenentwicklung
![$\displaystyle T_0 = 2\pi\sqrt{\frac{L}{g}}\left[1+\frac{1}{2^2}\sin^2\left(\fra...
...t(\frac{3}{4}\right)^2\sin^4\left(\frac{1}{2}\frac{s_0}{L}\right)+\ldots\right]$](img3200.gif) |
(8.806) |
![\includegraphics[width=0.34\textwidth]{schwingung-phys-pendel}](img3201.gif)
|
Wir müssen nun mit dem Trägheitsmoment des Pendels bezüglich des Drehpunktes ![]() rechnen. Das
Drehmoment ist
rechnen. Das
Drehmoment ist
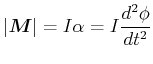 |
(8.807) |
Die Bewegungsgleichung ist also
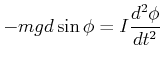 |
(8.808) |
In der traditionellen Schreibweise lautet die Bewegungsgleichung
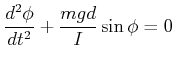 |
(8.809) |
Mit
![]() und unter der Annahme einer kleinen Amplitude ist das physikalische
Pendel ein harmonischer Oszillator mit der Bewegungsgleichung
und unter der Annahme einer kleinen Amplitude ist das physikalische
Pendel ein harmonischer Oszillator mit der Bewegungsgleichung
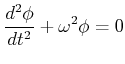 |
(8.810) |
Die Schwingungsdauer ist
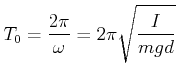 |
(8.811) |
Eine Anwendungsmöglichkeit dieser Gleichung ist die Bestimmung des Trägheitsmomentes eines Körpers
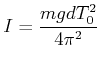 |
(8.812) |
Zum Beispiel ist für einen einseitig eingespannten Stab das Trägheitsmoment
![]() .
Der Schwerpunkt liegt in der Mitte, also
.
Der Schwerpunkt liegt in der Mitte, also
![]() . Damit wird die Schwingungsdauer
. Damit wird die Schwingungsdauer
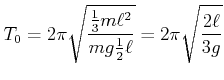
Vergleiche dies mit dem Resultat für ein mathematisches Pendel
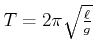 .
.
![\includegraphics[width=0.45\textwidth]{schwingung-torsions-pendel}](img3213.gif)
Torsionspendel (analog zur Gravitationswaage)
|
|
|
Das rückstellende Moment ist proportional zum Verdrillungswinkel und dient zur Winkelbeschleunigung des
Drehkörpers mit dem Trägheitsmoment ![]()
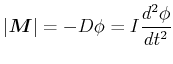 |
(8.813) |
Wieder setzen wir
![]() . Die Periodendauer ist
. Die Periodendauer ist
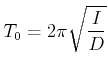 |
(8.814) |
(Siehe Tipler, Physik [Tip94, pp. 400])
Wir nehmen eine allgemeine Potentialfunktion
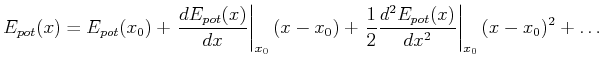 |
(8.815) |
an und entwickeln sie in eine Taylorreihe um den Punkt ![]() . Dieser Punkt soll ein Gleichgewichtspunkt
sein. Dann ist die Kraft
. Dieser Punkt soll ein Gleichgewichtspunkt
sein. Dann ist die Kraft
![]() als Funktion durch die erste Ableitung der
potentiellen Energie gegeben. Am Gleichgewichtspunkt ist jedoch die Kraft null, also
als Funktion durch die erste Ableitung der
potentiellen Energie gegeben. Am Gleichgewichtspunkt ist jedoch die Kraft null, also
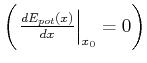 . Die Steigung der Kraft-Distanz-Kurve im
Gleichgewichtspunkt
. Die Steigung der Kraft-Distanz-Kurve im
Gleichgewichtspunkt ![]() , die Federkonstante
, die Federkonstante ![]() , ist durch die zweite Ableitung gegeben.
, ist durch die zweite Ableitung gegeben.
Also kann an jedem Gleichgewichtspunkt bei genügend kleinen Auslenkungen die Schwingungsgleichung
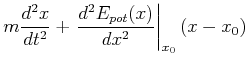 |
|||
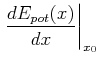 |
(8.816) |
geschrieben werden. Die Frequenz für kleine Bewegungen ist
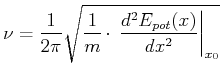 |
(8.817) |
Daraus folgt für die Periodendauer
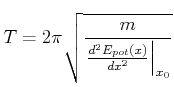 |
(8.818) |
(Siehe Tipler, Physik [Tip94, pp. 401]) (Siehe Gerthsen, Physik [Mes04, pp. 150])
Eine genaue Beobachtung zeigt, dass die Amplitude jeder freie Schwingung sich nach einer gewissen, charakteristischen Zeit um einen bestimmten Betrag erniedrigt. Die Dämpfung ist in vielen Fällen proportional zur Geschwindigkeit
| (8.819) |
Das Kräftegleichgewicht ergibt
Für kleine Dämpfungen ist die neue Resonanzfrequenz ![]() in der Nähe von
in der Nähe von ![]() . Mit jeder
Schwingung nimmt die Energie
. Mit jeder
Schwingung nimmt die Energie
![]() in einer definierten Zeiteinheit um einen bestimmten Betrag ab. Diese Leistung ist
in einer definierten Zeiteinheit um einen bestimmten Betrag ab. Diese Leistung ist
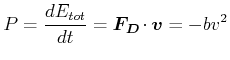 |
(8.821) |
Wenn wir ![]() durch
durch
![]() ersetzt, bekommt man
ersetzt, bekommt man
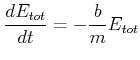 |
(8.822) |
Der Energieinhalt eines gedämpften Oszillators nimmt also exponentiell ab. Die relative Abnahme der Energie ist für alle Zeiten gleich. Wir lösen die Gleichung durch
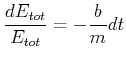 |
(8.823) |
und erhalten nach der Integration
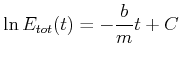 |
(8.824) |
oder, nach einer Exponentiation
| (8.825) |
Wir haben ![]() gesetzt. Mit der Zeitkonstante
gesetzt. Mit der Zeitkonstante
![]() bekommen wir
bekommen wir
| (8.826) |
|
|
Der Energieverlust pro Periode ![]() ist
ist
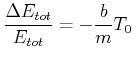 |
(8.827) |
Man charakterisiert die Dämpfung eines schwingungsfähigen Systems oft durch die Güte ![]() . Wenn der
Energieverlust pro Periode
. Wenn der
Energieverlust pro Periode
![]() ist, gilt
ist, gilt
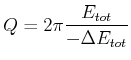 |
(8.828) |
Der ![]() -Faktor ist umgekehrt proportional zum relativen Energieverlust pro Periode
-Faktor ist umgekehrt proportional zum relativen Energieverlust pro Periode
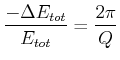
Es gilt auch
Da die Energie des Oszillators proportional zum Quadrat der Amplitude ist (
![]() gilt für die Abnahme der Amplitude
gilt für die Abnahme der Amplitude
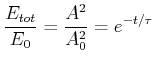 |
(8.830) |
Also ist
| (8.831) |
Zur Lösung der Schwingungsgleichung machen wir den komplexen Ansatz
| 0 | 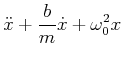 |
|||
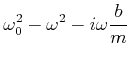 |
Dies ist eine quadratische Gleichung in ![]() . Die Lösungen sind
. Die Lösungen sind
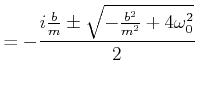 |
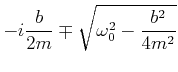 |
Es gibt drei Lösungen
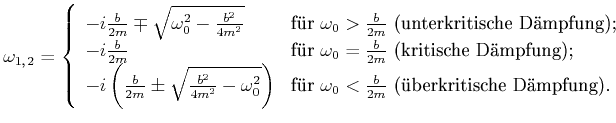 |
(8.832) |
Bei
![]() haben wir bis jetzt nur eine Lösung. In den anderen Fällen haben wir
jeweils das
haben wir bis jetzt nur eine Lösung. In den anderen Fällen haben wir
jeweils das ![]() .
.
Die entsprechenden Lösungsfunktionen sind
Wir testen noch, dass für
![]() die Lösung stimmt. Für diesen
Spezialfall lautet die Differentialgleichung
die Lösung stimmt. Für diesen
Spezialfall lautet die Differentialgleichung
| 0 |
Die Lösung der Schwingungsgleichung für den gedämpften Oszillator im Falle der unterkritischen Dämpfung ist
Wenn die Dämpfung den kritischen Wert
![]() übertrifft, schwingt das System nicht mehr. Für
übertrifft, schwingt das System nicht mehr. Für ![]() nennt man das System kritisch gedämpft. Für
nennt man das System kritisch gedämpft. Für ![]() ist es überkritisch gedämpft und für
ist es überkritisch gedämpft und für ![]() unterkritisch gedämpft.
unterkritisch gedämpft.
Zum Beispiel verwendet man in Autos geschwindigkeitsproportionale Stossdämpfer um eine kritische Dämpfung zu erreichen. Sind die Stossdämpfer alt, wird die Dämpfung der Fahrzeugschwingungen, z.B. durch Bodenwellen angeregt, unterkritisch und man fliegt von der Strasse.
(Siehe Tipler, Physik [Tip94, pp. 406]) (Siehe Gerthsen, Physik [Mes04, pp. 154])
![\includegraphics[width=0.12\textwidth]{schwingung-getriebenes-pendel}](img3275.gif)
|
|
|
Das vorliegende System wird durch zwei Grössen charakterisiert: die Anregungsschwingung
![]() sowie durch das Federpendel mit der Masse
sowie durch das Federpendel mit der Masse ![]() , der Dämpfung
, der Dämpfung ![]() und die Federkonstante
und die Federkonstante ![]() . Die
rücktreibende Kraft an der Feder ist
. Die
rücktreibende Kraft an der Feder ist
| (8.835) |
Die Beschleunigung ist wieder durch
![]() gegeben; die geschwindigkeitsproportionale
Dämpfung durch
gegeben; die geschwindigkeitsproportionale
Dämpfung durch
![]()
Die Bewegungsgleichung ist also
| (8.836) |
Wenn wir ![]() einsetzten und umstellen, erhalten wir
einsetzten und umstellen, erhalten wir
| (8.837) |
Wir teilen durch ![]() und kürzen
und kürzen
![]() ab und erhalten
ab und erhalten
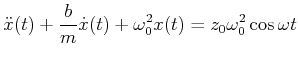 |
(8.838) |
Die Lösung (Simulation) dieser Gleichung besteht aus zwei Teilen: dem Einschwingvorgang als Lösung der Gleichung
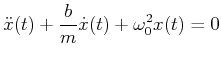
(analog zur freien gedämpften Schwingung, dieser Teil klingt ab gegen 0) sowie der stationären Lösung. Dieser Teil der Lösung hat die Form
| (8.839) |
wobei wir hier ein Minuszeichen vor der Phase setzen, damit diese die Phasendifferenz zur Anregung darstellt. Eingesetzt in die Bewegungsgleichung erhalten wir
![$\displaystyle A(\omega)\left[-\omega^2 \cos(\omega t -\delta(\omega)) -\frac{b}...
...in(\omega t
-\delta(\omega)) + \omega_0^2\cos(\omega t - \delta(\omega))\right]$](img3286.gif) |
|||
| (8.840) |
Um die Gleichung zu lösen müssen wir die Winkelfunktionen ![]() und
und ![]() mit Phasen in reine Winkelfunktionen
auflösen. Also setzen wie
mit Phasen in reine Winkelfunktionen
auflösen. Also setzen wie
![]() und
und
![]() . Wir bekommen dann
. Wir bekommen dann
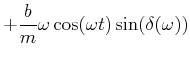 |
|||
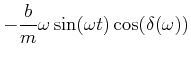 |
|||
| (8.841) |
Diese Gleichungen können vereinfacht werden
![$\displaystyle A(\omega)\left[-\omega^2 \cos(\delta(\omega))
+\frac{b}{m}\omega\sin(\delta(\omega))
+ \omega_0^2\cos(\delta(\omega))\right]$](img3299.gif) |
|||
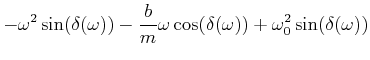 |
(8.842) |
Aus der zweiten Gleichung folgt
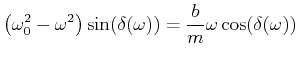 |
(8.843) |
und daraus
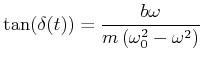 |
(8.844) |
Wir verwenden
![]() und
und
![]() und bekommen aus der ersten Gleichung
und bekommen aus der ersten Gleichung
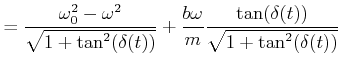 |
||
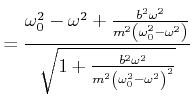 |
||
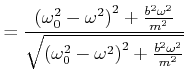 |
||
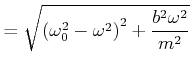 |
(8.845) |
Zusammengefasst ist die stationäre Lösung durch die Amplitude und Phase
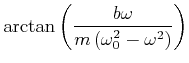 |
(8.846) | ||
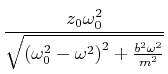 |
(8.847) |
Mit der Definition der Güte aus Gleichung (8.54) sowie mit
![]() schreiben wir
zuerst
schreiben wir
zuerst
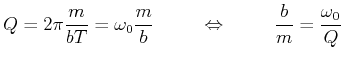 |
(8.848) |
und erhalten
|
Die folgenden Bilder zeigen einige typische Frequenz- und Phasengänge.
![\includegraphics[width=0.6\textwidth]{harmoisch-gedaempft1000}](img3318.gif)
Amplitude und Phase eines getriebenen harmonischen Oszillators mit
|
![\includegraphics[width=0.6\textwidth]{harmoisch-gedaempft200}](img3319.gif)
Amplitude und Phase eines getriebenen harmonischen Oszillators mit
|
![\includegraphics[width=0.6\textwidth]{harmoisch-gedaempft50}](img3320.gif)
Amplitude und Phase eines getriebenen harmonischen Oszillators mit
|
![\includegraphics[width=0.6\textwidth]{harmoisch-gedaempft10}](img3321.gif)
Amplitude und Phase eines getriebenen harmonischen Oszillators mit
|
Noch kompakter ist die folgende Schreibweise für die Amplitude
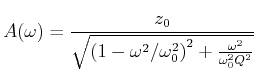 |
(8.851) |
Die Frequenz, bei der die Amplitude maximal wird, also die
Resonanzfrequenz, erhält man, indem man
![]() berechnet.
berechnet.
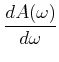 |
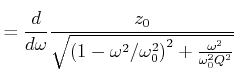 |
|||
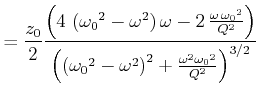 |
0 |
| 0 | 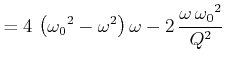 |
|
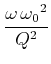 |
||
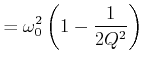 |
||
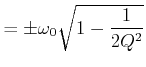 |
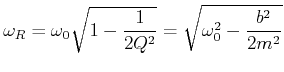 |
(8.852) |
Diese Resonanzfrequenz) ist kleiner als die Eigenfrequenz eines ungedämpften Systems (Siehe Gleichung (8.59) ).
Die Bestimmung der Kenndaten eines Oszillators aus der Amplitude ist bei hohen
Güten ![]() sehr schwierig und sehr ungenau. Viel einfacher ist es, die Phase bei
sehr schwierig und sehr ungenau. Viel einfacher ist es, die Phase bei
![]() und ihre Steigung an der Stelle zu bestimmen.
und ihre Steigung an der Stelle zu bestimmen.
Berechnung der Steigung
![]() :
:
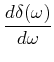 |
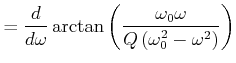 |
|
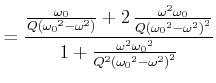 |
||
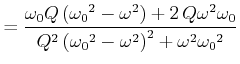 |
An der Stelle
![]() ist der Funktionswert
ist der Funktionswert
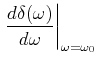 |
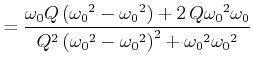 |
|||
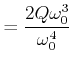 |
(Siehe Gerthsen, Physik [Mes04, pp. 142])
Wenn in der ![]() -Richtung eine Schwingung
-Richtung eine Schwingung
![]() und in der
und in der ![]() -Richtung eine Schwingung
-Richtung eine Schwingung
![]() überlagert werden, entstehen Lissajous-Figuren. Solche Schwingungen können
entstehen, wenn zum Beispiel eine Kugel in einer elliptischen Potentialmulde hin- und herschwingt.
überlagert werden, entstehen Lissajous-Figuren. Solche Schwingungen können
entstehen, wenn zum Beispiel eine Kugel in einer elliptischen Potentialmulde hin- und herschwingt.
![\includegraphics[width=0.7\textwidth]{schwingungen-ueberlagerung}](img3350.gif)
Zeigerdiagramm. Links für zwei Zeiten, in der Mitte das Zeigerdiagramm für zwei
Schwingungen (rot) und (blau) mit der Summe (grün) und rechts die Winkel.
|
Eine Schwingung
![]() kann durch einen Zeiger dargestellt werden. Die Projektion
dieses Zeigers auf die x-Achse ergibt das Schwingungsbild.
kann durch einen Zeiger dargestellt werden. Die Projektion
dieses Zeigers auf die x-Achse ergibt das Schwingungsbild.
Wenn zwei Schwingungen unterschiedlicher Amplitude und Phase, aber gleicher Frequenz addiert werden, kann man die trigonometrischen Sätze für schiefwinklige Dreiecke anwenden. So ist nach dem Cosinussatz
| (8.855) |
oder
 |
(8.856) |
Der Sinussatz liefert
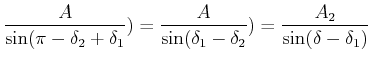 |
(8.857) |
Wenn wir die Zeit zur Berechnung so wählen, dass
![]() ist, so ergibt sich
ist, so ergibt sich
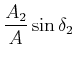 |
|||
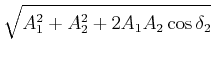 |
(8.858) |
|
|
Die Frequenzen der beiden Schwingungen sollen um
![]() verschieden sein. Wir setzen an
verschieden sein. Wir setzen an
| (8.859) |
Die resultierende Schwingung ist
| (8.860) |
Wir rechnen nun wie folgt um
Dies entspricht einer Schwingung der Frequenz ![]() mit einer aufmodulierten Frequenz
mit einer aufmodulierten Frequenz
![]() . Wir nennen diese verhalten auch Schwebung. Transparenter wird die Rechnung, wenn komplexe
Zahlen verwendet werden. Anstelle von
. Wir nennen diese verhalten auch Schwebung. Transparenter wird die Rechnung, wenn komplexe
Zahlen verwendet werden. Anstelle von
![]() schreiben wir
schreiben wir
![]() , wobei
wieder
, wobei
wieder
![]() ist. Wir schreiben
ist. Wir schreiben
| (8.862) |
und weiter
| (8.863) |
(Siehe Gerthsen, Physik [Mes04, pp. 146])
Die obige Schwingung ist nicht nur durch den zeitlichen Verlauf, sondern auch durch das Frequenzspektrumsowie das Phasenspektrum charakterisiert. Grundlage für diese Aussage ist der mathematische Satz, dass sich
jede periodische Funktion
![]() (Frequenz
(Frequenz
![]() als Fourierreihe
als Fourierreihe
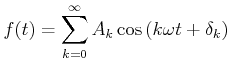 |
(8.864) |
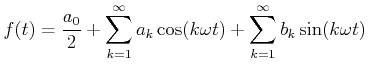 |
(8.865) |
Für gerade Funktionen
![]() sind alle
sind alle ![]() , für ungerade Funktionen sind alle
, für ungerade Funktionen sind alle ![]() .
.
|
|
|
|
![\includegraphics[width=0.7\textwidth]{schwingung_fourier_synth}](img3383.gif)
Synthese einer Schwingung mit
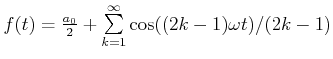 . Die verschiedenen Stufen der Synthese sind durch eine der Stufennummer proportionale
Verschiebung nach oben auseinandergezogen. . Die verschiedenen Stufen der Synthese sind durch eine der Stufennummer proportionale
Verschiebung nach oben auseinandergezogen.
|
![\includegraphics[width=0.7\textwidth]{schwingung_fourier_synth_1}](img3385.gif)
Synthese einer Schwingung mit
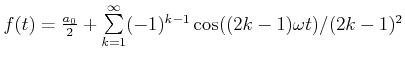 . Die verschiedenen Stufen der Synthese sind durch eine der Stufennummer
proportionale Verschiebung nach oben auseinandergezogen. . Die verschiedenen Stufen der Synthese sind durch eine der Stufennummer
proportionale Verschiebung nach oben auseinandergezogen.
|
![\includegraphics[width=0.7\textwidth]{schwingung_fourier_synth_2}](img3387.gif)
Synthese einer Schwingung mit
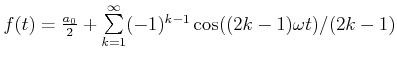 . Die verschiedenen Stufen der Synthese sind durch eine der Stufennummer
proportionale Verschiebung nach oben auseinandergezogen. . Die verschiedenen Stufen der Synthese sind durch eine der Stufennummer
proportionale Verschiebung nach oben auseinandergezogen.
|
![\includegraphics[width=0.7\textwidth]{schwingung_fourier_synth_3}](img3389.gif)
Synthese einer Schwingung mit
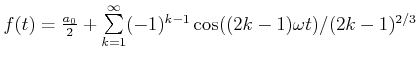 . Die verschiedenen Stufen der Synthese sind durch eine der
Stufennummer proportionale Verschiebung nach oben auseinandergezogen. . Die verschiedenen Stufen der Synthese sind durch eine der
Stufennummer proportionale Verschiebung nach oben auseinandergezogen.
|
![\includegraphics[width=0.7\textwidth]{schwingung_fourier_synth_4}](img3391.gif)
Synthese einer Schwingung mit
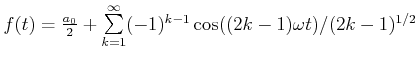 . Die verschiedenen Stufen der Synthese sind durch eine der
Stufennummer proportionale Verschiebung nach oben auseinandergezogen. . Die verschiedenen Stufen der Synthese sind durch eine der
Stufennummer proportionale Verschiebung nach oben auseinandergezogen.
|
![\includegraphics[width=0.7\textwidth]{schwingung_fourier_synth_5}](img3393.gif)
Synthese einer Schwingung mit
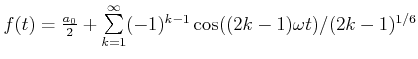 . Die verschiedenen Stufen der Synthese sind durch eine der
Stufennummer proportionale Verschiebung nach oben auseinandergezogen. . Die verschiedenen Stufen der Synthese sind durch eine der
Stufennummer proportionale Verschiebung nach oben auseinandergezogen.
|
Die folgenden Applets illustrieren die Fourieranalyse und -synthese
(Siehe Gerthsen, Physik [Mes04, pp. 181])
![\includegraphics[width=0.8\textwidth]{schwingung-gekoppelte-Pendel}](img3395.gif)
Zwei mathematische Pendel im Abstand
|
|
|
Wenn das linke Pendel um ![]() und das rechte Pendel um
und das rechte Pendel um ![]() ausgelenkt wird (in beiden
Fällen wird nach rechts positiv gezählt), dann verändert sich die Länge der Feder um
ausgelenkt wird (in beiden
Fällen wird nach rechts positiv gezählt), dann verändert sich die Länge der Feder um
| (8.866) |
| (8.867) |
| (8.868) |
| (8.869) |
| (8.870) |
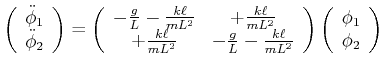 |
(8.872) |
Wir nehmen an, dass beide Pendel mit der gleichen Frequenz ![]() schwingen. Wir setzen also
an
schwingen. Wir setzen also
an
| (8.873) |
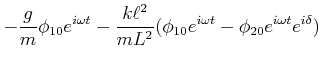 |
|||
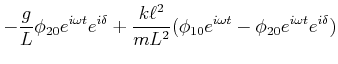 |
(8.874) |
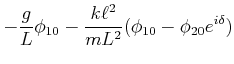 |
|||
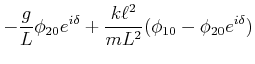 |
(8.875) |
![$\displaystyle \left[-\omega^2+\frac{g}{L}+\frac{k\ell^2}{mL^2}\right]\phi_{1,0}-\frac{k\ell^2}{mL^2}\phi_{2,0}e^{i\delta}$](img3431.gif) |
|||
![$\displaystyle - \frac{k\ell^2}{mL^2}\phi_{1,0}+\left[-\omega^2 +\frac{g}{L} +\frac{k\ell^2}{mL^2}\right]\phi_{2,0}e^{i\delta}$](img3432.gif) |
(8.876) |
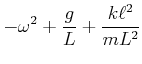 |
|||
| (8.877) |
| (8.878) |
| (8.879) |
| (8.880) |
| (8.881) |
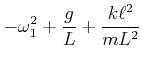 |
|||
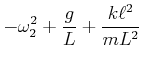 |
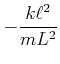 |
(8.882) |
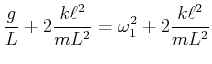 |
(8.883) |
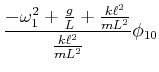 |
|||
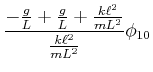 |
|||
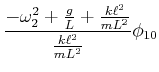 |
|||
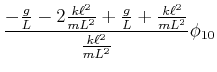 |
|||
| (8.884) |
(Siehe Gerthsen, Physik [Mes04, pp. 181])
|
|
Wir wollen nun untersuchen, wie die Lösung der Schwingungsgleichung für ![]() gleich Pendel
aussieht, die jeweils vom
gleich Pendel
aussieht, die jeweils vom ![]() -ten zum
-ten zum ![]() -ten Pendel mit einer masselosen Feder mit der
Federkonstante
-ten Pendel mit einer masselosen Feder mit der
Federkonstante ![]() gekoppelt sind. Für das erste Pendel mit
gekoppelt sind. Für das erste Pendel mit ![]() gilt
gilt
| (8.885) |
| (8.886) |
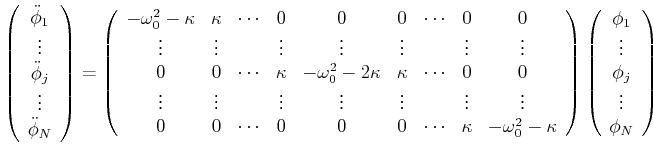 |
(8.888) |
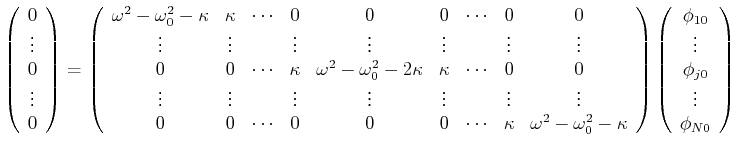 |
(8.889) |
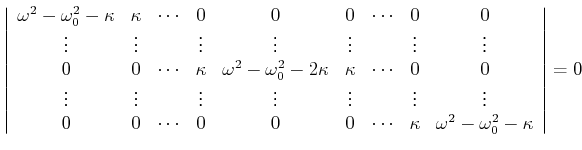 |
(8.890) |
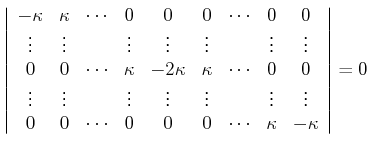 |
(8.891) |
Othmar Marti