Weiter: Rechnen mit Vektoren Oben: Vorlesungsskript Klassische und relativistische Zurück: Berechnungen in ebenen schiefwinkligen Skript: PDF-Datei Übungen: Blätter ILIAS: Materialien Korrekturen
Dieser Text bezieht sich auf den Abschnitt 5.2.3. Hier wird ein Beispiel gerechnet. Der Maple Quelltext ist:
> with(LinearAlgebra): > with(VectorCalculus): > with(tensor): > SetCoordinates( 'cartesian'[x,y,z] ): > > > AA := Matrix(3,3,[[cos(omegaz*t), sin(omegaz*t),0], > [-sin(omegaz*t),cos(omegaz*t),0], > [0,0,1]]); > > AAinv := MatrixInverse(AA); > omega := <0,0,omegaz>; > s := <R*cos(3*omegaz*t),R*sin(3*omegaz*t),rz>; > sp := convert(MatrixVectorMultiply(AA,s),arctrig); > res1 :=diff(s,t); > CrossProduct(omega,s); > tr1 :=diff(sp,t); > tr2 := simplify(MatrixVectorMultiply(AAinv,tr1)); > res2 := tr2+CrossProduct(omega,s); > rr :=simplify(res2-res1); >
Hier ist angenommen worden, dass der Rotationsvektor
![]() entlang der
entlang der ![]() -Richtung des
Koordinatensystems angeordnet ist. Dann transformiert die Matrix
-Richtung des
Koordinatensystems angeordnet ist. Dann transformiert die Matrix ![]() einen Vektor aus dem Laborsystem in das
rotierende Bezugssystem.
einen Vektor aus dem Laborsystem in das
rotierende Bezugssystem. ![]() transformiert zurück.
transformiert zurück. ![]() ist der zeitabhängige Ortsvektor.
ist der zeitabhängige Ortsvektor. ![]() ist der
Ortsvektor transformiert in das rotierende Bezugssystem.
ist der
Ortsvektor transformiert in das rotierende Bezugssystem. ![]() ist die Ableitung von
ist die Ableitung von ![]() im rotierenden
Bezugssystemm
im rotierenden
Bezugssystemm ![]() ist
ist ![]() zurücktransformiert in das Laborsystem.
zurücktransformiert in das Laborsystem.
Gleichung (5.17) gilt dann, wenn die Ableitung im rotierenden Bezugssystem zurück nach dem Laborsystem transformiert ist.
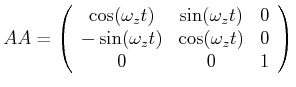
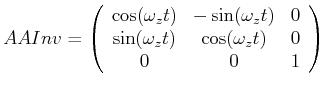
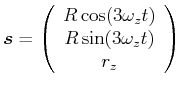
Nach Umformung erhält man
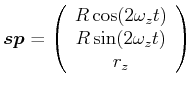
im rotierenden Bezugssystem.
Die Ableitungen sind
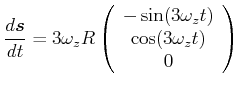
und
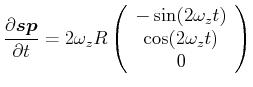
im gestrichenen Bezugssystem. Zurücktransformiert erhält man
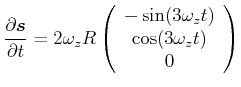
Das Kreuzprodukt ist
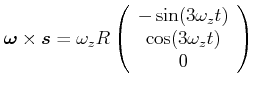
so dass
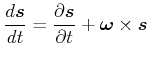
gilt.
Othmar Marti