Weiter: Spezielle Relativitätstheorie Oben: Relativität Zurück: Klassische Relativität gleichförmig bewegter Skript: PDF-Datei Übungen: Blätter ILIAS: Materialien Korrekturen
![]() ,
, ![]() ,
,![]() ,
,![]() sei gegen das Inertialsystem
sei gegen das Inertialsystem ![]() ,
,![]() ,
,![]() ,
,![]() mit
mit
![]() beschleunigt. Dier
Trägheitsbeschleunigung
beschleunigt. Dier
Trägheitsbeschleunigung ![]() ist durch
ist durch
Wir fordern: Massen und Zeiten sollen in beiden Systemen gleich sein.
Die Gesetze der Mechanik sollen in beiden Systemen die gleiche Form haben.
| (5.430) | ||
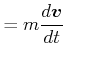 |
(5.431) | |
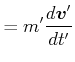 |
(5.432) |
Dabei ist
![]() . Die Differenz nennen wir eine Trägheitskraft:
. Die Differenz nennen wir eine Trägheitskraft:
![]() ,
,
also
| (5.433) |
![]() ist die Kraft, die einen nach hinten drückt.
ist die Kraft, die einen nach hinten drückt.
Beweis:
| (5.434) |
Beispiel: Schwerelosigkeit im fallenden Aufzug
Behauptung
| (5.435) |
|
|
Wir wollen das folgende Problem Lösen:
Ein System von Massenpunkten ![]() bewegt sich unter Einfluss externer Kräfte
bewegt sich unter Einfluss externer Kräfte
![]() und interner Kräfte
und interner Kräfte
![]() . Es gibt deshalb äusserst komplexe Bewegungsgleichungen.
. Es gibt deshalb äusserst komplexe Bewegungsgleichungen.
Prinzip: Ersetzt man die Beschleunigung
![]() der Masse
der Masse ![]() durch die Trägheitskraft
durch die Trägheitskraft
| (5.436) |
so wird das Problem der Dynamik auf ein statisches Problem zurückgeführt.
Situation für einen ruhenden Beobachter
![\includegraphics[width=0.25\textwidth]{relativ-002}](img1579.gif)
Situation für einen ruhenden Beobachter
|
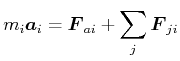
ist die Gleichung, die das System aus der Dynamik beschreibt.
![\includegraphics[width=0.4\textwidth]{relativ-003}](img1581.gif)
Situation für einen mitbewegten Beobachter
|
Nach dem Prinzip von d'Alembert gilt
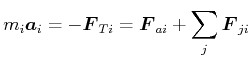 |
(5.437) |
oder
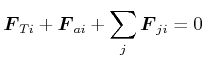 |
(5.438) |
Trägheitskräfte: Zentrifugalkraft und Corioliskraft
![]() ,
,![]() ,
,![]() ,
,![]() sei Inertialsystem
sei Inertialsystem
![]() ,
,![]() ,
,![]() ,
,![]() rotiert um
rotiert um ![]() , Nullpunkte sind identisch.
, Nullpunkte sind identisch.
Winkelgeschwindigkeitsvektor
![]()
![\includegraphics[width=0.4\textwidth]{relativ-004}](img1586.gif)
Winkelgeschwindigkeitsvektor
|
Wir betrachten einen beliebigen Vektor
![]() . Dieser Vektor ändere sich um
. Dieser Vektor ändere sich um
![]() . Diese Änderung
kann in eine durch die gleichförmige Rotation bedingte Komponente
. Diese Änderung
kann in eine durch die gleichförmige Rotation bedingte Komponente
![]() und in eine Komponente
im gleichförmig rotierenden gestrichenen Koordinatensystem
und in eine Komponente
im gleichförmig rotierenden gestrichenen Koordinatensystem
![]() (relative Änderung)
aufgeteilt werden.
(relative Änderung)
aufgeteilt werden.
Wir betrachten das Dreieck ![]() und erhalten
und erhalten
![]() ist tangential und steht damit senkrecht auf
ist tangential und steht damit senkrecht auf
![]() . Als Tangentenvektor liegt
. Als Tangentenvektor liegt
![]() in der Ebene
senkrecht zu
in der Ebene
senkrecht zu
![]() . Also zeigt
. Also zeigt
![]() in die
gleiche Richtung wie
in die
gleiche Richtung wie
![]() . Da
. Da
![]() ist, gilt auch
ist, gilt auch
daraus folgt
Wir verwenden im folgenden die Notation, um die Ableitungen im gestrichenen und ungestrichenen Koordinatensystem unterscheiden zu können:
|
wobei ![]() und
und ![]() sein soll.
sein soll.
Also erhalten wir
Wichtig ist, dass
![]() die im rotierenden Koordinatensystem durchgeführte
Ableitung ist, aber wieder zurücktransformiert in das lokale Koordinatensystem (siehe auch J).
die im rotierenden Koordinatensystem durchgeführte
Ableitung ist, aber wieder zurücktransformiert in das lokale Koordinatensystem (siehe auch J).
Beispiel:
Sei
![]() , so ist auch:
, so ist auch:
![]() ,
,
![]() und damit
und damit
| (5.440) |
Geschwindigkeiten (und auch Beschleunigungen) sind in den beiden Bezugssystemen nicht gleich, wohl aber Ortsvektoren. Diese haben zwar unterschiedliche Komponenten, zeigen aber immer auf den gleichen Punkt im Raum. Geschwindigkeiten und Beschleunigungen sind unterschiedlich, haben also eine unterschiedliche Länge und/oder eine unterschiedliche Richtung.
Wir betrachten die Beschleunigung. Wir haben für die Beschleunigung im Laborsystem
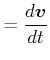 |
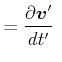 |
Dann ist
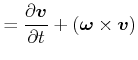 |
||
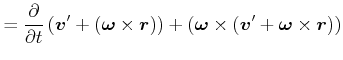 |
||
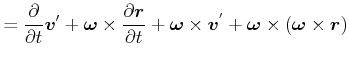 |
||
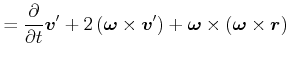 |
(5.441) |
also haben wir
| (5.442) |
In Gleichung (5.7) ist die Trägheitsbeschleunigung definiert. Wir setzen
| (5.443) |
Wir haben also
| (5.444) | ||||
| (5.445) |
Wir können die Gleichung für die vereinfachen, indem wir
wobei
![]() und
und
![]() sein soll.
sein soll.
![\includegraphics[width=0.4\textwidth]{relativ-005}](img1627.gif)
Lage von
|
Wir verwenden die Vektoridentität aus Gleichung (K.7)
Mit
![]() bekommen wir dann
bekommen wir dann
| (5.446) |
Also können wir die Bewegung durch Trägheitskräfte beschreiben
| (5.447) |
und
| (5.448) |
Die Trägheitskräfte sind
|
|
|
|
Die Zentrifugalkraft ist nur von der Position, nicht aber von der Geschwindigkeit ![]() im
gleichförmig rotierenden Bezugssystem abhängig. Die Corioliskraft andererseits hängt nur von
im
gleichförmig rotierenden Bezugssystem abhängig. Die Corioliskraft andererseits hängt nur von ![]() ab, aber
nicht von
ab, aber
nicht von ![]() .
.
![\includegraphics[width=0.7\textwidth]{relativ-006}](img1641.gif)
|
![\includegraphics[width=0.5\textwidth]{relativ-007}](img1642.gif)
|
mitbewegtes Koordinatensystem:
![]() : nach E
: nach E
![]() : nach N
: nach N
![]() : nach oben
: nach oben
![]()
![]()
![]() die geographische Breite.
die geographische Breite.
Die Winkelgeschwindigkeit ist im gestrichenen Bezugssystem
| (5.449) |
Der Vektor ![]() hat die Länge
hat die Länge
| (5.450) |
Im gestrichenen Bezugssystem hat ![]() die Koordinaten
die Koordinaten
| (5.451) |
| (5.452) |
oder betragsmässig
| (5.453) |
Die Komponente parallel zum Boden (also in der ![]() -Richtung ist
-Richtung ist
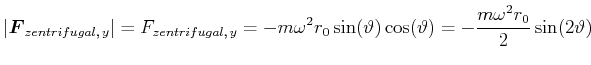 |
(5.454) |
Wenn ![]() die Relativgeschwindigkeit ist, gilt in
die Relativgeschwindigkeit ist, gilt in ![]() ,
,![]() ,
,![]() ,
,![]() für die Corioliskraft:
für die Corioliskraft:
![$\displaystyle \vec{F}_{coriolis}=2m\omega\left( \begin{array}[c]{c} v_{x}' v...
...cos\vartheta -v_{x}'\sin\vartheta v_{x}'\cos\vartheta \end{array} \right)$](img1654.gif) |
(5.455) |
|
|
![\includegraphics[width=0.3\textwidth]{relativ-008}](img1655.gif)
|
Das Foucault-Pendel ist an einem Punkt mit der Erde verbunden.
![]() projiziert auf
projiziert auf ![]() , dies entspricht der Drehgeschwindigkeit gegen
, dies entspricht der Drehgeschwindigkeit gegen ![]() ,
,![]() ,
,![]()
also
| (5.456) |
Rotationsperiode
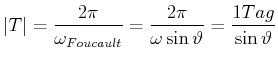 |
(5.457) |
![\includegraphics[width=\textwidth]{relativ-009}](img1659.gif)
Erde und Mond
|
|
Schwerpunkt des Systems Erde-Mond:
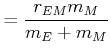 |
||
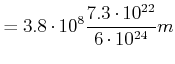 |
||
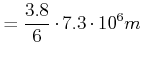 |
||
| (5.458) |
Erde und Mond drehen sich um den gemeinsamen Schwerpunkt.
![\includegraphics[width=0.4\textwidth]{relativ-010}](img1671.gif)
|
Bezogen auf den Erdmittelpunkt herrscht die Gravitationskraft
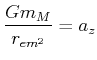
Weiter ist die Geschwindigkeit des Punktes ![]() bezogen auf die Geschwindigkeit
bezogen auf die Geschwindigkeit ![]() des Schwerpunktes
des Schwerpunktes ![]() gegeben
durch
gegeben
durch
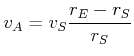
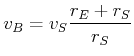
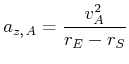
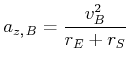
| Punkt |
Punkt |
|
| Feldvektor der Gravitation des Mondes |
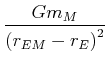
|
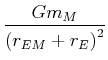
|
| Zentrifugalbeschleunigung |
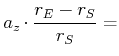
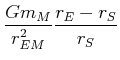
|
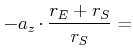

|
| Summe der Beschleunigungen |
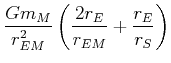
|
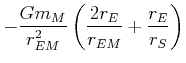
|
in ![]() gibt es die Zentrifugalbeschleunigung
gibt es die Zentrifugalbeschleunigung
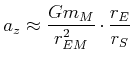
Zwischen ![]() und
und ![]() sowie
sowie ![]() gibt es die Differenz der Beschleunigungen
gibt es die Differenz der Beschleunigungen
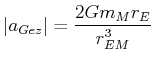 |
(5.459) |
Vergleich mit ![]()
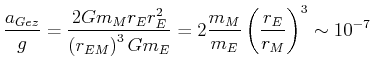 |
(5.460) |
Anwendung Schwerkraft in einem Raumschiff
![\includegraphics[width=0.8\textwidth]{relativ-011}](img1692.gif)
Schwerkraft in einem Raumschiff
|
Nur im Schwerpunkt ist die Zentrifugalkraft gleich der Gravitationskraft
in ![]() ist die Gravitation zu gross
ist die Gravitation zu gross
in ![]() ist die Gravitation zu klein
ist die Gravitation zu klein
![\includegraphics[width=0.3\textwidth]{relativ-012}](img1693.gif)
Schwerkraft in einem Raumschiff in radialer Richtung
|
Im Raumschiff ist die Gravitationskraft nicht Null.
Othmar Marti