Weiter: Scherung Oben: Skalare Elastomechanik Zurück: Skalare Elastomechanik  Skript:  PDF-Datei Übungen:  Blätter

Dehnung und Kompression

Dieser Stoff wurde am 4.12.2001 behandelt

(Siehe Tipler, Physik[Tip94, 342]) (Siehe Gerthsen, Physik[GV95, 130])

Zieht man an einem Draht (Länge $\ell$, Querschnitt $d$ und Querschnittsfläche $A=\frac{\pi}{4}d^2$), dann vergrössert sich die Länge um $\Delta \ell$ und verringert sich (meistens) der Querschnitt um $\Delta d$.

$$\Delta \ell = \epsilon\ell$$

$$-\Delta d = \mu\epsilon d$$ (5.358)

Es sind

• $\epsilon$ die relative Dehnung
• $\mu$ die Poisson-Zahl

Wir definieren nun die Spannung

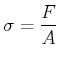$$\sigma = \frac{F}{A}$$ (5.359)

dabei ist $F$ die an der Querschnittsfläche $A$ wirkende Kraft.

Das Hooke'sche Gesetz verknüpft Spannung $\sigma$ und Dehnung $\epsilon$

$$\sigma = E \epsilon$$ (5.360)

$E$ ist eine Materialkonstante, der Elastizitäts- oder der Dehnungsmodul (im englischen Young's Modulus genannt).

Einheiten

• $\epsilon$: dimensionslos
• $\sigma$: $\frac{N}{m^2}$
• $E$: $\frac{N}{m^2}$

Wenn wir die obigen Gleichungen umschreiben, erhalten wir

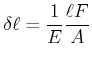$$\delta \ell = \frac{1}{E} \frac{\ell F}{A}$$ (5.361)

Aus Änderung des Querschnittes und der Länge können wir die Volumenänderung berechnen. Wir setzen an, dass $V = \ell d^2$ ist

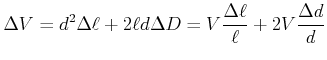$$\Delta V = d^2 \Delta \ell + 2 \ell d \Delta D = V \frac{\Delta \ell}{\ell} + 2 V \frac{\Delta d}{d}$$ (5.362)

Umgeschrieben erhalten wir

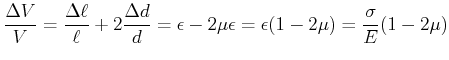$$\frac{\Delta V}{V} = \frac{\Delta \ell}{\ell} + 2 \frac{\Delta d}{d} = \epsilon - 2\mu\epsilon = \epsilon(1-2\mu) = \frac{\sigma}{E}(1-2\mu)$$ (5.363)

Wir sehen, dass für positives $\Delta V$ die Poisson-Zahl der Ungleichung $\mu \leq 0.5$ genügen muss. In speziellen fällen kann $\mu$ auch grösser als $0.5$ sein.

Wir haben hier $\sigma$ und $\epsilon$ als Skalare angenommen.

Wird der Testkörper hydrostatischem Druck $\Delta p$ unterworfen, ist also die Spannung auf allen Seiten gleich, ändert sich das Volumen um den dreifachen Wert, der bei einer uniaxialen Spannung auftreten würde.

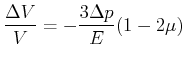$$\frac{\Delta V}{V} = - \frac{3 \Delta p}{E}(1-2\mu)$$ (5.364)

Die Kompressibilität $\kappa = \frac{\Delta V}{V\Delta p}$ ist

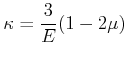$$\kappa = \frac{3}{E}(1-2\mu)$$ (5.365)

Wird ein Draht gedehnt, kann ihm die Federkonstante $k = \frac{\Delta F}{\Delta \ell} = \frac{A E}{\ell}$ zuschreiben.

Bei der Dehnung wird die Arbeit

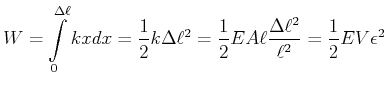$$W = \int\limits_0^{\Delta\ell} k x dx = \frac{1}{2} k \Delta\ell^2 = \frac{1}{2} E A \ell \frac{\Delta \ell^2}{\ell^2} = \frac{1}{2} E V \epsilon^2$$ (5.366)

verrichtet. Wenn wir die Arbeit, oder Energie, pro Volumeneinheit ausrechnen, ist die elastische Energiedichte

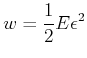$$w = \frac{1}{2}E\epsilon^2$$ (5.367)

 Skript:  PDF-Datei Übungen:  Blätter