Weiter: Schwingungen und Wellen Oben: Relativistische Mechanik Zurück: Relativität der Gleichzeitigkeit  Skript:  PDF-Datei Übungen:  Blätter

Unterabschnitte

• Vergleich der Lorentz-Transformation mit der Galilei-Transformation

Lorentz-Transformation

Dieser Stoff wurde am 8. 1. 2002 behandelt

(Siehe Tipler, Physik[Tip94, 1157]) (Siehe Gerthsen, Physik[GV95, 853])

Die im vorherigen Abschnitt besprochenen Transformationen der zeit und der Länge lassen sich in der sogenannten Lorentz-Transformation zusammenfassen.

Beschreibung eines Punktereignisses in zwei gegeneinander bewegten Bezugssystemen

Dieser Stoff wurde am 9. 1. 2001 behandelt

Materialien

Folien zur Vorlesung am 09. 01. 2002 PDF

Das Punktereignis $P$ soll im gestrichenen Koordinatensystem (B) sowie im ungestrichenen Koordinatensystem (A) ausgemessen werden.

• Jede Längeneinheit von B bringt A um $1/\sqrt{1-v^2/c^2}$ ihrer Einheiten nach rechts und um $(v/c)/\sqrt{1-v^2/c^2}$ in der ,,Zeitachse'' $ct$ nach oben.
• Jede ,,Zeiteinheit'' auf der $ct'$-Achse bringt A um $1/\sqrt{1-v^2/c^2}$ ,,Zeiteinheiten'' auf der $ct$-Achse nach oben und um $(v/c)/\sqrt{1-v^2/c^2}$ nach rechts.

Wenn wir die obigen Beobachtungen zusammenfassen, erhalten wir

$$x = \left(x'+ \frac{v}{c} \left(ct'\right)\right)\frac{1}{\sqrt{1-v^2/c^2}}$$

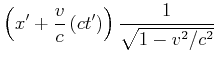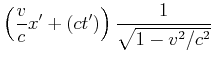$$ct = \left(\frac{v}{c} x' + \left(c t'\right)\right) \frac{1}{\sqrt{1-v^2/c^2}}$$ (7.427)

Wir rechnen nun nicht mehr mit $ct$ sondern mit der Zeit $t$ direkt und erhalten die Lorentz-Transformation.

$$\begin{array}{ccc} x = \frac{x' + v t'}{\sqrt{1-v^2/c^2}} &\h... ...h} &t = \frac{v x' /c^2 + t'}{\sqrt{1-v^2/c^2}} \\ \end{array}$$ (7.428)

Die Lorentz-Transformation kann auch in Matrix-Schreibweise dargestellt werden:

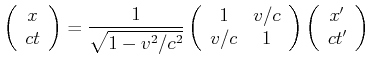$$\left(\begin{array}{c} x \\ ct \\ \end{array}\right) = \frac{1}... ...\\ \end{array}\right) \left(\begin{array}{c} x' \\ ct' \\ \end{array}\right)$$ (7.429)

Wir wissen, dass $\tan \alpha = v/c$ ist. Dann ist auch $1/\sqrt{1+v^2/c^2} = \cos\alpha$ und $\sin\alpha = \tan\alpha \cdot \cos\alpha = (v/c)/\sqrt{1+v^2/c^2}$. In einem gedrehten Koordinatensystem wäre

$$x = x' \cos\alpha + y'\sin\alpha$$

$$y = -x'\sin\alpha + y'\cos\alpha$$ (7.430)

Diese Rotation sieht unserer Lorentz-Transformation sehr ähnlich. Die Vorzeichen unter den Wurzeln beim Cosinus und beim Sinus stimmen nicht. Zudem werden bei der Lorentz-Transformation die Orts- und die Zeitachse in gegenläufiger Richtung verdreht.

Diese Diskrepanz kann aufgelöst werden, wenn man nicht $ct$ als Zeitachse verwendet, sondern $ict$, wobei $i=\sqrt{-1}$ die imaginäre Einheit ist. In einem Raum mit den Koordinaten $(x;\,y;\,z;\,ict)$ ist die Lorentz-Transformation nichts anderes als eine Rotation des Koordinatensystems.

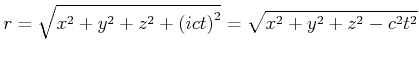Wenn wir, analog zum klassischen dreidimensionalen Raum ( $r = \sqrt{x^2+y^2+z^2}$) den Abstand $r = \sqrt{x^2+y^2+z^2+\left(ict\right)^2} = \sqrt{x^2+y^2+z^2-c^2t^2}$ definieren, haben wir eine, vom jeweiligen Koordinatensystem unabhängige Definition des Abstandes. Dieser sogenannte Viererabstand ist unabhängig vom Koordinatensystem, sofern die einzelnen Koordinatensysteme mit der Lorentz-Transformation ineinander übergeführt werden können. Ein Punktereignis wird in dieser Sprache mit einem Vierervektor beschrieben.

Vergleich der Lorentz-Transformation mit der Galilei-Transformation

Grösse	Galilei-Transformation	Lorentz-Transformation
	klassische Physik	relativistische Physik
Ortskoordinaten	$x;\,y;\,z$	$x;\,y;\,z$
Zeitkoordinaten	$t$	$ict$
Länge	$x = x' + v t'$	$x = \frac{x' + v t'}{\sqrt{1-v^2/c^2}}$
Zeit	$t = t'$	$t = \frac{v x' /c^2 + t'}{\sqrt{1-v^2/c^2}}$
Abstand	$r = \sqrt{x^2+y^2+z^2}$	$r = \sqrt{x^2+y^2+z^2-c^2t^2}$

 Skript:  PDF-Datei Übungen:  Blätter