![\includegraphics[width=0.7\textwidth]{gleichzeitigkeit.eps}](img1213.gif)
Die zwei Novae sollen an den angegebenen Orten und Zeiten ausbrechen. ''B'' befindet sich
in einem Inertialsystem, das sich mit der Geschwindigkeit ![]() gegenüber meinem
Inertialsystem bewegt.
gegenüber meinem
Inertialsystem bewegt.
| Dieser Stoff wurde am 11.12.2001 behandelt |
![\includegraphics[width=0.7\textwidth]{gleichzeitigkeit.eps}](img1213.gif)
Die zwei Novae sollen an den angegebenen Orten und Zeiten ausbrechen. ''B'' befindet sich
in einem Inertialsystem, das sich mit der Geschwindigkeit
|
In der Abbildung stellt die horizontale Achse alle drei Raumkoordinaten zusammen dar. Am
Ort ![]() befinde ich mich. Deshalb ist die Zeitachse mein ''hier''. Andererseits haben
alle Punkte auf der ''r''-Achse die gleich Zeit wie ich, sie befinden sich also jetzt.
Das hier und jetzt eines sich in einem mit der Geschwindigkeit
befinde ich mich. Deshalb ist die Zeitachse mein ''hier''. Andererseits haben
alle Punkte auf der ''r''-Achse die gleich Zeit wie ich, sie befinden sich also jetzt.
Das hier und jetzt eines sich in einem mit der Geschwindigkeit ![]() gegenüber meinem
Inertialsystem bewegenden Beobachter B sind gekippt gegenüber meinen Koordinatenachsen. B
soll gleichzeitig die Explosion von je einer Nova links und rechts von ihm beobachten.
Beide Novae sollen den gleichen Abstand von B haben. Sie sollen, als B's Weltlinie die
meinige kreuzte ausgebrochen sein
gegenüber meinem
Inertialsystem bewegenden Beobachter B sind gekippt gegenüber meinen Koordinatenachsen. B
soll gleichzeitig die Explosion von je einer Nova links und rechts von ihm beobachten.
Beide Novae sollen den gleichen Abstand von B haben. Sie sollen, als B's Weltlinie die
meinige kreuzte ausgebrochen sein
Dies kann wie folgt eingesehen werden:
Die beiden roten Achsen unter ![]() stellen die Ausbreitung des Lichtes dar: die
Lichtgeschwindigkeit bei unserer Wahl der Koordinaten ist 1. Die beiden roten Linien
durch die beiden Ereignisse zeigen, dass B beide Novae gleichzeitig wahrnimmt. Ich
hingegen sehe zuerst die Nova 1, dann die Nova 2, da der Schnittpunkt der ersten roten
Linie mit der ct-Achse unter dem der zweiten Linie liegt.
stellen die Ausbreitung des Lichtes dar: die
Lichtgeschwindigkeit bei unserer Wahl der Koordinaten ist 1. Die beiden roten Linien
durch die beiden Ereignisse zeigen, dass B beide Novae gleichzeitig wahrnimmt. Ich
hingegen sehe zuerst die Nova 1, dann die Nova 2, da der Schnittpunkt der ersten roten
Linie mit der ct-Achse unter dem der zweiten Linie liegt.
| Der Begriff der Gleichzeitigkeit hängt vom betrachteten Inertialssystem ab. |
Durch die Wahl der Geschwindigkeit von B ist der Winkel ![]() zwischen meiner ct-Achse
und der von B festgelegt. Was ist der Winkel zwischen B's r-Achse und meiner? Der Kreis
um den Ursprung geht sowohl durch B's Beobachtung wie auch durch die beiden Novae.
deshalb it das Dreieck gebildet durch die beiden Novae sowie B's Beobachtungszeitpunkt
rechtwinklig. Es ist also
zwischen meiner ct-Achse
und der von B festgelegt. Was ist der Winkel zwischen B's r-Achse und meiner? Der Kreis
um den Ursprung geht sowohl durch B's Beobachtung wie auch durch die beiden Novae.
deshalb it das Dreieck gebildet durch die beiden Novae sowie B's Beobachtungszeitpunkt
rechtwinklig. Es ist also
Da das Dreieck aus der Nova 2, B's Beobachtungszeitpunkt und dem Koordinatenursprung gleichschenklig ist, ist auch
Damit ist auch
Da die Winkel der beiden Lichtlinien zur ![]() -Achse beziehungsweise zur
-Achse beziehungsweise zur ![]() -Achse
-Achse ![]() sind, gilt auch
sind, gilt auch
Ebenso liest man aus dem Dreieck Nova 1, Ursprung und der Schnittstelle der Lichtgerade mit der r-Achse
Also ist
| (7.386) |
| Dieser Stoff wurde am 12.12.2001 behandelt |
Materialien
Folien zur Vorlesung am 12. 12. 2001 PDFText (nur von uni-ulm.de aus zu sehen)
Je schneller B ist, desto mehr werden, von mir aus gesehen, seine Achsen gegen die
![]() Linie gekippt.
Linie gekippt.
![\includegraphics[width=0.7\textwidth]{gleichzeitigkeit-B.eps}](img1226.gif)
Die beiden Novae aus der Sicht von B.
|
Die Beschreibung von B ist ebenso gültig. Aus seiner Sicht ist meine Geschwindigkeit
genau das negative von seiner, von mir aus gesehen. Deshalb ist mein ct-Achse um ![]() gegen den Uhrzeigersinn geneigt.
gegen den Uhrzeigersinn geneigt.
Ereignisse, die aus B's Sicht gleichzeitig sind, sind für mich nicht gleichzeitig, und umgekehrt.
| Relationen zwischen Ereignissen sind nur dann sinnvoll zu beschreiben, wenn gleichzeitig auch das Bezugssystem angegeben wird. |
| Dieser Stoff wurde am 12.12.2001 behandelt |
![\includegraphics[width=0.7\textwidth]{massstabsvergleich.eps}](img1227.gif)
Massstabsvergleich
|
Die beiden Koordinatenursprünge (B's und meiner) sollen übereinander liegen. Zum
Zeitpunkt ![]() (gilt für beide) ist das linke Ende je eines Massstabes genau am
Ursprung. Das Ende meines Massstabes ist in
(gilt für beide) ist das linke Ende je eines Massstabes genau am
Ursprung. Das Ende meines Massstabes ist in ![]() und bewegt sich weiter zu
und bewegt sich weiter zu ![]() . Das
rechte Ende von B's Massstab beschreibt die Linie
. Das
rechte Ende von B's Massstab beschreibt die Linie ![]() nach
nach ![]() . Für mich ist zur Zeit
. Für mich ist zur Zeit
![]() das Ende von B's Massstab in
das Ende von B's Massstab in ![]() , für ihn ist es in
, für ihn ist es in ![]() . Analog sagt B, dass mein
Massstab zur Zeit
. Analog sagt B, dass mein
Massstab zur Zeit ![]() in
in ![]() ist, während es für mich in
ist, während es für mich in ![]() ist. Da kein
Bezugssystem bevorzugt ist, muss meine Beschreibung der Situation und seine äquivalent
sein. Mein Massstab ist für B verkürzt, während seiner für mich kürzer ist. Der
Verkürzungsfaktor
ist. Da kein
Bezugssystem bevorzugt ist, muss meine Beschreibung der Situation und seine äquivalent
sein. Mein Massstab ist für B verkürzt, während seiner für mich kürzer ist. Der
Verkürzungsfaktor ![]() muss für beide der gleiche sein:
muss für beide der gleiche sein:
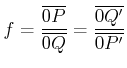 |
(7.387) |
und damit auch
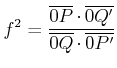
Nun ist
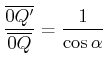
und nach dem Sinussatz
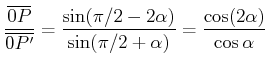
Damit ist
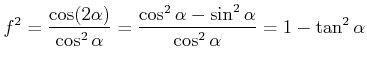 |
(7.388) |
Nun berücksichtigen wir, dass die Steigung bei einer Geschwindigkeit
![]() oder
oder
![]() die Steigung. Wir erhalten
also
die Steigung. Wir erhalten
also
Lorentz-Kontraktion |
In jedem gegen das Inertialsystem des Beobachters mit 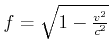 verkürzt. verkürzt. |
Durch die Laufzeiten der Bilder entstehen zusätzliche Verzerrungen, so dass Objekte nicht einfach verkürzt erscheinen.
| Dieser Stoff wurde am 12.12.2001 behandelt |
![\includegraphics[width=0.8\textwidth]{Uhrenvergleich.eps}](img1242.gif)
![\includegraphics[width=0.8\textwidth]{Uhrenvergleich-1.eps}](img1243.gif)
Uhrenvergleich. Oben die traditionelle Darstellung nach (Siehe Gerthsen, Physik[GV95, 842]) , unten die einsichtigere Darstellung.
|
Aus R, beziehungsweise R' kann das Punktereignis ''Uhr zeigt 1'' im anderen Bezugssystem rekonstruiert werden. Die Argumentation wie beim Längenvergleich erfordert9:
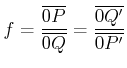
und damit
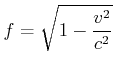 |
(7.390) |
Jeder Beobachter sieht die Uhr des anderen erst später die 1 erreichen. Bewegte Uhren gehen also langsamer wegen der Zeitdilatation.
| Zwischen zwei Punktereignissen misst derjenige Beobachter den kürzesten Zeitabstand, der sie (soweit möglich) direkt erlebt, also für den sie beide ''hier'' sind. |
| Zwischen zwei Punktereignissen misst derjenige den kürzesten Abstand, für den sie gleichzeitig erfolgen (bei ihm ist der Massstab am längsten!). |
Da wir keine Aussage über die Natur der Uhren gemacht haben, müssen wir schliessen, dass die obige Aussage für alle Prozesse gilt.
| Dieser Stoff wurde am 18.12.2001 behandelt |
Materialien
Folien zur Vorlesung am 18. 12. 2001 PDF
Übungsblatt 10 vom 18. 12. 2001 (HTML oder PDF)
![\includegraphics[width=0.8\textwidth]{rel_dopplereffekt.eps}](img1244.gif)
Der relativistische Dopplereffekt. Links ist mein Standpunkt, rechts der von B.
|
Die obige Skizze soll die Frage klären, welche Periode ![]() B misst für ein Signal, das
ich die Periode
B misst für ein Signal, das
ich die Periode ![]() messe.
messe.
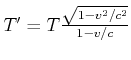
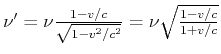
B würde anders argumentieren (rechte Seite der obigen Zeichnung)
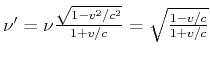
Der Dopplereffekt wird also durch die spezielle Relativitätstheorie konsistent beschrieben.
| Dieser Stoff wurde am 18.12.2001 behandelt |
![\includegraphics[width=0.5\textwidth]{Geschwindigkeitsaddition.eps}](img1257.gif)
Addition von Geschwindigkeiten
|
In diesem Gedankenexperiment sollen B und ich einen Meteoriten beobachten:
Im Punkte ![]() misst B durch Rückdatierung, dass der Meteorit in
misst B durch Rückdatierung, dass der Meteorit in ![]() und er in
und er in ![]() gewesen sind.
gewesen sind.
| Die Länge einer Einheit auf B's |
In dem durch ![]() gegebenen Zeitpunkt bestimmt B die Geschwindigkeit des Meteoriten durch
gegebenen Zeitpunkt bestimmt B die Geschwindigkeit des Meteoriten durch
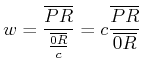 |
(7.391) |
Damit berechnet man
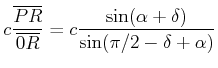 |
|||
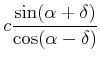 |
|||
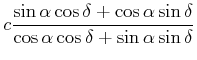 |
|||
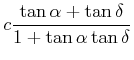 |
|||
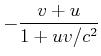 |
(7.392) |
| Die relativistische Summe zweier Geschwindigkeiten ist
ein Wert, der um |
| Dieser Stoff wurde am 18.12.2001 behandelt |
Das folgende Gedankenexperiment soll zur Ableitung des Messverfahrens für relativistische Beschleunigungen dienen.
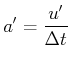
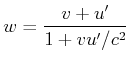
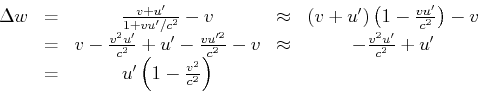
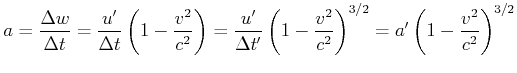
| Die von B gemessene longitudinale Beschleunigung . |
| Dieser Stoff wurde am 18.12.2001 behandelt |
![\includegraphics[width=0.8\textwidth]{relativistische-masse.eps}](img1287.gif)
Gedankenexperiment zur Bestimmung der relativistischen Masse
|
Von dem Startturm aus werden zwei identische Raketen in kurzer Zeit auf die
Geschwindigkeit ![]() oder
oder ![]() gebracht. Im Ruhesystem des Startturms ist klar, dass der
Schwerpunkt
gebracht. Im Ruhesystem des Startturms ist klar, dass der
Schwerpunkt ![]() am Ort bleibt, da wir eine bezüglich des Startturms symmetrische
Situation haben.
am Ort bleibt, da wir eine bezüglich des Startturms symmetrische
Situation haben.
Für den Reisenden in der Rakete ![]() sieht die Situation so aus:
sieht die Situation so aus:
Für den Reisenden in der Rakete ![]() sieht die Situation so aus:
sieht die Situation so aus:
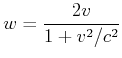
Nach dem 1. Einsteinschen Postulat muss die Beschreibung sowohl für das Ruhesystem des
Startturms wie auch für A (und für B) konsistent sein. Der Schwerpunkt S kann
sich nur dann für ![]() immer über dem Startturm befinden, wenn die Masse von
immer über dem Startturm befinden, wenn die Masse von ![]() ,
, ![]() ,
zunimmt. Der Abstand (für grosse Zeiten) von
,
zunimmt. Der Abstand (für grosse Zeiten) von ![]() zum Startturm im Bezugssystem von
zum Startturm im Bezugssystem von ![]() geht wie
geht wie
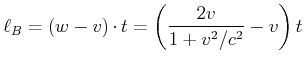 |
(7.396) |
Der Abstand des Startturms von ![]() ist in
ist in ![]() 's Bezugssystem
's Bezugssystem
![]() .
Bezüglich des Schwerpunktes müssen die Drehmomente null sein, also
.
Bezüglich des Schwerpunktes müssen die Drehmomente null sein, also
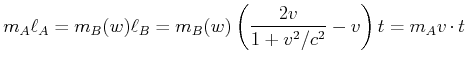 |
(7.397) |
Wir erhalten also
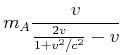 |
|||
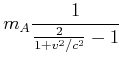 |
|||
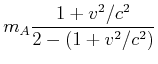 |
|||
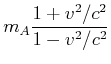 |
|||
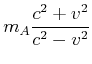 |
(7.398) |
Diese Gleichung sollte nun mit ![]() ausgedrückt werden. Wir verwenden den Trick, dass
ausgedrückt werden. Wir verwenden den Trick, dass
![]() ist10
ist10
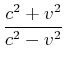 |
|||
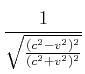 |
|||
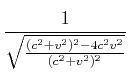 |
|||
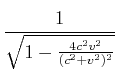 |
|||
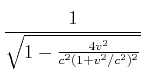 |
(7.399) |
Nun ist aber mit der Gleichung für ![]() auf Seite
auf Seite ![[*]](crossref.gif) gerade
gerade
![]() und damit
und damit
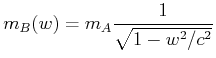 |
(7.400) |
| Die mit der Geschwindigkeit |
Der Rechenweg mit dem Startturm diente dazu, eine Markierung für den Schwerpunkt zu haben. Der Starturm ist eine Hilfskonstruktion.
| Dieser Stoff wurde am 18.12.2001 behandelt |
Nach Gleichung (7.16) wird die Arbeit (Kraft mal Weg), die in eine Masse gesteckt wurde, nicht nur zur Erhöhung der Geschwindigkeit, sondern auch zur Erhöhung der Masse verwendet. Wir können Gleichung (7.16) für kleine Geschwindigkeiten entwickeln
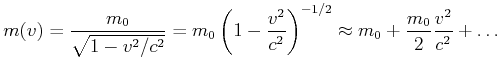 |
(7.402) |
Diese Gleichung könnte man auch als
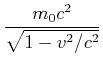 |
|||
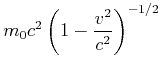 |
|||
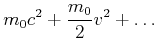 |
|||
| (7.403) |
Nach der relativistischen Mechanik entspricht einer (geschwindigkeitsabhängigen)
Masse die Energie
. |
Die relativistische kinetische Energie ist
| Dieser Stoff wurde am 8. 1. 2002 behandelt |
Materialien
Übungsblatt 11 vom 8. 1. 2002 (HTML oder PDF)
Folien zur Vorlesung am 08. 01. 2002 PDF
Der relativistische Impuls ist analog zum klassischen Impuls definiert:
|
Die relativistische Kraft ist analog zum 2. Newtonschen Axiom durch
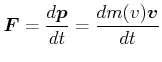 |
(7.407) |
Die Gesamtenergie ![]() kann wie folgt umgeformt werden
kann wie folgt umgeformt werden
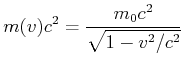 |
|||
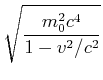 |
|||
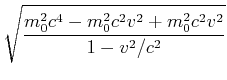 |
|||
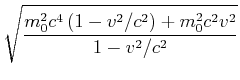 |
|||
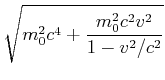 |
|||
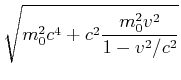 |
|||
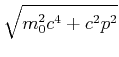 |
(7.408) |
Dieses Resultat nennt man den relativistischen Energiesatz
| Dieser Stoff wurde am 8.1.2002 behandelt |
Wir wollen ausrechnen, wie sich eine Rakete beschleunigt, und verwenden das 2. Newtonsche Axiom
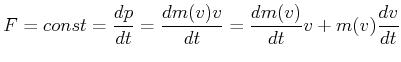 |
(7.410) |
Nun ist
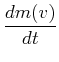 |
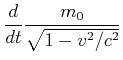 |
||
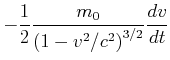 |
(7.411) |
und damit
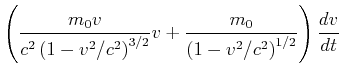 |
|||
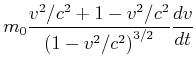 |
|||
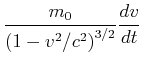 |
(7.412) |
Diese Gleichung kann umgestellt werden. Wir erhalten
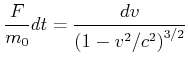 |
(7.413) |
Integration liefert
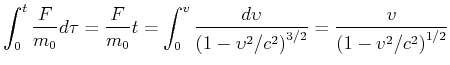 |
(7.414) |
Aufgelöst nach ![]() erhalten wir
erhalten wir
![\includegraphics[width=0.6\textwidth]{rela_vr.eps}](img1342.gif)
Verlauf der Geschwindigkeit bei konstanter Kraft im klassischen (rot) und relativistischen (grün) Fall.
|
Die folgenden Approximationen können gemacht werden:
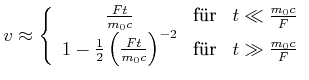 |
(7.416) |
Die Beschleunigung ist im System der Rakete konstant
![]() . Nach
Gleichung (7.9) ist
. Nach
Gleichung (7.9) ist
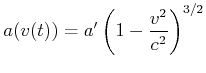 |
(7.417) |
Durch Einsetzen von Gleichung (7.30) (
![]() ) erhalten wir
) erhalten wir
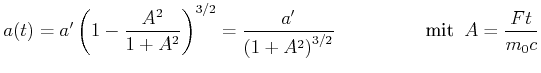 |
(7.418) |
oder
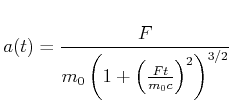 |
(7.419) |
![\includegraphics[width=0.6\textwidth]{rela_ar.eps}](img1349.gif)
Verlauf der Beschleunigung bei konstanter Kraft im klassischen (rot) und relativistischen (grün) Fall.
|
Wir erhalten wieder die Approximationen
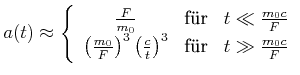 |
(7.420) |
Sowohl bei der Geschwindigkeit wie auch bei der Beschleunigung ist
![]() der klassische Newtonsche Bereich.
der klassische Newtonsche Bereich.
Der Impuls selber nimmt linear mit der Zeit zu, unabhängig, ob eine relativistische oder eine klassische Betrachtung durchgeführt wird. Im klassischen Fall beruht die Impulszunahme auf der Zunahme der Geschwindigkeit, im relativistischen Fall auf der Zunahme der Masse.
Die kinetische Energie ist durch Gleichung (7.20)
gegeben. Setzen wir Gleichung (7.30) (
![]() ), so erhalten wir
), so erhalten wir
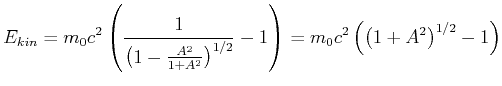 |
(7.421) |
oder
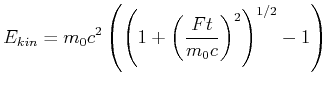 |
(7.422) |
![\includegraphics[width=0.6\textwidth]{rela_ekinr.eps}](img1354.gif)
Verlauf der kinetischen bei konstanter Kraft im klassischen (rot) und relativistischen (grün) Fall.
|
Die Approximation ergibt
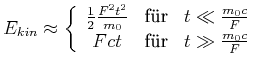 |
(7.423) |
Die kinetische Energie nimmt im relativistischen Falle nur linear mit der Zeit zu.
Mit Gleichung (7.30) kann auch die Distanz als Funktion der Zeit berechnet werden. Wir integrieren
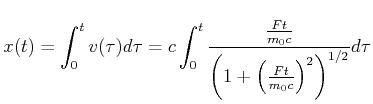 |
(7.424) |
Wir substituieren
![]() und bemerken, dass
und bemerken, dass
![]() ist,
oder auch
ist,
oder auch
![]() .
.
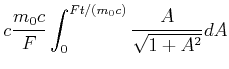 |
|||
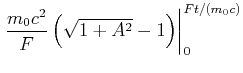 |
|||
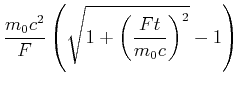 |
(7.425) |
![\includegraphics[width=0.6\textwidth]{rela_xr.eps}](img1363.gif)
Verlauf der zurückgelegten Distanz bei konstanter Kraft im klassischen (rot) und relativistischen (grün) Fall.
|
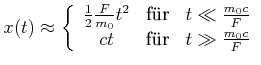 |
(7.426) |
![\includegraphics[width=0.6\textwidth]{rela_tau.eps}](img1365.gif)
Verlauf der Eigenzeit bei konstanter Kraft im klassischen (rot) und relativistischen (grün) Fall.
|
![\includegraphics[width=0.6\textwidth]{rela_x_tau.eps}](img1366.gif)
Zurückgelegte Strecke als Funktion der Eigenzeit.
|