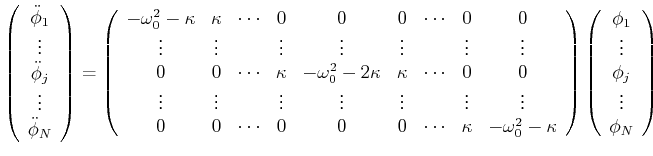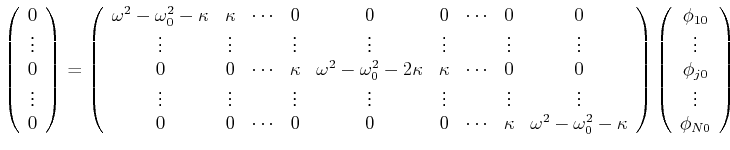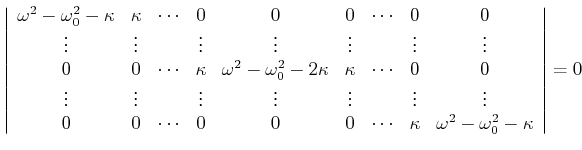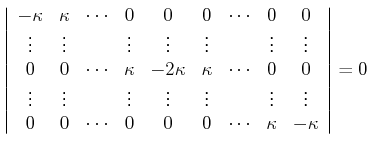




Weiter: Wellen
Oben: Schwingungen
Zurück: Gekoppelte Schwingungen
Skript: PDF-Datei Übungen: Blätter
| Dieser Stoff wurde am 22.1.2002
behandelt |
Wir wollen nun untersuchen, wie die Lösung der Schwingungsgleichung für 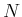 gleich Pendel
aussieht, die jeweils vom
gleich Pendel
aussieht, die jeweils vom 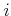 -ten zum
-ten zum 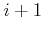 -ten Pendel mit einer masselosen Feder mit der
Federkonstante
-ten Pendel mit einer masselosen Feder mit der
Federkonstante 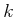 gekoppelt sind. Für das erste Pendel mit
gekoppelt sind. Für das erste Pendel mit 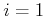 gilt
gilt
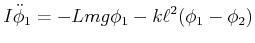 |
(8.536) |
Die Bewegungsgleichung des letzten Pendels ist
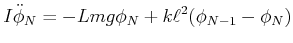 |
(8.537) |
Dazwischen lauten die Bewegungsgleichungen für ein Pendel 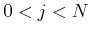
Wir dividieren durch 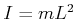 und setzen
und setzen
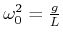 und
und
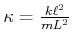 und schreiben die Gleichung als matrizengleichung
und schreiben die Gleichung als matrizengleichung
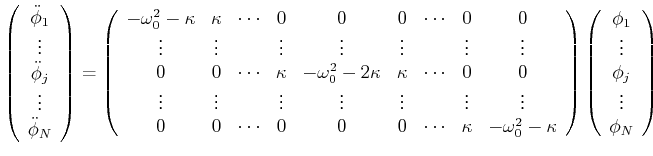 |
(8.539) |
Wir setzen nun
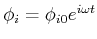 und lösen die obige Gleichung
und lösen die obige Gleichung
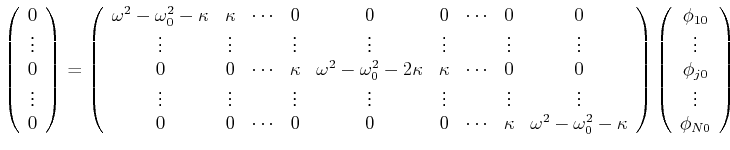 |
(8.540) |
Diese Gleichung hat dann eine Lösung, wenn die Determinante
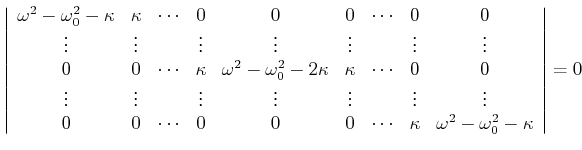 |
(8.541) |
Die Lösung mit der tiefsten Resonanzfrequenz ist
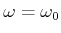 , bei der alle Pendel in Phase sind (bei
allen anderen Bewegungsmoden sit neben der potentiellen Energie der Pendel auch in den Federn
potentielle Energie gespeichert, die Gesamtenergie
also für die gleich Auslenkung grösser.) Wenn wir diese Lösung einsetzen, bekommen wir die Gleichung
, bei der alle Pendel in Phase sind (bei
allen anderen Bewegungsmoden sit neben der potentiellen Energie der Pendel auch in den Federn
potentielle Energie gespeichert, die Gesamtenergie
also für die gleich Auslenkung grösser.) Wenn wir diese Lösung einsetzen, bekommen wir die Gleichung
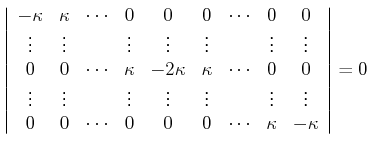 |
(8.542) |
Wenn man alle Zeilen dieser Determinante aufsummiert, bekommt man den Null-Vektor.
Deshalb ist die obige Determinantengleichung erfüllt.





Next: Wellen
Up: Schwingungen
Previous: Gekoppelte Schwingungen
Skript: PDF-Datei Übungen: Blätter
Othmar Marti
Experimentelle Physik
Universiät Ulm
![]() gleich Pendel
aussieht, die jeweils vom
gleich Pendel
aussieht, die jeweils vom ![]() -ten zum
-ten zum ![]() -ten Pendel mit einer masselosen Feder mit der
Federkonstante
-ten Pendel mit einer masselosen Feder mit der
Federkonstante ![]() gekoppelt sind. Für das erste Pendel mit
gekoppelt sind. Für das erste Pendel mit ![]() gilt
gilt