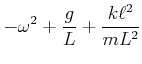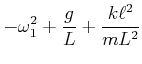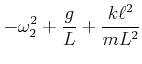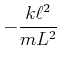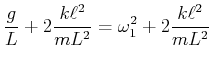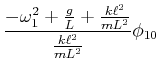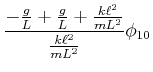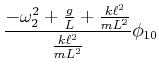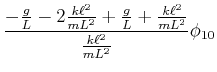




Weiter: Verallgemeinerung: Fundamental- oder Eigenschwingungen
Oben: Schwingungen
Zurück: Überlagerung von Schwingungen
Skript: PDF-Datei Übungen: Blätter
| Dieser Stoff wurde am 22.1.2002
behandelt |
|
Gekoppelte Pendel. Zwei mathematische Pendel im Abstand 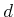 mit jeweils der Länge mit jeweils der Länge 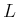 sind mit einer masselosen Feder der Ruhelänge
sind mit einer masselosen Feder der Ruhelänge 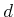 und der Federkonstante und der Federkonstante 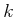 gekoppelt. gekoppelt.
|
Wenn das linke Pendel um 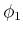 und das rechte Pendel um
und das rechte Pendel um 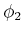 ausgelenkt wird (in
beiden Fällen wird nach rechts positiv gezählt), dann verändert sich die Länge der Feder
um
ausgelenkt wird (in
beiden Fällen wird nach rechts positiv gezählt), dann verändert sich die Länge der Feder
um
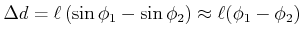 |
(8.517) |
für kleine Auslenkungen. Deshalb ist die Kraft, die auf das linke Pendel ausgeübt wird
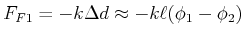 |
(8.518) |
Entsprechend ist die Kraft auf das rechte Pendel
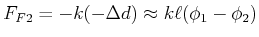 |
(8.519) |
Diese Kräfte entsprechen den Drehmomenten
Die durch die Gravitation hervorgerufenen Momente an den Pendeln sind
Wir beachten, dass für eine Punktmasse 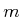 an einem masselosen Faden der Länge
an einem masselosen Faden der Länge 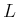 das
Trägheitsmoment
das
Trägheitsmoment 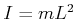 ist und erhalten die linearisierte Momentengleichung
ist und erhalten die linearisierte Momentengleichung
Wir teilen durch 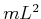 und schreiben in Matrizenform
und schreiben in Matrizenform
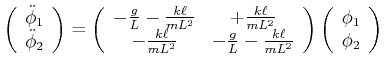 |
(8.523) |
Wir nehmen an, dass beide Pendel mit der gleichen Frequenz 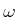 schwingen. Wir setzen
also an
schwingen. Wir setzen
also an
Eingesetzt in Gleichung (8.92) bekommen wir
Wir teilen durch
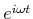
Wir stellen die Gleichung um und sortieren nach den beiden unbekannten
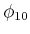 und
und
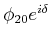 .
.
Wir verwenden die folgenden Abkürzungen
und müssen damit die Gleichung
lösen. Wir multiplizieren die erste Gleichung mit 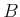 und die zweite mit
und die zweite mit 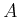 und bekommen
und bekommen
und addieren die Gleichungen. Damit wird
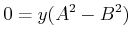 |
(8.531) |
Damit diese Gleichung für alle 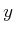 eine Lösung ist, muss
eine Lösung ist, muss 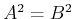 sein. Diese
Bestimmungsgleichung für
sein. Diese
Bestimmungsgleichung für 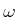 hat zwei Lösungen
hat zwei Lösungen
oder
Wir vereinfachen diese beiden Gleichungen und lösen nach 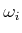 auf
auf
Wenn wir 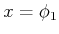 als Vorgabe nehmen und die Gleichung
als Vorgabe nehmen und die Gleichung
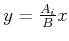 lösen,
bekommen wir die Amplitude des zweiten Pendels.
lösen,
bekommen wir die Amplitude des zweiten Pendels.
Die beiden Lösungen haben die folgenden Charakteristika
- Lösung 1
- Es ist
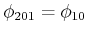 und
und
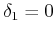 . Die beiden
Pendel schwingen in Phase mit der gleichen Resonanzfrequenz wie ein einzelnes Pendel. Die Feder wird nicht
gedehnt. Ob sie vorhanden ist oder nicht, ist nicht relevant.
. Die beiden
Pendel schwingen in Phase mit der gleichen Resonanzfrequenz wie ein einzelnes Pendel. Die Feder wird nicht
gedehnt. Ob sie vorhanden ist oder nicht, ist nicht relevant.
- Lösung 2
- Es ist
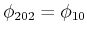 und
und
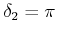 . Die beiden
Pendel schwingen gegenphasig mit einer höheren Resonanzfrequenz als die, die ein einzelnes Pendel hätte.
Die Feder wird periodisch gedehnt und gestaucht.
. Die beiden
Pendel schwingen gegenphasig mit einer höheren Resonanzfrequenz als die, die ein einzelnes Pendel hätte.
Die Feder wird periodisch gedehnt und gestaucht.





Next: Verallgemeinerung: Fundamental- oder Eigenschwingungen
Up: Schwingungen
Previous: Überlagerung von Schwingungen
Skript: PDF-Datei Übungen: Blätter
Othmar Marti
Experimentelle Physik
Universiät Ulm
![\includegraphics[width=0.8\textwidth]{schwingung-gekoppelte-Pendel.eps}](img1618.gif)
![]() mit jeweils der Länge
mit jeweils der Länge ![]() sind mit einer masselosen Feder der Ruhelänge
sind mit einer masselosen Feder der Ruhelänge ![]() und der Federkonstante
und der Federkonstante ![]() gekoppelt.
gekoppelt.
![\includegraphics[width=0.8\textwidth]{schwingung-gekoppelte-Pendel.eps}](img1618.gif)
![]() und das rechte Pendel um
und das rechte Pendel um ![]() ausgelenkt wird (in
beiden Fällen wird nach rechts positiv gezählt), dann verändert sich die Länge der Feder
um
ausgelenkt wird (in
beiden Fällen wird nach rechts positiv gezählt), dann verändert sich die Länge der Feder
um
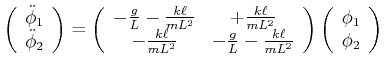
![]() schwingen. Wir setzen
also an
schwingen. Wir setzen
also an
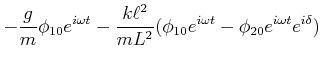
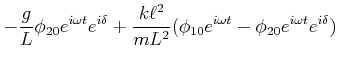
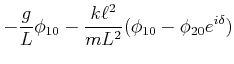
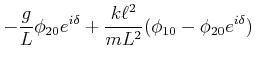
![$\displaystyle \left[-\omega^2+\frac{g}{L}+\frac{k\ell^2}{mL^2}\right]\phi_{1,0}-\frac{k\ell^2}{mL^2}\phi_{2,0}e^{i\delta}$](img1654.gif)
![$\displaystyle - \frac{k\ell^2}{mL^2}\phi_{1,0}+\left[-\omega^2 +\frac{g}{L} +\frac{k\ell^2}{mL^2}\right]\phi_{2,0}e^{i\delta}$](img1655.gif)