| (9.567) |
| Dieser Stoff wurde am 29.1.2002 behandelt |
Die Wellenfunktion für eine Welle in zwei oder drei Dimensionen wird wie
| (9.567) |
| (9.569) |
| Dieser Stoff wurde am 29.1.2002 behandelt |
![\includegraphics[width=0.4\textwidth]{wellen-eben.eps}](img1783.gif)
Bild einer ebenen Welle
|
Eine ebene Welle entsteht aus der allgemeinen Wellengleichung dadurch, dass die Amplitude und der Wellenvektor nicht vom Ort abhängen. Eine ebene Transversalwelle ist durch
| (9.570) |
| (9.571) |
| Dieser Stoff wurde am 29.1.2002 behandelt |
Eine weitere häufig vorkommende Form von Wellen sind die Kugelwellen. Wir können die Amplitudenabhängigkeit durch folgende Überlegung erhalten.
![\includegraphics[width=0.45\textwidth]{welle_kugel_amplitude.eps}](img1793.gif)
![\includegraphics[width=0.45\textwidth]{welle_kugel_amplitude_log.eps}](img1794.gif)
Amplitude und Intensität einer Kugelwelle in Abhängigkeit der Distanz
|
Bei einer Kugelwelle ist
|
Bei einer Wasserwelle auf der Wasseroberfläche ist die durch eine Kreis mit dem Umfang
![]() gehende Leistung konstant. Deshalb gilt, dass bei Wellen, die sich auf einer
2-dimensionalen Oberfläche bewegen, dass
gehende Leistung konstant. Deshalb gilt, dass bei Wellen, die sich auf einer
2-dimensionalen Oberfläche bewegen, dass
|
ist.
Allgemein ist bei einem ![]() -dimensionalen Raum
-dimensionalen Raum
| Dieser Stoff wurde am 29.1.2002 behandelt |
Bei Wasserwellen können Interferenzerscheinungen sehr schön beobachtet werden. Die folgenden Abbildungen zeigen schematisch die zu beobachtenden Interferenzmuster.
![\includegraphics[width=0.6\textwidth]{wellen-eben-interferenz.eps}](img1801.gif)
Interferenz zweier ebener Wellen. Blau sind die Wellenberge zu einer bestimmten Zeit markiert. Die roten Pfeile
geben die
|
![\includegraphics[width=0.4\textwidth]{wellen-eben-inter-30-30.eps}](img1803.gif)
![\includegraphics[width=0.4\textwidth]{wellen-eben-inter-15-15.eps}](img1804.gif)
Interferenz ebener Wellen. Die Kantenlänge der Bilder ist 20. Der Betrag des Wellenvektors ist
|
![\includegraphics[width=0.4\textwidth]{wellen-eben-inter-5-5.eps}](img1808.gif)
![\includegraphics[width=0.4\textwidth]{wellen-eben-kugel-inter-6-3.eps}](img1809.gif)
Links Interferenz ebener Wellen, rechts die Interferenz einer Kreiswelle mit einer ebenen Welle. Die Kantenlänge
der Bilder ist 20. Der Betrag des Wellenvektors ist
|
Die Maxima und Minima sind durch eine konstante Differenz der Phase und damit des Abstandes von zwei Referenzlinien, die parallel zu den jeweiligen Fronten liegen , charakterisiert. Damit sind auch die Orte konstanter Phase Geraden.
![\includegraphics[width=0.4\textwidth]{wellen-eben-kugel-inter-6-5.eps}](img1811.gif)
![\includegraphics[width=0.4\textwidth]{wellen-eben-kugel-inter-6-8.eps}](img1812.gif)
Interferenz einer Kreiswelle mit einer ebenen Welle. Die Kantenlänge der Bilder ist 20. Das Zentrum der Kugelwelle
von der Mitte aus um 6 nach oben versetzt. Links ist der Betrag des Wellenvektors
|
Die Lage der Maxima oder der Minima ist durch eine konstante Phasendifferenz
kennzeichnet. Wenn die ebene Welle sich in y-Richtung Ausbreitet, dann nimmt man eine zur
x-Achse parallele Linie durch die Quelle der Kreiswelle als Referenz. Wenn ![]() der
Abstand des Punktes
der
Abstand des Punktes ![]() von dieser Linie sei und
von dieser Linie sei und ![]() der Abstand von
der Abstand von ![]() von der
punktförmigen Quelle, dann gilt für den Abstand
von der
punktförmigen Quelle, dann gilt für den Abstand ![]() von
von ![]() parallel zur x-Achse,
dass
parallel zur x-Achse,
dass
| (9.572) |
| (9.573) |
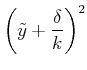 |
|||
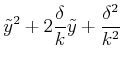 |
|||
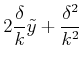 |
|||
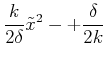 |
(9.574) |
![\includegraphics[width=0.4\textwidth]{wellen-kugel-inter-1-1.eps}](img1826.gif)
![\includegraphics[width=0.4\textwidth]{wellen-kugel-inter-2-2.eps}](img1827.gif)
Interferenz zweier Kugelwellen mit dem Wellenvektor vom Betrag
|
Die Orte konstanter Phasen, also die Lage der Maxima und Minima ist durch eine konstante
Wegdifferenz von einem Punkt ![]() zu den Quellen charakterisiert. Wir legen die Quellen an
die Punkte
zu den Quellen charakterisiert. Wir legen die Quellen an
die Punkte
![]() und
und
![]() . Die Abstände des Punktes
. Die Abstände des Punktes ![]() seien
seien
![]() und
und
![]() . Es ist dann
. Es ist dann
![]() .
Eingesetzt
.
Eingesetzt
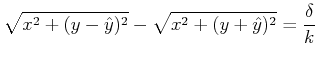 |
![\includegraphics[width=0.4\textwidth]{wellen-kugel-inter-4-4.eps}](img1835.gif)
![\includegraphics[width=0.4\textwidth]{wellen-kugel-inter-8-8.eps}](img1836.gif)
Interferenz zweier Kugelwellen mit dem Wellenvektor vom Betrag
|
| Dieser Stoff wurde am 29.1.2002 behandelt |
Die Beugung von Wasserwellen an einem Objekt kann mit dem Prinzip von Huygenserklärt werden. Man nimmt eine Momentaufnahme des Wellenbildes eines bestimmten Wellenberges und nimmt jeden Punkt auf diesem Wellenberg als Ausgangspunkt einer neuen Kreiswelle (Kugelwelle in 3 Dimensionen).
![\includegraphics[width=0.4\textwidth]{huygens-2.eps}](img1837.gif)
![\includegraphics[width=0.4\textwidth]{huygens-4.eps}](img1838.gif)
Huygens'sches Prinzip. Links die Interferenz von 5 Kreiswellen auf einer horizontalen Linie, die 4 mal so lang ist wie die Bildkante. Rechts das gleiche mit 9 Kreiswellen.
|
![\includegraphics[width=0.4\textwidth]{huygens-8.eps}](img1839.gif)
![\includegraphics[width=0.4\textwidth]{huygens-16.eps}](img1840.gif)
Huygens'sches Prinzip. Links die Interferenz von 17 Kreiswellen auf einer horizontalen Linie, die 4 mal so lang ist wie die Bildkante. Rechts das gleiche mit 33 Kreiswellen.
|
![\includegraphics[width=0.4\textwidth]{huygens-32.eps}](img1841.gif)
![\includegraphics[width=0.4\textwidth]{huygens-64.eps}](img1842.gif)
Huygens'sches Prinzip. Links die Interferenz von 65 Kreiswellen auf einer horizontalen Linie, die 4 mal so lang ist wie die Bildkante. Rechts das gleiche mit 129 Kreiswellen.
|
Die Beugung an einem Spalt kann nun so verstanden werden, dass nicht mehr Kreiswellen aus einem grossen Bereich, sondern nur noch Kreiswellen aus dem Spalt zum neuen Wellenbild beitragen.
![\includegraphics[width=0.4\textwidth]{huygens-slit-2.eps}](img1843.gif)
![\includegraphics[width=0.4\textwidth]{huygens-slit-4.eps}](img1844.gif)
Huygens'sches Prinzip. Interferenzmuster an einem Spalt. Links die Interferenz von 5 Kreiswellen auf einer horizontalen Linie im Spalt. Rechts das gleiche mit 9 Kreiswellen.
|
![\includegraphics[width=0.4\textwidth]{huygens-slit-width-1.eps}](img1845.gif)
![\includegraphics[width=0.4\textwidth]{huygens-slit-width-3.eps}](img1846.gif)
Huygens'sches Prinzip. Interferenzmuster an einem Spalt. Links das Interferenzmuster bei einer Spaltbreite von 1 Wellenlänge, rechts von 3 Wellenlängen.
|
![\includegraphics[width=0.8\textwidth]{huygens-grating.eps}](img1847.gif)
Huygens'sches Prinzip. Interferenzmuster an einem Gitter. Die im Bild sichtbare Drehung rührt daher, dass nur eine endliche Anzahl von Gitterschlitzen berücksichtigt wurde.
|
| Bei Transversalwellen tritt Interferenz nur zwischen den Wellen auf, die eine gemeinsame Schwingungsrichtung des Feldvektors haben! |
Zwei in die x-Richtung laufende Wellen mit den Amplituden
![]() und
und
![]() interferieren nicht. Es bilden sich keine stehenden Wellen, die Orientierung des Summen-Feldvektors
hängt aber von der Position ab.
interferieren nicht. Es bilden sich keine stehenden Wellen, die Orientierung des Summen-Feldvektors
hängt aber von der Position ab.