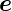 x =
x = 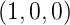 T um den Winkel α wird durch die
Matrix
T um den Winkel α wird durch die
Matrix

Eine Drehung um die x-Achse beschrieben durch den
Vektor 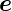 x =
x = 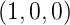 T um den Winkel α wird durch die
Matrix
T um den Winkel α wird durch die
Matrix
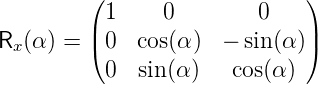 | (D.1) |
die Transformation ausgeführt. Für eine Drehung um die
y-Achse beschrieben durch den Vektor 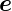 y =
y = 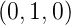 T um den
Winkel β wird durch die Matrix
T um den
Winkel β wird durch die Matrix
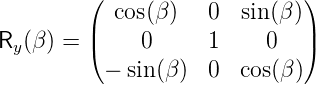 | (D.2) |
die Transformation ausgeführt. Schliesslich wird eine Drehung
um die y-Achse beschrieben durch den Vektor 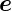 z =
z = 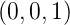 T
um den Winkel γ wird durch die Matrix
T
um den Winkel γ wird durch die Matrix
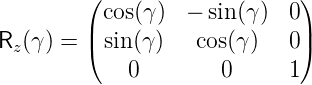 | (D.3) |
ausgeführt.
Der Vektor 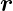 =
= 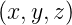 T soll um den Winkel α um die
x-Achse gedreht werden. Dies wird mit der Operation
T soll um den Winkel α um die
x-Achse gedreht werden. Dies wird mit der Operation
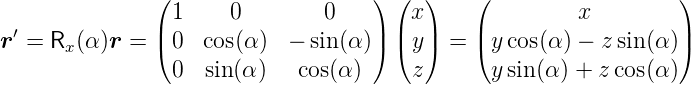 | (D.4) |
bewerkstelligt. Im Allgemeinen wird eine Drehung durch die Multiplikation des Vektors von links mit einer Matrix beschrieben.
Die Drehung zurück wird (antisymmetrische reelle Matrix mit der Determinante 1) wird durch die inverse Matrix oder die transponierte Matrix beschrieben Alternativ kann man auch α durch −α ersetzen.
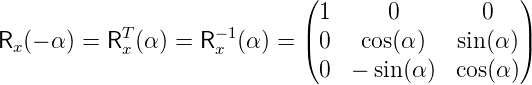 | (D.5) |
Eine Drehung um einen beliebigen Vektor  α =
α = 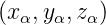 T
mit xα2 + y
α2 + z
α2 = 1 wird durch
T
mit xα2 + y
α2 + z
α2 = 1 wird durch
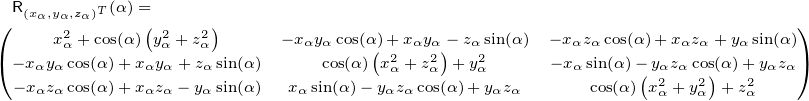 | (D.6) |
beschrieben[WR14]. Die Drehung ist bei positivem α
rechtshändig bezüglich der Richtung von 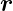 α (Der Daumen
zeigt in die Richtung von
α (Der Daumen
zeigt in die Richtung von 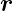 α, die Finger geben die
Drehrichtung).
α, die Finger geben die
Drehrichtung).
Sei R α(α) die Drehmatrix. Dann ist der aus
α(α) die Drehmatrix. Dann ist der aus 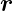 hervorgegangene
um die Achse
hervorgegangene
um die Achse 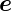 α und den Winkel α gedrehte Vektor
α und den Winkel α gedrehte Vektor
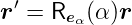 | (D.7) |
Ein Beispiel dafür ist in (D.4) gezeigt.
Die aus der Matrix
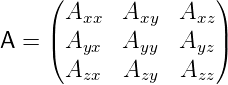
hervorgegangene um die Achse 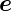 α und den Winkel α
gedrehte Matrix ist
α und den Winkel α
gedrehte Matrix ist
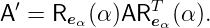 | (D.8) |
Die Drehung zurück ist dann
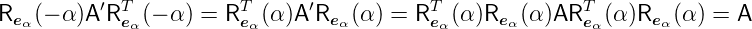 | (D.9) |
Wenn wir als Beispiel die Matrix
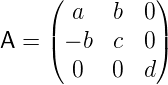
um 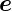 α =
α = 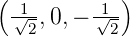 T drehen, erhalten wir
T drehen, erhalten wir
Das Koordinatensystem 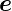 x,
x,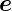 y,
y,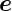 z geht durch drei Drehungen
aus dem Koordinatensystem
z geht durch drei Drehungen
aus dem Koordinatensystem 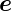 x∗,
x∗,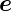 y∗,
y∗,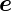 z∗ hervor.
z∗ hervor.
__________________________________________________________________________
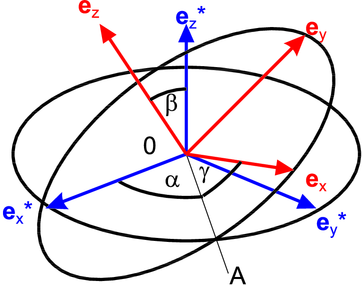
Definition der Eulerschen Winkel
_____________________________________________________________________
Die Eulerschen Winkel sind
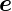 z∗ : α
z∗ : α
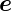 z∗ : γ
z∗ : γ Dabei 0A steht senkrecht zur Ebene aufgespannt durch 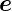 z
und
z
und 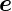 z∗.
z∗.
Die Reihenfolge der Drehungen ist
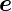 x∗ senkrecht zu
x∗ senkrecht zu 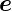 z (In der
Abbildung D.5.3 zeigen die Kreise die Ebenen
senkrecht zu
z (In der
Abbildung D.5.3 zeigen die Kreise die Ebenen
senkrecht zu 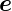 z∗ und senkrecht zu
z∗ und senkrecht zu 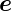 z Die Schnittlinie
der beiden Kreise ist 0A.
z Die Schnittlinie
der beiden Kreise ist 0A.
 Lizenzinformationen
Lizenzinformationen