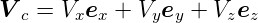
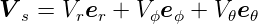
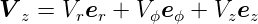
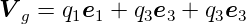

(Siehe Bronstein, Taschenbuch der Mathematik [BSMM08, pp. 218])
(Siehe Bronstein, Taschenbuch der Mathematik [BSMM08, pp. 667])
(Siehe Arfken und Weber, Mathematical Methods for Physicists, [AW95, pp. 100])
Wir betrachten lokal orthogonale Systeme:
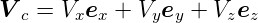
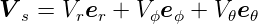
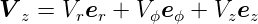
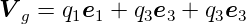
Bei allen Koordinatensystemen sei für alle i 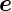 12 = 1. Die
12 = 1. Die
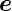 i sollen ein rechtshändiges System bilden, also dass
i sollen ein rechtshändiges System bilden, also dass
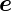 1·
1·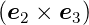 > 0 (wobei die Zahlen 1 bis 3 die drei
Koordinaten in den jeweiligen Systemen in der oben
angegebenen Reihenfolge sind.
> 0 (wobei die Zahlen 1 bis 3 die drei
Koordinaten in den jeweiligen Systemen in der oben
angegebenen Reihenfolge sind.
__________________________________________________________________________
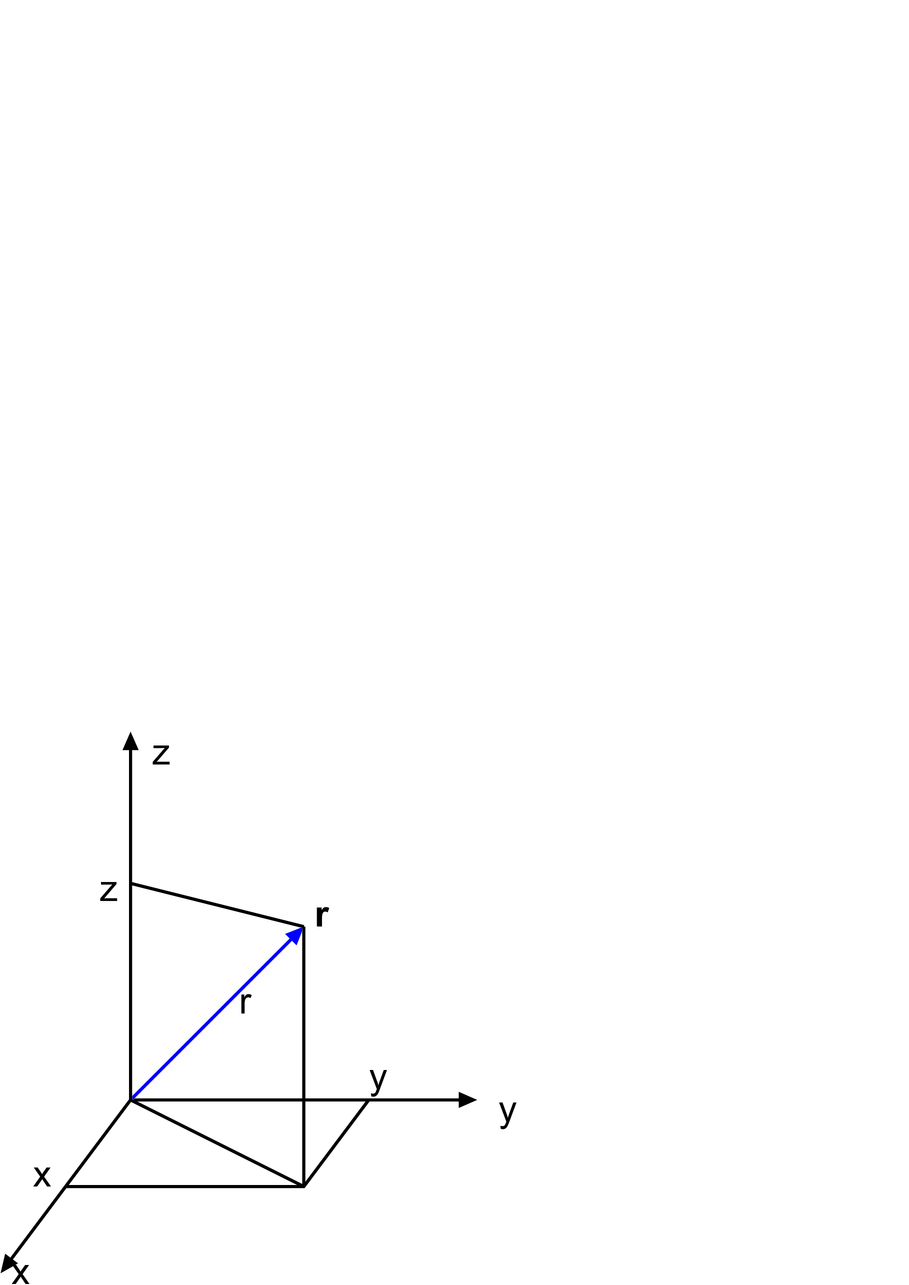
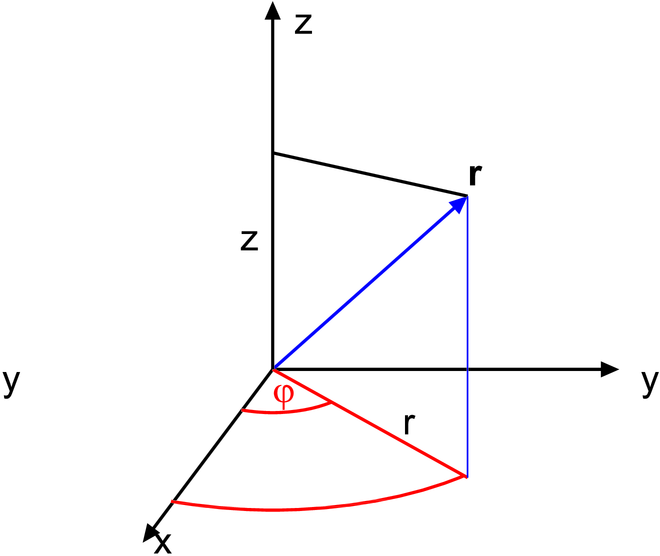
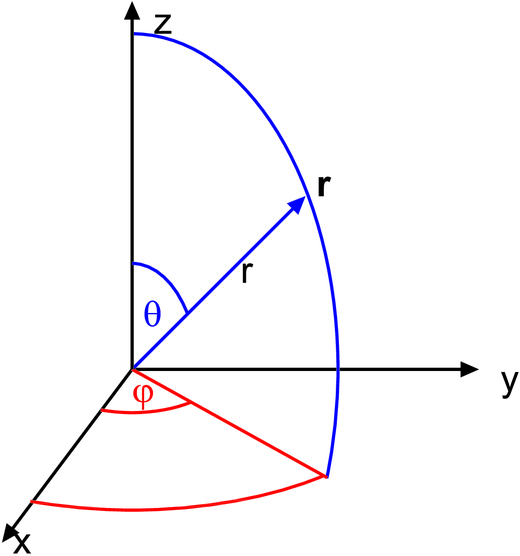
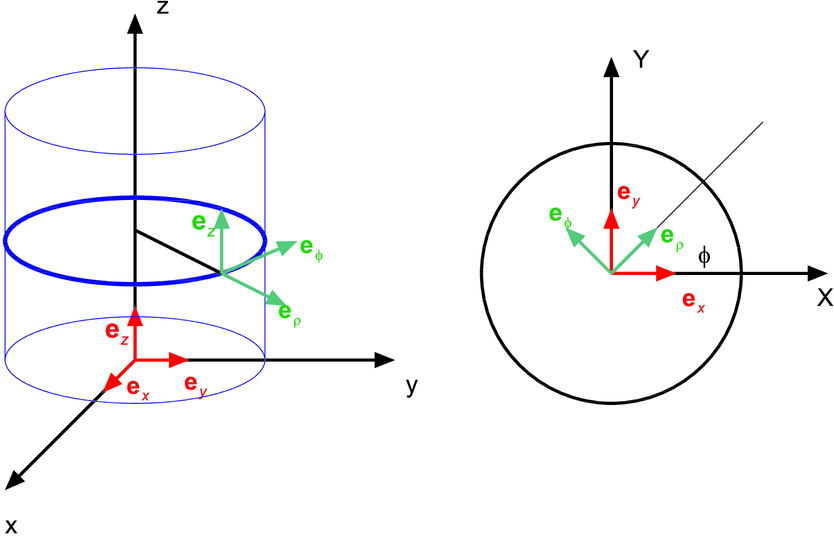
Definition der Koordinatensysteme. Links: kartesisches System. Mitte: Zylinderkoordinaten. Rechts: Kugelkoordinaten
_____________________________________________________________________
Dieser Abschnitt folgt [AW95, p. 100]. Wenn die Transformation von einem beliebigen gekrümmten Koordinatensystem mit den Koordinaten (q1,q2,q3)T in das kartesische System (x,y,z)T bekannt ist, können über das kartesische System als Zwischensystem beliebige gekrümmte, lokal orthogonale Koordinatensystem differenziell ineinander übergeführt werden.
Sei nach
Infinitesimale Verschiebungen führen nach [AW95, p. 100] (D.1) zu
Ausgehend vom infinitesimalen Abstand bei kartesischen Koordinaten ds2 = dx2 + dy2 + dz2 postuliert man
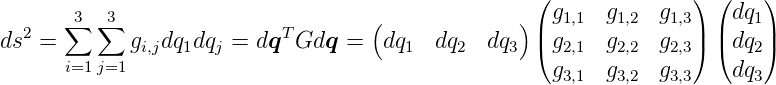 | (D.6) |
Andererseits erhält man aus den quadrierten Gleichungen (D.3) bis (D.5)
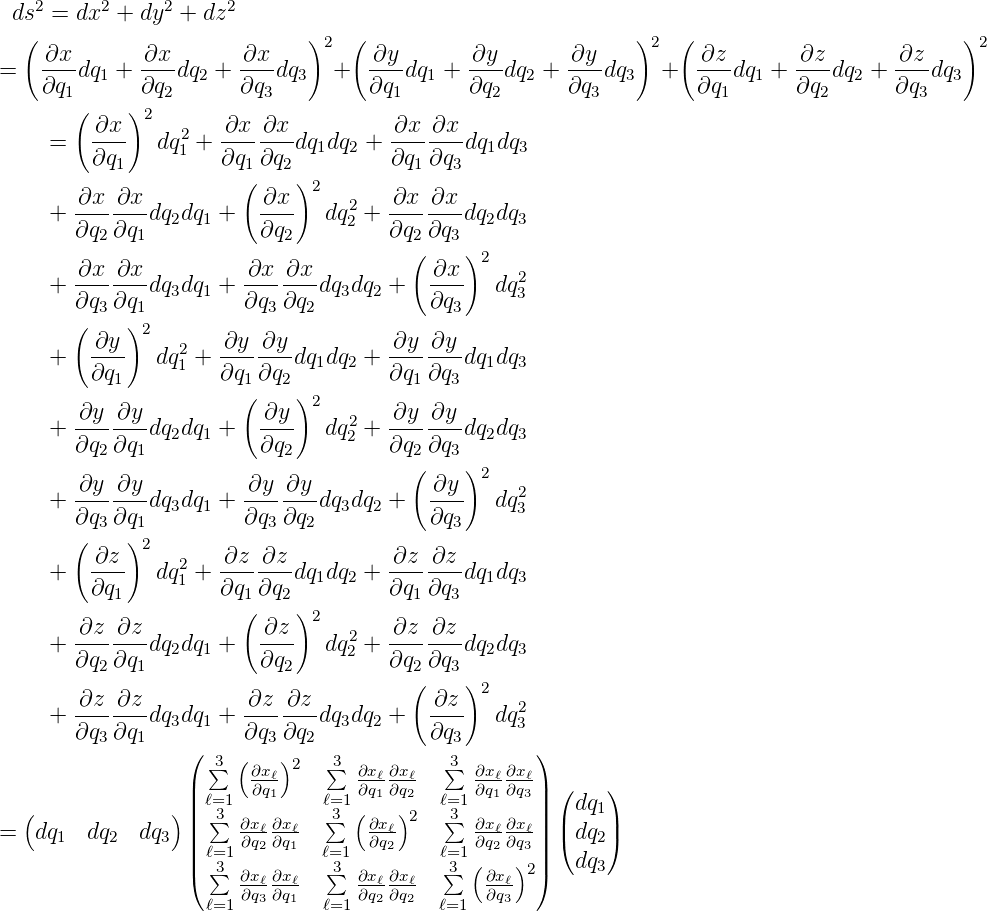 | (D.7) |
wobei x1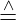 x, x2
x, x2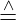 y und x3
y und x3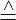 z. Die Matrix
z. Die Matrix
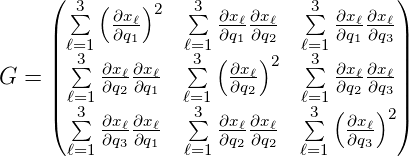 | (D.8) |
heisst Metrik. Beil lokal orthogonalen Koordinatensystemen ist
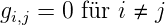 | (D.9) |
und
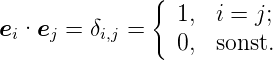 | (D.10) |
Mit der Definition
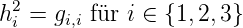 | (D.11) |
erhalten wir
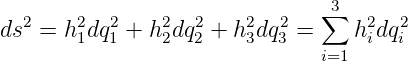 | (D.12) |
Die hi sind Skalenfaktoren, die die gekrümmten Koordinaten dqi in Wegelemente dsi umrechnen:
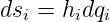 | (D.13) |
Weiter haben wir für eine infinitesimale vektorielle Verschiebung
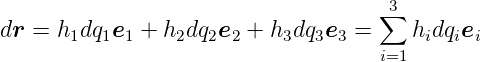 | (D.14) |
Weitere Beziehungen sind
Bemerkung: Skalar- und Vektorprodukt haben in diesen gekrümmten Koordinaten die gleiche Form wie im kartesischen Koordinatensystem.
Wir betrachten das Koordinatensystem
das in der Elektrostatik und Hydrodynamik angewandt wird. Wir sollten gemäss unserem Rezept x, y und z mit u, v und z ausdrücken. Es gibt vier Möglichkeiten, wir verwenden als Beispiel die erste.
Die Skalenfaktoren sind dann mit (D.11), also hi = ∑
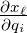
Die Transformation zwischen den Koordinatensystemen läuft auf eine allgemeine Drehung der Koordinaten im Raum hinaus.
__________________________________________________________________________
Umrechnung der Koordinaten
_____________________________________________________________________
 Lizenzinformationen
Lizenzinformationen