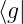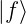 = f und
= f und 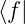 = (f∗)T =
f† wird H × H → ℂ : (f∗,g) =
= (f∗)T =
f† wird H × H → ℂ : (f∗,g) = 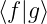 =
∫
−∞+∞f∗(u)g(u)du.
=
∫
−∞+∞f∗(u)g(u)du.Zu Beginn folgen einige mathematische Definitionen, die für die korrekte Formulierung der Gesetze und Regeln notwendig sind. Der mathematische Formalismus beruht auf Hilbert-Räumen (siehe [Sch13, p. 84] und [AW95, p. 585ff und p. 545ff]. Ein Hilbert-Raum wird wie folgt definiert:
H ist ein linearer Vektorraum über dem Raum der komplexen Zahlen ℂ mit den Eigenschaften:
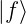 = f und
= f und 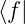 = (f∗)T =
f† wird H × H → ℂ : (f∗,g) =
= (f∗)T =
f† wird H × H → ℂ : (f∗,g) = 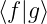 =
∫
−∞+∞f∗(u)g(u)du.
=
∫
−∞+∞f∗(u)g(u)du. Die Norm einer beliebigen Funktion f ∈H ist definiert als
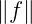 = (
= (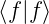 )1∕2
)1∕2
Weil H ein linearer Vektorraum ist, gelten die folgenden Eigenschaften:
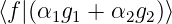 = α1
= α1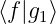 + α2
+ α2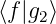
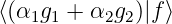 = α∗
1
= α∗
1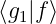 + α∗
2
+ α∗
2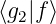
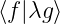 =
= 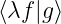 = λ
= λ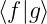 , mit λ ∈ ℂ konstant
, mit λ ∈ ℂ konstant
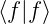 ≥ 0
≥ 0
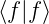 = 0 ⇒ f = 0
= 0 ⇒ f = 0
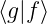 =
= 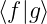 ∗
∗ Ein Vektorraum ist vollständig, wenn es für jedes f eine
Reihe f1,f2,f3,…fn → f gibt, so dass lim n→∞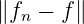 = 0
gilt.
= 0
gilt.
Wenn für das Skalarprodukt von f ∈ H und g ∈ H
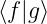 = 0 gilt, dann sind f und g orthogonal.
= 0 gilt, dann sind f und g orthogonal.
Wenn für einen linearen Operator 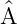 und eine Funktion f ∈H
die Gleichung
und eine Funktion f ∈H
die Gleichung 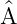 f = af gilt, dann ist f eine Eigenfunktion
von
f = af gilt, dann ist f eine Eigenfunktion
von 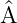 . a ist der entsprechende Eigenwert von
. a ist der entsprechende Eigenwert von 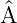 .
.
Hermitesche Operatoren sind Operatoren, für die die folgende Gleichung gilt
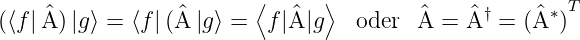 | (5.1) |
Für zahlenwertige (eindimensionale) Operatoren und
Objekte ist f† = f∗. Zum Beispiel sind die Operatoren
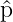 x = (ℏ∕i)(∂∕∂x) und
x = (ℏ∕i)(∂∕∂x) und 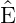 = i(∂∕∂t) hermitesch.
= i(∂∕∂t) hermitesch.
Die Eigenfunktionen eines hermiteschen Operators sind orthogonal und die dazugehörigen Eigenwerte sind reell.
Für hermitesche Operatoren gelten die Rechenregeln [Sch13, p. 24f]:
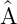
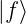 =
= 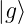 ist äquivalent zu
ist äquivalent zu 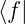
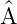 †
=
†
= 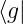
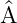
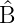 )
)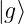 =
= 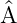 (
(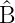
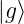 )
und
)
und 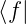 (
(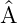
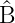 ) = (
) = (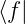
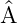 )
)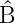
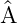 †
)†
=
†
)†
= 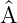
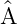 )†
= λ∗
)†
= λ∗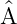 † für λ ∈ℂ
† für λ ∈ℂ 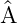 +
+ 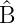 )†
=
)†
= 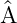 †
+
†
+ 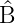 †
†
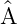
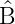 )†
=
)†
= 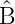 †
†
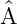 †
†
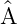 (
(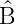
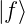 ) =
) = 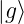 ist äquivalent zu (
ist äquivalent zu (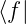
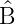 †
)
†
)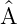 †
=
†
=