Weiter: Zusammenfassung: Ströme Oben: Elektrische Ströme Zurück: Hall-Effekt Skript: PDF-Datei Übungen: Blätter
(Siehe Leisi, Klassische Physik II [Lei98, pp. 128])
Wir betrachten die Situation im Bild zum Halleffekt, nun aber vom Ruhesystem der Platte aus. Hier haben die Elektronen keine Geschwindigkeit: es gibt keine Lorentzkraft.
![\includegraphics[width=0.7\textwidth]{strom-015}](img1069.gif)
Bewegte Magnetfelder und elektrische Felder.
|
Die obige Abbildung zeigt homogene Magnetfelder und elektrische Felder. Sie werden erzeugt, indem zwei parallele
Platten positiv beziehungsweise negativ geladen sind. Wenn die Platten mit der Geschwindigkeit ![]() bewegt
werden ergibt sich auch ein Magnetfeld.
bewegt
werden ergibt sich auch ein Magnetfeld.
Das elektrische Feld beider Platten im Bezugssystem ![]() ist
ist
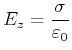 |
(3.308) |
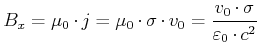 |
(3.309) |
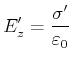 |
(3.310) |
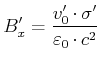 |
(3.311) |
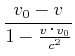 |
(3.312) | ||
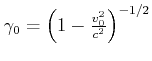 ist. Wir bekommen
ist. Wir bekommen
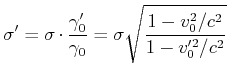 |
(3.313) |
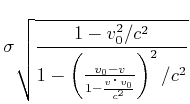 |
(3.314) | ||
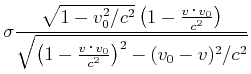 |
|||
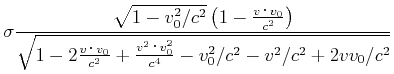 |
|||
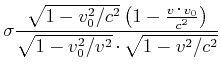 |
|||
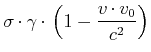 |
 |
|||
 |
|||
| (3.315) |
Damit ist
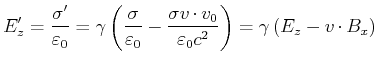 |
(3.316) |
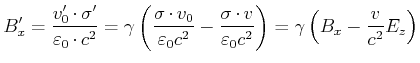 |
(3.317) |
Die Transformationseigenschaften von ![]() und
und ![]() erhält man, indem man die obige Anordnung um
erhält man, indem man die obige Anordnung um ![]() um die
um die
![]() -Achse dreht. Dann gehen
-Achse dreht. Dann gehen
| (3.318) | |||
| (3.319) | |||
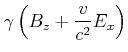 |
![\includegraphics[width=0.7\textwidth]{strom-016}](img1113.gif)
Lorentztransformation von
|
Die Transformation des longitudinalen ![]() -Feldes ergibt sich aus der Erkenntnis, dass transversal zur
Geschwindigkeit keine Längenkontraktion auftritt und dass das Elektrische Feld eines
Plattenkondensators12 nicht
vom Plattenabstand abhängt. Also ist
-Feldes ergibt sich aus der Erkenntnis, dass transversal zur
Geschwindigkeit keine Längenkontraktion auftritt und dass das Elektrische Feld eines
Plattenkondensators12 nicht
vom Plattenabstand abhängt. Also ist
| (3.320) | |||
| (3.321) |
Die Transformationseigenschaften des Magnetfeldes können mit der in der obigen Abbildung rechts angedeuteten Spule berechnet werden. Das Magnetfeld in der Spule ist
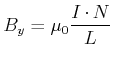 |
(3.322) |
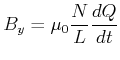 |
(3.323) |
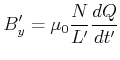 |
(3.324) |
| (3.325) |
Bei einer Bewegung in die 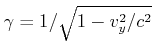 )
werden die elektrischen und magnetische Induktion wie )
werden die elektrischen und magnetische Induktion wie
transformiert. |
Im Vakuum gilt
![]() . Die Lorentztransformation
für elektrische und magnetische Felder ist dann
. Die Lorentztransformation
für elektrische und magnetische Felder ist dann
Othmar Marti