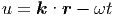

Es gibt eine grosse Klasse von Funktionen (skalar oder vektoriell), die die Wellenleitergleichung lösen. Im Folgenden besprechen wir skalare Funktionen, die aber auch als eine Vektorkomponente aufgefasst werden können. Alle Funktionen, die nur von einer skalaren Variablen
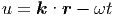 | (6.1) |
abhängen lösen die Wellengleichung, wenn sie genügend oft stetig differenzierbar
sind. Wir betrachten die Funktion f(u) = f(u(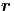 ,t)). und setzen sie in
c2Δf(u(
,t)). und setzen sie in
c2Δf(u(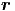 ,t)) = (∂2∕∂t2)f(u(
,t)) = (∂2∕∂t2)f(u(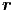 ,t)) ein. Die Kettenregel der Differentiation ergibt für
u =
,t)) ein. Die Kettenregel der Differentiation ergibt für
u = 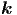 ·
·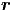 - ωt = kxx + kyy + kzz - ωt
- ωt = kxx + kyy + kzz - ωt
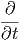 f(u(x,y,z,t)) f(u(x,y,z,t)) | = 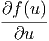 · ·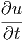 | (6.2) | |
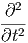 f(u(x,y,z,t)) f(u(x,y,z,t)) | = 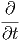 · ·![[ ]
∂f(u(x,-y,z,t))· ∂u-
∂u ∂t](el-20131458x.png) | ||
= 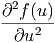 · ·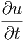 · ·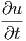 + + 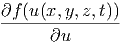 · ·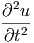 | |||
= 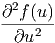 · ·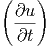 2 2 | (6.3) |
Die letzte Umformung in Gleichung (6.3) beruht auf
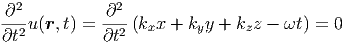 |
Da (∂∕∂t)u = -ω ist, ist auch
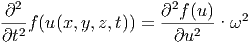 | (6.4) |
Analog erhalten wir für die Raumkomponente x
 f(u(x,y,z,t)) f(u(x,y,z,t)) | = 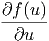 · ·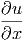 | (6.5) | |
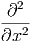 f(u(x,y,z,t)) f(u(x,y,z,t)) | = 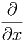 · ·![[ ]
∂f (u(x,y,z,t)) ∂u
---------------· ---
∂u ∂x](el-20131473x.png) | ||
= 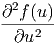 · ·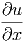 · ·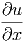 + + 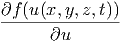 · ·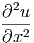 | |||
= 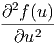 · ·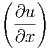 2 2 | (6.6) |
Also ist
Δf(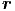 ,t) ,t) | = Δf(u(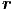 ,t)) ,t)) | ||
= 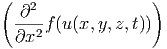 + + 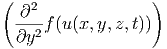 + + 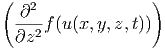 | |||
= 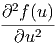 · ·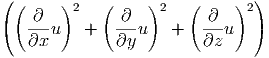 | |||
= 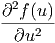 · ·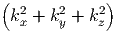 | |||
= 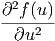 · ·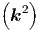 | (6.7) |
Damit lautet die Wellengleichung mit Gleichung (6.3) , Gleichung (6.6) , Gleichung (6.4) und Gleichung (6.7)
c2Δf(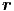 ,t) = c2Δf( ,t) = c2Δf(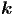 · ·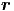 - ωt) - ωt) | = 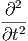 f( f(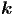 · ·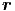 - ωt) = - ωt) = 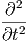 f( f(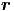 ,t) ,t) | ||
c2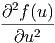 · ·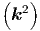 | = 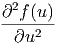 ·ω2 ·ω2 | ||
c2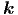 2 = c2 2 = c2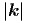 2 2 | = ω2 | (6.8) |
Damit können wir sagen:
 Lizenzinformationen
Lizenzinformationen