 Versuch zur Vorlesung: Lecherleitung (Versuchskarte
SW025)
Versuch zur Vorlesung: Lecherleitung (Versuchskarte
SW025)

Wir untersuchen die Wellenphänomene an 3 Testsystemen,
 Versuch zur Vorlesung: Lecherleitung (Versuchskarte
SW025)
Versuch zur Vorlesung: Lecherleitung (Versuchskarte
SW025)
 Versuch zur Vorlesung: Koaxialleitung (Versuchskarte
SW085)
Versuch zur Vorlesung: Koaxialleitung (Versuchskarte
SW085)
Wenn man das Doppelleitersystem mit elektromagnetischen Wellen mit einer Wellenlänge von etwa λ = 1m speist, beobachtet man folgendes
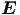 - und
des
- und
des 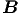 -Feldes in Richtung ℓ. Der Abstand der Intensitätsmaxima beträgt λ∕2
für beide Felder. Die Maxima der
-Feldes in Richtung ℓ. Der Abstand der Intensitätsmaxima beträgt λ∕2
für beide Felder. Die Maxima der  E-Feldes sind gegen denen des
E-Feldes sind gegen denen des 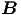 -Feldes
verschoben. Wir haben stehende Wellen.
-Feldes
verschoben. Wir haben stehende Wellen.
 und
und  sind analog wie beim Kondensator.
sind analog wie beim Kondensator.


| Ansicht von oben | Ansicht von unten |
| Bestückungsseite | Seite mit Wellenleitern |
800 MHz-Breitbandverstärker für Fernsehsignale. Auf der Unterseite sind die Wellenleiterstrukturen sichtbar (Mittlere Struktur in Abbildung 6.3)
Abbildung 6.3 zeigt beispielshaft eine Hochfrequenzschaltung. Die Wellenlänge der verstärkten Signale ist zwar einiges grösser als die Schaltung. Die auf der Unterseite sichtbaren Wellenleiterstrukturen verhindern eine unkontrollierte Abstrahlung elektromagnetischer Energie.
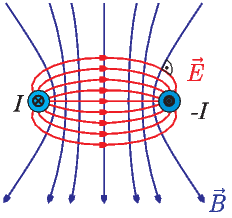
Magnetfelder und elektrische Felder bei einer Lecherleitung.
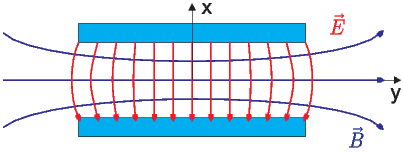
Magnetfelder und elektrische Felder bei einer Doppelleitung aus parallelen Platten
 Materialien
Materialien
Folien zur Vorlesung vom 09. 07. 2009: PDF
Aufgabenblatt 13 für das Seminar vom 15. 07. 2009 (Ausgabedatum 09. 07. 2009):
(HTML oder PDF)
Wir setzen für die 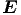 -Welle in der Geometrie der obigen Zeichnung an
-Welle in der Geometrie der obigen Zeichnung an
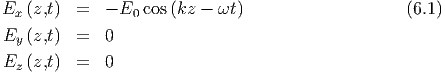
 -Feld durch
-Feld durch
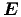 = -(∂∕∂t)
= -(∂∕∂t)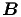 in Komponenten
in Komponenten
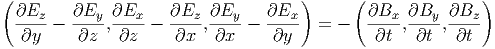 | (6.3) |
Die x- und die z-Komponenten sind null, nach der Voraussetzung. Die y-Komponente lautet
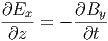 | (6.4) |
Mit c = ω∕k ist diese Kopplungsgleichung, die zweite Maxwellgleichung erfüllt. Die vierte Maxwellgleichung ist ebenfalls erfüllt. Aus ihr erhält man
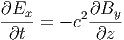 | (6.5) |
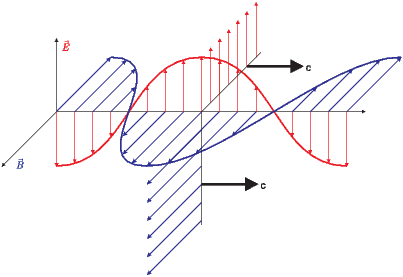
Ausbreitung von elektromagnetischen Wellen
Diese elektromagnetischen Wellen im Innenraum zwischen den beiden Leitern müssen auch in den angrenzenden Leitern Ladungswellen und Stromwellen erzeugen, die mit den Maxwellgleichungen kompatibel sind. Für die Ladungen gilt mit der ersten Maxwellschen Gleichung für die Oberflächenladungsdichte
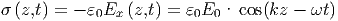 | (6.6) |
Die Oberflächenladungsdichte ist eine fortlaufende Welle. Die Erhaltung der elektrischen Ladung bedingt für die Oberflächenladungsdichte in einem Abschnitt der Breite b
![∂σ (z,t)
b· [j (z + dz,t) - j (z,t)] = -------·b ·dz
∂t](el-20131537x.png) | (6.7) |
und damit
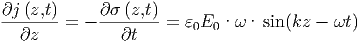 | (6.8) |
Die Integration über z und die Verwendung von c = ω∕k ergibt
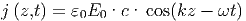 | (6.9) |
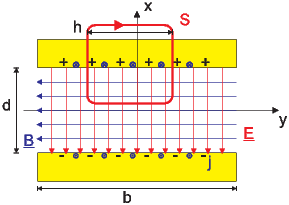
Integrationspfad zur Anwendung des vierten Maxwellschen Gesetzes
Mit dem vierten Maxwellschen Gesetz ∮
S ·d
·d =
= 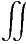 A(S) μ0
A(S) μ0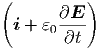 ·d
·d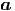 erhalten
wir mit dem eingezeichneten Integrationsweg, da der Term mit
erhalten
wir mit dem eingezeichneten Integrationsweg, da der Term mit 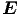 keinen Beitrag gibt
(er liegt in der Integrationsebene)
keinen Beitrag gibt
(er liegt in der Integrationsebene)
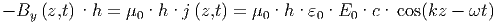 | (6.10) |
Mit ε0·μ0 = 1∕c2 folgt
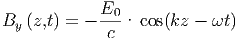 | (6.11) |
eine identische Gleichung zu der im Zwischenraum abgeleiteten. Die Lösung für die auf dem Zweileitersystem transportierten Wellen ist also kompatibel mit den Maxwellgleichungen. Ladungen und Ströme bewegen sich als Wellen auf der Innenseite der Leiter.
Durch die in Abschnitt 6.3 abgeleiteten Gleichungen sind an jedem Ort z entlang des Doppelleitersystems und zu jeder Zeit t die lokal fliessenden Ströme I(z,t) und die elektromotorische Kraft (Spannung) UEMK(z,t) gegeben. Wenn wir nun an einer festen Stelle z in Gedanken einen ohmschen Widerstand zwischen den beiden Leitern einfügen, so muss dieser Widerstand einen vom Wellenleitersystem gegeben Wert haben, dass die elektromotorische Kraft UEMK(z,t) genau den Strom I(z,t) durch den Widerstand treibt. UEMK und I sind dabei von der Wellengleichung gegeben. Nur wenn der Widerstand angepasst ist, also wenn
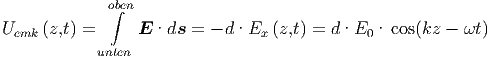 | (6.12) |
gilt, wird aller Strom verbraucht. In allen anderen Fällen bleibt Strom übrig, der an der Stelle reflektiert werden kann, oder die elektromotorische Kraft treibt zusätzlichen Strom durch den Widerstand: dieser wird mit umgekehrtem Vorzeichen reflektiert.
Der gesamte Oberflächenstrom auf der oberen Platte an der Stelle z ist
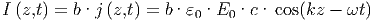 | (6.13) |
Wenn man an einer beliebigen Stelle das Doppelleitersystem entzweischneidet und dort den Widerstand
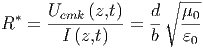 | (6.14) |
den Wellenwiderstand, anschliesst, gibt es einen reflexionsfreien Abschluss, wir haben eine reine fortlaufende Welle. Das gleiche gilt für jede beliebige fortlaufende Welle, auch wenn sie nicht harmonisch ist.
Das Zweidraht-Doppelleitersystem hat den Wellenwiderstand
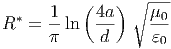 | (6.15) |
Die Grösse
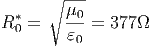 | (6.16) |
ist der Wellenwiderstand des Vakuums.
Stehende Wellen werden aus zwei fortlaufenden Wellen mit entgegengesetztem Wellenvektor
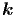 zusammengesetzt. Dabei müssen
zusammengesetzt. Dabei müssen 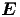 ,
, 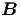 und
und 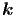 in dieser Reihenfolge ein Rechtssystem
bilden1 .
Die nach rechts laufende Welle wurde schon berechnet (hier sind nur die von null
verschiedenen Komponenten angegeben)
in dieser Reihenfolge ein Rechtssystem
bilden1 .
Die nach rechts laufende Welle wurde schon berechnet (hier sind nur die von null
verschiedenen Komponenten angegeben)
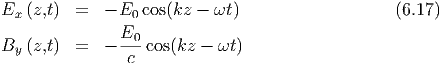
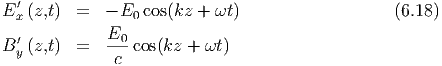
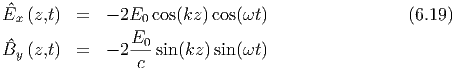
| Im Gegensatz zu laufenden Wellen sind bei stehenden Wellen die
Maxima der 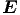 - Felder und der - Felder und der 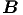 -Felder gegeneinander um λ∕4
verschoben. -Felder gegeneinander um λ∕4
verschoben. |
 Lizenzinformationen
Lizenzinformationen