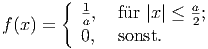

Die Diracsche Deltafunktion ist ein nützliches Instrument, um diskrete Ladungsverteilungen, Kräfte, Punktmassen als kontinuierliche Verteilung oder Kraftfelder zu beschreiben.
Wir beginnen, indem wir die Funktion
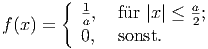 | (C.1) |
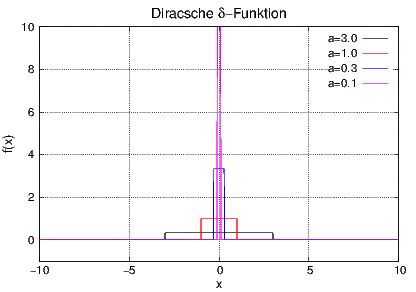
Darstellung von f(x), wobei a variiert wird.
In der Abbildung C.1 sieht man, dass mit kleiner werdendem a die Amplitude von f(x) immer grösser wird. Die Fläche unter der Kurve
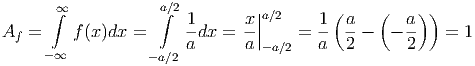 | (C.2) |
ist konstant und unabhängig von a. Wir definieren nun die Diracsche Delta-Funktion
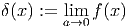 | (C.3) |
Damit ist auch
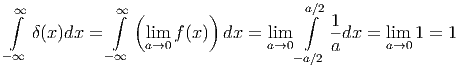 | (C.4) |
Als Anwendung betrachten wir das Integral des Produktes
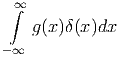 |
wobei g(x) genügend oft (Fragen Sie einen Mathematiker oder lesen die Packungsbeilage oder ein Mathematikbuch) stetig differenzierbar sein soll. Die Taylorreihe von g(x) ist dann
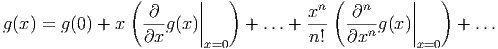 | (C.5) |
Dann ergibt das Integral
| ∫ -∞∞g(x)δ(x)dx | = lim a→0 ∫ -∞∞g(x)f(x)dx | (C.6) | |
= lim a→0 ∫
-∞∞![[ ( | ) ]
∂ ||
g(0) + x ---g(x)|| + ...
∂x x=0](el-20132154x.png) f(x)dx f(x)dx | |||
= lim a→0 ∫
-a∕2a∕2![[ ( | ) ]
∂-- ||
g (0) + x ∂x g(x)|| + ...
x=0](el-20132155x.png) 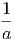 dx dx | |||
= lim a→0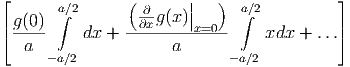 | |||
= g(0) + lim a→0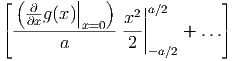 | |||
= g(0) + lim a→0![|
[( ∂ || ) a2 ]
---g(x)|| ---+ ...
∂x x=0 4a](el-20132159x.png) = g(0) = g(0) |
Damit ist klar, dass die nützliche Gleichung
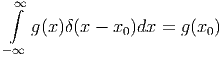 | (C.7) |
gilt. Man kann sie anwenden, zum Beispiel im Gaussschen Gesetz, wenn man das elektrische Feld einer Ebene berechnen will. Wir setzen für die Ladungsdichte
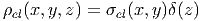 |
Für die Einheiten haben wir
![[ρel] = Cm -3 [σel] = Cm -2](el-20132162x.png) |
Der Unterschied in den Dimensionen rührt daher, dass die Delta-Funktion δ(z)
implizit die Dimension ![[δ(z)]](el-20132163x.png) = m-1 hat, sonst wären die Definition in Gleichung (C.3)
und Gleichung (C.1) dimensionsmässig nicht korrekt.
= m-1 hat, sonst wären die Definition in Gleichung (C.3)
und Gleichung (C.1) dimensionsmässig nicht korrekt.
Das Gausssche Gesetz sagt dann
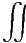 A(V ) A(V ) d d | = 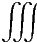 V ρeldV V ρeldV | = | 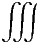 V ρel(x,y,z)dxdydz V ρel(x,y,z)dxdydz | ||||
= 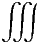 V σel(x,y)δ(z)dxdydz V σel(x,y)δ(z)dxdydz | = | 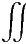 Ebeneσel(x,y)dxdy Ebeneσel(x,y)dxdy |
 Lizenzinformationen
Lizenzinformationen